- Числовые функции. Определение и способы задания
- Урок 1. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Числовые функции. Определение и способы задания»
- Числовые функции. Определение и способы задания
- Урок 1. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Числовые функции. Определение и способы задания»
- Видеоурок »Определение и способы задания числовой функции»
- Конспект урока на тему: «Определение числовой функции и способы ее задания».
Числовые функции. Определение и способы задания
Урок 1. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые функции. Определение и способы задания»
· повторить определение числовых функций;
· повторить способы задания функций;
· повторить основные преобразования графиков числовых функций;
· повторить вид графиков основных функций.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости 
отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.
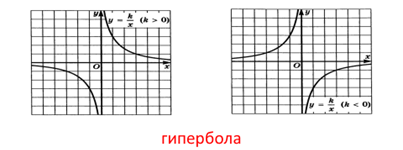
Перед вами графики некоторых функций и их названия.
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок
Источник
Числовые функции. Определение и способы задания
Урок 1. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые функции. Определение и способы задания»
· повторить определение числовых функций;
· повторить способы задания функций;
· повторить основные преобразования графиков числовых функций;
· повторить вид графиков основных функций.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.
Перед вами графики некоторых функций и их названия.
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок
Источник
Видеоурок »Определение и способы задания числовой функции»
Определение числовой функцииПодробнее
Функция числового аргумента. Область определения. Множество значений. Вариант 1Подробнее
Функция и способы ее задания. Преобразовния графиков функций. Преподаватель математики Усенова З.Т.Подробнее
Способы задания функции. 10 класс.Подробнее
01 Числовые функции Определение и способы заданияПодробнее
1 Определение и способы задания числовой функцииПодробнее
ФУНКЦИЯ. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ. ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ. Видеоурок | АЛГЕБРА 7 классПодробнее
10 класс — Алгебра — Определение числовой функции и способы её заданияПодробнее
10 класс/ §1.Понятие функции и способы ее заданияПодробнее
АЛГЕБРА 10 класс: Числовые функции | Короткий видеоурокПодробнее
Алгебра 9 класс (Урок№1 — Функция. Область определения функции)Подробнее
10 класс, 37 урок, Числовые последовательностиПодробнее
10 класс, 7 урок, Определение числовой функции и способы её заданияПодробнее
Определение и задание обратной числовой функции | Алгебра 10 класс #6 | ИнфоурокПодробнее
Определение и способы задания числовой функции | Алгебра 10 класс #1 | ИнфоурокПодробнее
9 класс, 16 урок, Способы задания функцииПодробнее
9 класс, 15 урок, Определение числовой функции. Область определения, область значений функцииПодробнее
М10 (7.1-7.28) Функция. Способ задания функции.Подробнее
Источник
Конспект урока на тему: «Определение числовой функции и способы ее задания».
Конспект урока на тему: « Определение числовой функции и способы ее задания ».
Предмет: алгебра. 10 класс.
Автор: учитель математики МКОУ «Цухтамахинская СОШ».
Нугаева Хамис Магомедовна.
Цель: обсудить определение функции, способы ее задания.
I. Сообщение темы и цели уроков
II. Повторение материала 9 класса
Различные аспекты этой темы уже рассматривались в 7-9 классах. Теперь необходимо расширить и обобщить сведения о функциях. Напомним, что тема является одной из важнейших для всего курса математики. Различные функции будут изучаться вплоть до окончания школы и далее в высших учебных заведениях. Данная тема вплотную связана с решением уравнений, неравенств, текстовыми задачами, прогрессиями и т. д.
Определение 1. Пусть даны два множества действительных чисел D и Е и указан закон f по которому каждому числу х ∈ D ставится в соответствие единственное числом y ∈ Е (см. рисунок). Тогда говорят, что задана функция у = f ( x ) или у(х) с областью определения (О.О.) D и областью изменения (О.И.) Е. При этом величину х называют независимой переменной (или аргументом функции), величину у — зависимой переменной (или значением функции).
Область определения функции f обозначают D ( f ). Множество, состоящее из всех чисел f ( x ) (область значений функции f ), обозначают E ( f ).
Рассмотрим функцию 
Для нахождения у для каждого значения х необходимо выполнить следующие операции: из величины х вычесть число 2 (х — 2), извлечь квадратный корень из этого выражения 
и, наконец, прибавить число 3 
Совокупность этих операций (или закон, по которому для каждого значения х ищется величина у) и называется функцией у(х). Например, для х = 6 находим 
Таким образом, для вычисления функции у в данной точке х необходимо подставить эту величину х в данную функцию у(х).
Очевидно, что для данной функции для любого допустимого числа х можно найти только одно значение у (т. е. каждому значению х соответствует одно значение у).
Рассмотрим теперь область определения и область изменения этой функции. Извлечь квадратный корень из выражения (х — 2) можно, только если эта величина неотрицательная, т. е. х — 2 ≥ 0 или х ≥ 2. Находим 
Так как по определению арифметического корня 
то прибавим ко всем частям этого неравенства число 3, получим: 
или 3 ≤ у 
В математике часто используются рациональные функции. При этом функции вида f ( x ) = р(х) (где р(х) — многочлен) называют целыми рациональными функциями. Функции вида 
(где р(х) и q ( x ) — многочлены) называют дробно-рациональными функциями. Очевидно, дробь 
определена, если знаменатель q ( x ) не обращается в нуль. Поэтому область определения дробно-рациональной функции 
— множество всех действительных чисел, из которого исключены корни многочлена q ( x ).
Рациональная функция 
определена при х — 2 ≠ 0, т. е. x ≠ 2. Поэтому область определения данной функции — множество всех не равных 2 действительных чисел, т. е. объединение интервалов (-∞; 2) и (2; ∞).
Напомним, что объединением множеств А и В называется множество, состоящее из всех элементов, входящих хотя бы в одно из множеств А или В. Объединение множеств А к В обозначается символом А U В. Так, объединением отрезков [1; 5] и (3; 9) является промежуток [1; 9). Объединение промежутков [1; 2) и [3; 4] (непересекающиеся промежутки) обозначают [1; 2) U [3; 4].
Возвращаясь к примеру, можно записать: 
Так как при всех допустимых значениях х дробь 
не обращается в нуль, то функция f ( x ) принимает все значения, кроме 3. Поэтому 
Найдем область определения дробно-рациональной функции 
Знаменатели дробей обращаются в нуль при х = 2, х = 1 и х = -3. Поэтому область определения данной функции 
Зависимость 
уже не является функцией. Действительно, если мы хотим вычислить значение у, например, для х = 1, то, пользуясь верхней формулой, найдем: у = 2 · 1 — 3 = -1, а пользуясь нижней формулой, получим: у = 12 + 1 = 2. Таким образом, одному значению x ( x = 1) соответствуют два значения у (у = -1 и у = 2). Поэтому эта зависимость (по определению) не является функцией.
Приведены графики двух зависимостей y ( x ). Определим, какая из них является функцией.
На рис. а приведен график функции, так как любой точке x 0 соответствует только одно значение у0. На рис. б приведен график какой- то зависимости (но не функции), так как существуют такие точки (например, x 0), которым отвечает более одного значения у (например, у1 и у2).
Рассмотрим теперь основные способы задания функций.
1) Аналитический (с помощью формулы или формул).
Рассмотрим функции: 
Несмотря на непривычную форму, это соотношение также задает функцию. Для любого значения х легко найти величину у. Например, для х = -0,37 (так как х 0, то пользуемся нижним выражением) имеем: 
Из способа нахождения у понятно, что любой величине х отвечает только одно значение у.
в) 3х + у = 2у — х2. Выразим из этого соотношения величину у: 3х + х2 = 2у — у или х2 + 3х = у. Таким образом, это соотношение также задает функцию у = х2 + 3х.
Источник
