- ГДЗ Алгебра Самостоятельные работы за 10 класс Александрова Базовый уровень Мнемозина (к учебнику Мордкович)
- ГДЗ по алгебре Самостоятельные работы за 10 класс Александрова Базовый уровень к учебнику Мордкович
- Числовые функции. Определение и способы задания
- Урок 1. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Числовые функции. Определение и способы задания»
- Сборник самостоятельных работ по алгебре(10 класс)
ГДЗ Алгебра Самостоятельные работы за 10 класс Александрова Базовый уровень Мнемозина (к учебнику Мордкович)
Алгебра в 10 классе имеет свои трудности, которые он должен преодолеть как можно скорее. Эти проблемы касаются не только правил, формул, но и умения мыслить и понимать задачи. А это умение, как известно, является одной из самых сложных способностей человека. Выполнение самостоятельной работы по алгебре ставит перед десятиклассником ряд личностно – значимых проблем, которые позволяют понять самому, как решать задачи. Это не просто подготовка к работе на уроке по шаблону, но и самостоятельное создание ситуации успеха, которая должна стать нормой для каждого ученика. Только в этом случае, любой десятиклассник сможет найти возможность проявить свои способности, почувствовать, что он чего – то может достичь самостоятельно. Проверить правильность выполненных решений можно с помощью ГДЗ по алгебре и начала математического анализа Александрова Л.А., которое полностью соответствует всем требованиям школьной программы основного среднего образования и федеральному государственному общеобразовательному стандарту.
Сформировать умения применять свои знания на практике в различных ситуациях и разных предметных областях является одной из главных задач обучения. Освоение знаний – это только половина дела. Главное это иметь большое желание учиться, быть любознательным, а так же уметь добывать эти знания, пользоваться ими в определенной ситуации, такого требования общеобразовательного стандарта.
Одной из основных причин неспособность школьника применять математические знания в практической работе является отсутствие или недостаток знаний об общих закономерностях, умение осуществлять выбор способа решения в конкретной ситуации, а так же и опыта применения математики для решения задач в смежных предметах. Овладеть школьником методов решения задач повышает его уровень математического развития. Математический язык относится к числу наиболее распространенных языков. Он широко используется в литературе, в печати, в научно – технических и практических публикациях. Благодаря этому и язык математики получил широкое применение в других научных дисциплинах. Язык математики имеет свои законы развития, что объясняется её природой. В языке математики можно выделить две основные составляющие: – это естественный язык (его ещё называют языком логики), на котором принято выражать мысли, и символы, которыми изображаются эти мысли. Именно при обучении алгебры в школе ставится задача овладеть символьным языком алгебры, это и позволит ученику глубже разобраться в математических моделях, что в свою очередь позволит в дальнейшем более полно использовать математический аппарат в экономических расчетах. Для этого в качестве объектов исследования были выбраны некоторые элементы математического аппарата алгебры, такие как определители, матрица, вектор, операции, сложение и так далее. Необходимость изучения комплекс чисел в курсе алгебры и начала математического анализа обуславливается потребностью в математических моделях многих физических явлений. В настоящее время одним из основных направлений развития теории дифференциальных уравнений является её приложение к задачам механики сплошных сред. Это направление связано с созданием теории одномерных и двумерных уравнений математической физики, где на первый план выходят задачи о фазовых переходах. Для решения таких задач необходимо знание свойств интегральных представлений функции, имеющие множество точек разрыва.
ГДЗ по алгебре Самостоятельные работы за 10 класс Александрова Базовый уровень к учебнику Мордкович
Курс алгебры и начала математического анализа является основой для получения фундаментальных знаний в областях, непосредственно примыкающих к школьной программе и для продолжения образования в технических, экономических и гуманитарных в высших учебных заведениях. К тому же курс алгебры и начала математического анализа является завершающим этапом в школьном обучении математики. Этот курс имеет большую практическую значимость, что связано с формированием и развитием ряда умений и навыков. При изучении этой дисциплины у десятиклассника вырабатываются навыки работы с тестовыми заданиями. Ученик учится самостоятельно работать, наблюдать, обобщать, делать выводы, применять теоретические знания на практике. Умения и навыки формируются в процессе решения примеров и задач. Для этого отлично подойдет использование ГДЗ по алгебре и начала математического анализа 10 класс Александрова Л.А., который поможет глубже вникнуть в систему понятий, необходимых для решения задач, входящих в школьный курс элементарной математики. В нем отражены все темы учебника такие как:
- числовые функции,
- тригонометрические функции и уравнения,
- преобразование тригонометрических выражений,
- производная.
Решебник является можно сказать, что по сути своей он выполняет функции репетитора по алгебре. Он содержит в себе не только решения простых примеров и задач, но и более сложных. Пользоваться онлайн – решебником можно в любое, удобное для школьника, время и в любом месте, где имеется выход в Интернет, хоть с компьютера, хоть с любого электронного устройства. С его помощью каждый ученик сможет:
- получить полное качественное выполнение домашнего задания,
- провести подготовку, как к самостоятельной работе, так и подготовку к следующему уроку,
- устранить имеющиеся пробелы в знании той или иной темы,
- закрепить знания.
Решебник поможет и родителям проверить, насколько их ребенок знает алгебру.
Его может использовать и учитель математики для проверки домашнего задания, подготовке к самостоятельной работе, а так же как справочное пособие.
Источник
Числовые функции. Определение и способы задания
Урок 1. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые функции. Определение и способы задания»
· повторить определение числовых функций;
· повторить способы задания функций;
· повторить основные преобразования графиков числовых функций;
· повторить вид графиков основных функций.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости 
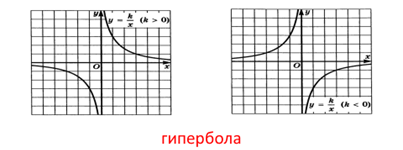
Перед вами графики некоторых функций и их названия.
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок
Источник
Сборник самостоятельных работ по алгебре(10 класс)
Составитель: Болдырева О.В., учитель математики высшей категории
СОШ № 83 им. Г.Мустафина
Рецензент : Раздобреева Л.В., учитель математики высшей категории
СОШ № 83 им. Г.Мустафина
Методическое пособие рассмотрено и одобрено методическим советом Отдела образования города Караганды, протокол № 10 от 30.05.2016г
Предлагаемые самостоятельные работы являются методическими разработками для проведения тематического контроля по алгебре. Методические разработки содержат самостоятельные работы по всем темам курса алгебры 10 класса. Работы состоят из 2 вариантов, по 5-11 заданий в каждом, разбиты на три уровня. Позволяют в течении 15 минут отследить три этапа: знание, понимание и применение..
Предлагаемые самостоятельные окажут помощь учителям математики.
Самостоятельная работа № 1. Функция и способы её задания .…….. .4
Самостоятельная работа № 2. Простейшие преобразования графиков .6
Самостоятельная работа № 3 Свойства функций ……………………… 8
Самостоятельная работа № 4 Основные свойства и графики тригонометрических функций…………………………………………. 10
Самостоятельная работа № 5 Обратные тригонометрические функции………………………… ………………………………………. 12
Самостоятельная работа № 6 Простейшие тригонометрические
уравнения и их решение ..…..…………………………………………. 14
Самостоятельная работа № 7 Способы решения тригонометрических уравнений ………………………………………………………………. 16
Самостоятельная работа № 8 Решение тригонометрических
Самостоятельная работа № 9 Определение производной. Правила нахождения производной ………………………………………………..20
Самостоятельная работа № 10 Производная сложной функции ……22
Самостоятельная работа № 11 Производная тригонометрических и обратных тригонометрических функции ………………………………24
Самостоятельная работа № 12 Признаки возрастания и убывания функции ………………………………………………………………..…26
Самостоятельная работа № 13 Критические точки и экстремумы
Самостоятельная работа № 14 Наибольшее и наименьшее значение функции ………………………..…………………………………………30
Самостоятельная работа № 15 Комбинаторика и бином Ньютона ….32
Математика является базовым школьным предметом, входит в число основных предметов ЕНТ, поэтому качественное усвоение материала школьниками всегда имело и будет иметь большую значимость.
Одна из важнейших целей, стоящих перед школьным учителем, сделать изучение математики успешным, научить использовать полученные знания при выполнении практических заданий, и, наоборот, выполняя практические задания, научиться обобщать результаты и делать выводы. Достижение этой цели невозможно без контроля над усвоением знаний учащихся, без проверки умений и навыков.
Для проведения контроля за знаниями и умениями учащихся сегодня применяется много различных способов. Один из таких способов – самостоятельная работа.
Предлагаемые методические разработки содержат самостоятельные работы по алгебре и началам анализа 10 класса. Цель предлагаемых разработок — оказание помощи учителю при организации проверки и контроля знаний и умений учащихся 10 класса, в процессе изучения курса алгебры и начал анализа по учебнику А.Е. Абылкасымовой, З.А. Жумагуловой, К.Д. Шойынбекова, В.Е. Корчевского «Алгебра и начала анализа».
Самостоятельные работы расположены в порядке изложения теоретического материала в учебнике. Задания предусматривают закрепление теоретических и практических умений учащихся. Каждая работа состоит из двух вариантов по 5 – 11 заданий в каждой, разбита на три уровня.
Уровень А состоит из заданий, позволяющих проверить знание теоретических основ темы, включает тестовые вопросы открытого и закрытого типа.
Уровень В состоит из заданий на понимание и использование теоретических основ при работе с графиками, единичной окружностью, изображением интервалов на числовой прямой и решении простейших заданий. Все задания уровня В являются тестовыми, содержат от 4 до 6 вариантов ответа.
Уровень С практический. Учащиеся должны показать насколько хорошо усвоили тему, решив соответствующие задачи.
Таким образом каждая самостоятельная работа позволяет в течении 15 минут отследить три этапа: знание, понимание и применение.
В зависимости от степени подготовленности учащихся и скорости выполнения заданий, учитель может регулировать время, отведенное на решение, упрощать, заменять и усложнять задания. А также определять процентное соотношение выполненной работы с выставляемой оценкой.
Проводить указанные работы можно на любом этапе урока. Если самостоятельная работа проведена не на заключительном этапе, то рекомендуется проверить и разобрать допущенные ошибки уровней А и В для предотвращения их дальнейшего появления.
Самостоятельная работа № 1.
Тема: Функция и способы её задания
Функция — это зависимость…
а) переменной x от y ; б) при которой каждому значению x соответствует одно или несколько значений y ; в) при которой каждому значению x соответствует единственное значение y ; г) при которой каждому значению y соответствует единственное значение x .
где x — ___________________ , у — ______________________
Область определения функции — это… а) множество значений, которые может принимать аргумент; б) множество значений, которые может принимать функция; в) множество значений x , при которых y = 0; г) множество значений y , при которых x = 0.
Используя обозначения и символы запишите: Множество значений функции f все действительные числа.
Какая из кривых, изображенных на рисунке, не является графиком функции?
Дана функция f ( x ) = . При каком значении аргумента f ( x ) = -24.
Найдите область определения функции
Самостоятельная работа № 1.
Тема: Функция и способы её задания
Функцией нельзя считать зависимость…
а) переменной x от y ; б) при которой каждому значению x соответствует одно или несколько значений y ; в) при которой каждому значению x соответствует единственное значение y ; г) при которой каждому значению y соответствует единственное значение x .
2. Функция задана формулой y = f ( x ) , где ____ — независимая переменная (аргумент) , ____ — зависимая переменная (функция)
3. Множество значений функции — это… а) множество значений, которые может принимать аргумент; б) множество значений, которые может принимать функция; в) множество значений x , при которых y = 0; г) множество значений y , при которых x = 0.
Используя обозначения и символы запишите: Областью определения функции являются все неотрицательные числа.
Какая из кривых, изображенных на рисунке, является графиком функции?
Из данных функций выберите те, множеством значений которых является промежуток (
Дана функция f ( x ) = . При каком значении аргумента f ( x ) = — 4,8.
Найдите область определения функции
Самостоятельная работа № 2.
Тема: Простейшие преобразования графиков
Что из перечисленного является преобразование графика функции: а) параллельный перенос; б) симметрия относительно оси Ох; в) сжатие вдоль оси Ох; г) гомотетия.
График функции y = f ( x ) + d получается из графика функции y = f ( x ) путем: а) растяжения на d единиц к оси Ох; б) параллельного переноса вдоль оси Ох на | d | единиц в положительном направлении при d d > 0; в) параллельного переноса вдоль оси Оу на | d | единиц в положительном направлении при d >0 и в отрицательном направлении, если d 0; г) путем сжатия в d раз к оси Ох
На каком графике изображено преобразование графика у = 3х в у = 3(х + 1)
График функции у = 2(х – 1) 2 + 5 получается из графика функции у= .. . путем: 1) параллельного переноса вдоль оси Ох на____единиц в _______направлении; 2) растяжением вдоль оси Оу в _____раза; 3) параллельного переноса на ______единиц вдоль оси Оу в ______направлении.
Постройте график функции у = х 2 + 4х + 3, описав алгоритм преобразования из графика функции у = х 2
Источник