- Числовые функции. Определение и способы задания
- Урок 1. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Числовые функции. Определение и способы задания»
- Числовые функции. Определение и способы задания презентация к уроку по алгебре (10 класс) на тему
- Презентация к уроку математики 10 класса. Числовые функции. Определение и способы задания.
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- Определение функции. Способы задания функции.
- Способы задания функции.
- Аналитический способ задания функции.
- Графический способ задания функции.
- Табличный способ задания функции.
- Презентация по математике для 10 класса «Числовые функции»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Числовые функции. Определение и способы задания
Урок 1. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые функции. Определение и способы задания»
· повторить определение числовых функций;
· повторить способы задания функций;
· повторить основные преобразования графиков числовых функций;
· повторить вид графиков основных функций.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости 
Перед вами графики некоторых функций и их названия.
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок
Источник
Числовые функции. Определение и способы задания
презентация к уроку по алгебре (10 класс) на тему
Презентация к уроку математики 10 класса. Числовые функции. Определение и способы задания.
Скачать:
| Вложение | Размер |
|---|---|
| 01._chislovye_funktsii._opredelenie_i_sposoby_zadaniya.pptx | 2.49 МБ |
Предварительный просмотр:
Подписи к слайдам:
Числовые функции. Определение и способы задания.
Напомним Если даны числовое множество и правило , позволяющее поставить в соответствие каждому элементу из множества определенное число , то говорят, что задана функция с областью определения : – область определения функции; – независимая переменная или аргумент; – зависимая переменная; множество всех значений , называют областью значений функции и обозначают .
Если дана функция , и на координатной плоскости отмечены все точки вида , где , а , то множество этих точек называют графиком функции , .
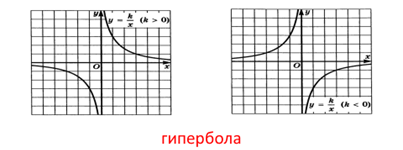
Графики некоторых функций прямая
Зная график функции с помощью геометрических преобразований можно построить график функции . Для этого надо сделать параллельный перенос графика функции на вектор , то есть на вправо, если , и влево, если на вверх, если , и вниз, если .
Пример -4 0 1 2 3 4
Задать функцию – указать правило , которое поз- воляет по произвольно выбранному значению вычислить соответствующее значение . Чаще всего это правило связано с формулой (например ). Такой способ задания функции называется аналитическим .
Пример Пусть – некоторая линия на координатной плоскости
Тем самым на отрезке задана функция . Такой способ задания функции называют графическим . Заметим, что если функция была задана аналитически и нам удалось построить ее график, то тем самым мы фактически осуществили переход от аналитического способа задания функции к графическому.
Табличный способ задания функции – с по-мощью таблицы, в которой указаны значения функции для конечного множества значений аргумента. Например : 5 7 8 9 10 12 5 7 4 6 5 7 8 9 10 12 5 7 4 6
Словесный способ задания функции – способ, при котором правило задания функции описывается словами.
Пример: Функция задана на множестве всех неотрицательных чисел с помощью следующего правила: каждому числу ставится в соответствие первая цифра после запятой в десятичной записи числа . Если , , то 6, так как =0 ,(6) то , так как
По теме: методические разработки, презентации и конспекты
Открытый урок. Способы задания числовой функции.
Цели урока: 1. Образовательная: продолжить формирование умений и навыков работы с числовыми функциями:Навыков задания функций различными способами;Навыков перехода от одного способа задания функ.
Конспект урока математики (по новым ФГОС), по теме:Понятие функции. Область определения и множество значений функции. Способы задания функции.
Конспект урока математики по новым ФГОС.Тема урока: Понятие функции. Область определения и множество значений функции. Способы задания функции.
«Определение числовой функции. Область определения и область значений функции»
Уточнить понятие функции, её основных характеристик — области определения и области (множества) значений.
«Определение числовой функции. Область определения и область значений функции» Урок математики Корниенко Анны Михайловны МБОУ СОШ № 9 Староминская
Уточнить понятие функции, её основных характеристик — области определения и области (множества) значений.
Определение числовой функции. Область определения, область значений функции.
презентация к уроку.
Урок алгебры в 9 классе «Определение числовой функции. Область определения и область значений функции»
Урок «Определение числовой функции. Область определения и область значений функции» по учебнику А. Г. Мордковича. Тип урока: обобщение и систематизация знанийЗадачи: создать усл.
Источник
Определение функции. Способы задания функции.
Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?
Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.
Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.
Способы задания функции.
В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.
Аналитический способ задания функции.
Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.
Примеры аналитического задания функции:
Графический способ задания функции.
Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.
Примеры, графического задания функции:


 Табличный способ задания функции.
Табличный способ задания функции.
Следующий способ задания функции применяется чаще всего на практике называется табличный.
Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.
Примеры, табличного задания функции:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
Рассмотрим примеры по теме «Способы задания функции»:
Пример №1:
Является ли графическим заданием какой-либо функции фигура?


Является ли графическим заданием какой-либо функции фигура?
Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Является ли графическим заданием какой-либо функции фигура?

Источник
Презентация по математике для 10 класса «Числовые функции»
Описание презентации по отдельным слайдам:
Числовые функции Установить соответствие и задать функцию означает одно и тоже. Маркушевич А. И Урок разработан учителем математики МБОУ «СОШ №34», г. Бийска Алтайского края Масловой Светланой Константиновной, при участии учащихся 10 класса (Пановой В, Галкиной А, Ралдугина И, Хисамутдинова А)
«Определение числовой функции и способы её задания» Учащийся 10 класса Хисамутдинов А
Определение 1 Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу х из множества Х определённое число у, то говорят, что задана функция у = f (x) с областью определения Х. Область определения функции обозначают D (f). Множество всех значений функций у = f (x), х є Х называют областью значений функции и обозначают E (f). Учащийся 10 класса Хисамутдинов А
Способы задания функции. Аналитический. Графический. Табличный. Учащийся 10 класса Хисамутдинов А
Определение 2 Если дана функция у = f (x), x принадлежит Х и на координатной плоскости х О у отмечены все точки вида (х ; у), где х принадлежит Х, а у = f (x), то множество этих точек называют графиком функции у = f (x), x принадлежит Х. Учащийся 10 класса Хисамутдинов А
Пример Построить график функции Решение. Учащийся 10 класса Хисамутдинов А
№1. Выясните, на каком рисунке указаны графики функций y=f(x). Укажите область определения и область значения этих функций (за единицу масштаба принять размер одной клетки). Ответ: a) D(f)=(-3;3], E(f)=(-1;3], в) D(f)=[-1; +∞), E(f)=[-2; +∞). Урок учителя математики Масловой С. К.
№2. Найдите область определения функций Ответ: [12; +∞) Ответ: [-12;-1)U(-1;1) U(1; +∞) Урок учителя математики Масловой С. К.
Учащаяся 10 класса Панова В
1. D (f) = [-4; +∞) 2. E (f) = [ 0; +∞) 3. у= 0, при х = -4 4. у> 0, при х є ( -4; +∞) 5. Возрастает при х є [-4; 0] u [3;+∞) Убывает при х є [ 0; 3] 6. унаиб — не существует, унаим = 0 7. Функция ни четная и ни нечетная 8. уmax=4 , уmin= 1 9. Функция не периодическая 10. Функция ограничена снизу 11. Функция непрерывна 12. Функция выпукла вверх при х є [-4;0], функция выпукла вниз при х є [ 0; 3] 13. Асимптот нет. Учащаяся 10 класса Панова В
Ответ: б). №3. Укажите график нечетной функции Урок учителя математики Масловой С. К.
Периодические функции. Функцию, имеющую отличный от нуля период Т, называют переодической. Если функция у = f(х), хХ имеет период Т, то любое число, кратное Т(т.е. число вида kТ, kєZ), также является её периодом. выполняются равенства: f(х — Т) = f(х) = f(х + Т) Учащаяся 10 класса Галкина А
Пример. Доказать, что функция у = <х>– периодическая. Решение. Числа х и х ± k, где k – любое целое число, имеет одинаковую дробную часть, т. е. <х - k>= <х>= <х + k>. Значит, любое целое число является периодом функции; есть и основной период: Т = 1. Учащаяся 10 класса Галкина А
№4. Постройте график периодической функции f(x)=ІxІ с периодом 2 на отрезке [-1;1]. Укажите её свойства. Урок учителя математики Масловой С. К.
Учащийся 10 класса Ралдугин И
Учащийся 10 класса Ралдугин И
Если функция y=f(x) монотонна на множестве X, то она обратима. Учащийся 10 класса Ралдугин И
Показать ,что для функции y=5x-3 существует обратная функция ,и найти её аналитическое выражение. Решение. Линейная функция Y=5X-3 определена на R,возрастает на R и область её значений есть R. Значит , обратная функция существует на R. Чтобы найти её аналитическое выражение ,решим уравнение Y=5X-3 относительно x; получим:X=(y+3)/5.Это и есть искомая обратная функция. Она определена и возрастает на R. Учащийся 10 класса Ралдугин И
№5. Для функции, заданной табличным способом, укажите её область значений и определите имеет ли она обратную функцию? а) б) Ответ: а) нет, б) да. Урок учителя математики Масловой С. К. х 1 2 5 7 У 3 4 7 3 х 1 2 3 7 у 5 8 9 1
№6. у = f(x) и y = g(x) – взаимно-обратные функции, причем f(5) = 8 и g(7) = 1. Решите уравнения f(3x) = 7 и g(5-x) = 5. Ответ: 1/3, -3. Урок учителя математики Масловой С. К.
Ответы к тесту. Вариант 1. Шкала оценок Вариант 2. Урок учителя математики Масловой С. К. № задания 1 2 3 4 5 6 7 Прав. ответ 2 3 2 3 1 3 2 № задания 1 2 3 4 5 6 7 Прав. ответ 2 4 3 1 4 3 1 Кол-во ошибок Оценка 0 5 1 4 2-3 3
Домашнее задание. Учебник 10 класса Алгебра и начала анализа (в 2-х частях) А.Г. Мордкович, П.В. Семенов. Глава 2, № 7.29, 8.21, 8.34, 9.28, 10.27 (в), 8.32 (б). Урок учителя математики Масловой С. К.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 807 человек из 76 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 284 человека из 69 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 603 человека из 75 регионов
Ищем педагогов в команду «Инфоурок»
Презентация к уроку математики в 10 классе по теме «Числовые функции», учителя МБОУ «СОШ №34» города Бийска Алтайского края Масловой С.К., составлена совместно с учащимися. Урок носит обобщающий характер и является подготовительным к контрольной работе по данной теме. В уроке использованы элементы самоконтроля и взаимоконтроля, задания из Единого государственного экзамена, в конце урока проводиться небольшое тестирование. Учащиеся повторяют полностью такие подтемы как определение и способы задания числовой функции, обратная и периодическая функции, исследование числовой функции.
Номер материала: 37623032501
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана
Время чтения: 1 минута
Российские школьники завоевали пять медалей на олимпиаде по физике
Время чтения: 1 минута
Российский совет олимпиад школьников намерен усилить требования к олимпиадам
Время чтения: 2 минуты
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
В России выбрали топ-10 вузов по работе со СМИ и контентом
Время чтения: 3 минуты
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
















 Табличный способ задания функции.
Табличный способ задания функции.











