- План конспект урока №1- №2. Алгебра 10 класс. Базовый уровень
- Числовые функции. Определение и способы задания
- Урок 1. Алгебра 10 класс
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Числовые функции. Определение и способы задания»
- Урок алгебры в 10-м классе по теме «Числовые функции. Область определения и множество значений функций»
- Ход урока
- I. Организационный момент.
- II. Повторение.
- III. Изучение нового материала.
- IV. Закрепление.
- V. Итог урока.
- VI. Домашнее задание. Инструктаж по домашнему заданию.
План конспект урока №1- №2. Алгебра 10 класс. Базовый уровень
План конспект урока № 1 – 2 . (1 четверть). Алгебра 10 класс.
Определение числовой функции и способы ее задания.
УМК Мордкович А.Г. Базовый уровень.
Повторить определение функции, область определения, область значений функции
Вспомнить определение графика функции
Разобрать способы определения функции (аналитический, графический, табличный, словесный)
Развитие творческой самостоятельности мышления учащихся.
Решите неравенство а) 
, б) 
В) 
г) 
Определение функции, область определения область значений функции.
Г) постройте график этой функции
Решить упражнения: № 1.1(а, б), №1.2(а, б), № 1.4 – 1.8(а, б)
Самостоятельная работа (найти область определения функции)
№ 1. Дана функция: 
.
Найдите значения х, при которых: а) 
; б) 
; в) 
; г) 
.
№ 2. Найдите область определения функции: 
.
№ 3 .Построить график функции (учебник А9кл. № 11.24, стр.78)
№ 1. Дана функция: 
.
Найдите значения х, при которых: а) ; б) ; в) ; г) .
№ 2. Найдите область определения функции: 
.
№ 3. Построить график функции. (учебник А9кл. № 11.23, стр.78)
Домашнее задание: № 1.1(в), №1.2 (в), №1.4 (в), №1.5 (в, г), №1.6 (в, г) № 1.19, № 2.13
Источник
Числовые функции. Определение и способы задания
Урок 1. Алгебра 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Числовые функции. Определение и способы задания»
· повторить определение числовых функций;
· повторить способы задания функций;
· повторить основные преобразования графиков числовых функций;
· повторить вид графиков основных функций.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости 
отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.
Перед вами графики некоторых функций и их названия.
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок
Источник
Урок алгебры в 10-м классе по теме «Числовые функции. Область определения и множество значений функций»
Разделы: Математика
Тип урока: введение нового материала.
Цели урока:
- Ввести и закрепить определения функции, области определения функции и графика функции.
- Обогатить опыт учащихся в получении новых знаний на основе уже имеющихся теоретических знаний, а также через использование знакомых ситуаций практического характера.
- Развивать логическое мышление учащихся через формирование строить графики функций.
- Воспитывать графическую культуру учащихся.
Оборудование: учебное пособие «Алгебра и начала анализа. 10 класс (профильный уровень)» А.Г. Мордкович. Таблицы числовых функций. Презентация к уроку.
План урока:
| № | Этап урока | Цель этапа | Время |
| 1. | Организационный момент | Сообщение темы урока; постановка цели урока; сообщение этапов урока. | 1 мин |
| 2. | Повторение | Повторить ранее изученные функции. | 5 мин |
| 3. | Изучение нового материала | Ввести понятие функции; области определения функции; области значений функции; определение графика функции. | 15 мин |
| 4. | Закрепление изученного материала | Первичное закрепление полученных знаний. | 14 мин |
| 5. | Итог урока | Обобщение знаний, полученных на уроке. | 3 мин |
| 6. | Домашнее задание | Инструктаж по домашнему заданию. | 2 мин |
Ход урока
I. Организационный момент.
Учитель сообщает учащимся цель урока и средства ее достижения.
II. Повторение.
В различных сферах жизни мы нередко имеем дело со всевозможными соответствиями, т.е. правилами, по которым одним объектам (элементам) сопоставляются другие. Вот некоторые примеры таких соответствий.
Все эти соответствия можно разделить на группы по различным признакам. Но есть среди них совершенно особенные, такие как 1, 2 и 5. Это такие соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества. Такие соответствия и называются функциями.
III. Изучение нового материала.
| Задания и вопросы учителя | Предполагаемые ответы учащихся |
| Что же такое функция? | Определение 1. Если даны числовое множество Х и правило f , позволяющее поставить в соответствие каждому элементу х из множества Х определенное число у, то говорят, что задана функция у =f (х) с областью определения Х. |
| Как записывают? | Пишут : у = f(х), х Є Х. |
| Как обозначают область определения? | Для области определения функции используют обозначение D (f). |
| Как обозначают множество значений? | Множество всех значений функции у = f (x) называют областью значений функции и обозначают E (f). |
| Как называют переменную х ? | Х – независимая переменная или аргумент. |
| Как называют переменную у ? | У – зависимая переменная. |
Найдите область определения функций:
|
|
| Вычислите значения данных функций в точках 1 и 4. |
|
| Что такое график функции? | Определение 2. Если дана функция у = f(x) , хЄХ и на координатной плоскости хОу отмечены все точки вида (х; у), где х Є Х, а у = f (x), то множество этих точек называют графиком функции. |
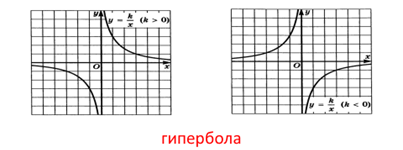
Как выглядят графики некоторых функций?
|
|
IV. Закрепление.
Дана функция у = f(х), где
- Вычислить:
а) f( -2);
б) f ( 0);
в) f( 1, 25);
г) f(6). - Найти D (f) и E(f).
- Выяснить, сколько корней имеет уравнение f(х) =а при различных значениях а.
- Решить неравенства:
а) f(х) 0,5.
Решение.
Дана кусочная функция.
1.
а) значение х=-2 удовлетворяет условию -2 ≤ х ≤ 0, значит f( -2) надо вычислять по формуле f(х) =- х²; f( -2) = -(-2)² ==-4.
б) значение х =0 удовлетворяет условию -2 ≤ х ≤ 0, значит f ( 0) надо вычислять по формуле f(х) =- х²; f ( 0) =-0² =0.
в) значение f( 1, 25) удовлетворяет условию 0 3, значит f(6) надо вычислять по формуле 3/х +1
2. Область определения D (f) состоит из трех промежутков: [-2;0], (0;3], (3; +∞). Объединив их, получим луч [-2; +∞).
Чтобы найти область значений функции, построим ее график. Он состоит из трех кусочков заданной функции. Спроецировав этот график на ось у, получим область значений функции.
3. Выясним, сколько корней имеет уравнение f(х) =а при различных значениях а.
Для этого нужно определить, сколько точек пересечения имеет построенный график функции с прямой у=а при различных значениях параметра а.
- При -4 ≤ а≤ 0 прямая пересекается с графиком в одной точке. Значит, уравнение имеет 1 корень.
- При а 2 корней нет.
- При а=2 – 1 корень.
- При 1 0,5 при х>0.
V. Итог урока.
- Какое соответствие называется функцией?
- Что такое область определения Х функции?
- Дайте определение графика функции.
VI. Домашнее задание. Инструктаж по домашнему заданию.
§7. № 7.12 (а,б); 7.13(а,б); 7.23; 7.24.
Источник
