Опишите способ замены плоскостей проекций

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы фигуры занимают частное положение.

Переход от общего положения геометрической фигуры к частному выполняется следующим способом: введением дополнительных плоскостей проекций, расположенных либо параллельно, либо перпендикулярно рассматриваемому геометрическому элементу.

Сущность способа заключается в том, что пространственное положение объекта не изменяют, а вводят новую, дополнительную плоскость проекций, расположенную таким образом, чтобы интересующие нас элементы фигуры или весь объект целиком проецировался на неё в удобном для решения задачи положении. При этом новая плоскость проекций должна быть перпендикулярна к одной из имеющихся плоскостей проекций. В результате образуется новая система взаимно перпендикулярных плоскостей проекций, заменяющая прежнюю.

На рис. 54 в систему плоскостей проекций введем новую плоскость проекций . Новой осью проекций будет . Заметим, что координаты Z точек А и В в плоскостях и будет одна и та же. И кроме того, если новую ось выберем параллельно проекции прямой , то на плоскости проекций проекция проектируется в натуральную величину прямой АВ.

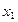
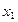
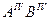
ПЕРЕВОД ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПОЛОЖЕНИЕ ПРЯМОЙ УРОВНЯ

(т.е. параллельно новой плоскости проекций )

Для преобразования прямой АВ в прямую уровня (рис. 55) вводят новую плоскость проекций так, чтобы ось проекций была параллельна проекции (рис. 54), затем откладывают на новой плоскости проекций от оси ( ) координаты Z точек и , равные координатам Z точек и .

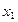
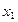
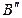
Новая проекция прямой дает натуральную величину отрезка АВ и угол наклона прямой к плоскости проекций .

ПЕРЕВОД ПРЯМОЙ УРОВНЯ В ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ

(т.е. перпендикулярно плоскости проекций)

Чтобы на новой плоскости проекций изображение прямой уровня преобразовалось в точку (рис. 56), надо эту плоскость расположить перпендикулярно данной прямой, т.е. провести на комплексном чертеже ось проекций перпендикулярно направлению проекции прямой на общую плоскость проекций. Горизонталь будет иметь своей проекцией точку на плоскости .

Для построения вырожденной в точку проекции прямой общего положения необходимо последовательно решить две предыдущие задачи: на рис. 57 представлено такое решение.

ПЕРЕВОД ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩЕЕ

Известно, что если одна плоскость перпендикулярна другой, то она должна содержать прямую, перпендикулярную этой плоскости. В качестве такой прямой можно взять прямую уровня, например, горизонталь, как это показано на рис. 58.

Переведем горизонталь h в проецирующее положение, вводя новую плоскость проекций . Поскольку проекция плоскости АВС на плоскости вырождена ыв прямую, она будет служить геометрическим местом всех точек, принадлежащих этой плоскости. Проецируем точки плоскости на , беря их координаты Z с плоскости .

ПЕРЕВОД ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТИ В ПОЛОЖЕНИЕ ПЛОСКОСТИ УРОВНЯ

Решение этой задачи позволяет определить натуральную величину плоской фигуры (рис. 59.).

Пусть задана фронтально-проецирующая плоскость . Вводим новую плоскость проекций , параллельную . Новая ось проекций по этой причине будет расположена параллельно , т.е. в системе плоскостей проекций плоскость займет положение плоскости уровня, а треугольник АВС будет проецироваться на плоскость в натуральную величину.

Если в исходном положении плоскость занимает общее положение, а нужно получить её изображение как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно две предыдущие задачи. При первой замене плоскость становится проецирующей (вырождается в линию), а при второй – плоскостью уровня (рис. 60 – не приведён). Расстояние для построения проекций точек на плоскости нужно брать с плоскости , отмеряя их от оси проекций .

Источник