Опишите способ получения десятичного числа по его дополнительному коду

Получение числа по его дополнительному коду

а) Если в коде старший бит числа равен 0, то есть число положительное. Такое число переводим в десятичную систему счисления в соответствии с правилами позиционной системы исчисления;

б) Если в коде старший бит числа равен 1, то число отрицательное, тогда:

1) инвертируем число;

3) переводим в десятичную систему счисления в соответствии с правилами позиционной системы исчисления;

4) записываем со знаком «-».

Использование дополнительного кода позволяет заменить операцию вычитания на операцию сложения.

Пример 11

Пример 12

Провести следующие вычисления в двоичной форме: 25₁₀ – 35₁₀ = — 10₁₀

= 1101 1100₂ инверсия модуля числа — 35₁₀

1101 1101₂ дополнительный код числа — 35₁₀

+	дополнительный код числа — 3510
	старший разряд 1
инверсия результата
+	+ 1
	результат вычитания

Проверка: 0000 1010₂ = 0·2 7 + 0·2 6 + 0·2 5 + 0·2 4 + 1·2 3 + 0·2 2 + 1·2 1 + 0·2 0 = 10₁₀

Пример 13

Провести следующие вычисления в шестнадцатеричной форме: 44₁₀ – 59₁₀ = — 15₁₀

= С4₁₆ инверсия модуля числа — 59₁₀

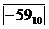
С5₁₆ дополнительный код числа — 59₁₀

С
+	С	дополнительный код числа — 3510
	F	старший разряд 1
Е	инверсия результата
+	+ 1
	F	результат вычитания

Проверка: 0F₁₆ = 0·16 1 + 15·16 0 = 15₁₀

Представление вещественных чисел

Для практических вычислений формат с плавающей запятой не используется – это формат представления чисел в памяти ЭВМ, не удобна.

Вещественное число N можно представить в системе счисления с основанием k в виде полинома:

,

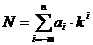
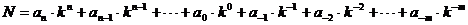
здесь дробная часть любого вещественного числа содержит ∞ число членов.

Перевод вещественных положительных чисел из 10-ной системы счисления в систему с основанием Р

1) целая часть переводится как в случае с целыми числами;

2) дробная часть умножается на Р, целая часть результата запоминается и отбрасывается.

3) вновь полученная дробная часть умножается на Р и т.д.

4) Процедура продолжается до тех пор, пока дробная часть не станет равной нулю (или в пределе стремится к нулю, т.к. дробь в пределе является бесконечной);

5) полученный код отделяем от целой части запятой.

Пример 14

Перевести число 10,1₁₀ в двоичный вид

1. целая часть числа 10₁₀ = 1010₂

2. дробная часть числа 0,1

N п/п	запоминаем
0,1	×	0,2
0,2	×	0,41
0,4	×	0,8
0,8	×	1,6
0,6	×	1,2
0,2	×	0,4
0,4	×	0,8
0,8	×	1,6
0,6	×	1,2
0,2	×	0,4

Проверка: 10,0001100110₂ = 1·2 3 + 0·2 2 + 1·2 1 + 0·2 0 + 0·2 -1 + 0·2 -2 + 0·2 -3 + 1·2 -4 + 1·2 -5 +

0·2 -6 + 0·2 -7 + 1·2 -8 + 1·2 -9 + 0·2 -10 = 10,099609…

Видно, что результат и исходное число в дробной части отличаются.

Вычислим погрешность для дробной части нашего случая с числом двоичных разрядов после запятой 10

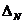
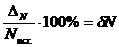
N_{исходное} – N_{получившееся} = абсолютная погрешность

относительная погрешность в процентах.

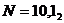
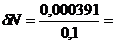
В нашем случае для : 0,391%.

Расчеты целесообразно вести до разумных пределов по погрешности или до ограничения разрядной сеткой.

Пример 15

Переведем число 973,232₁₀ в шестнадцатеричный код

N п/п	запоминаем
0,232	×	3,712
0,712	×	11,392	В
0,392	×	6,272
0,272	×	4,352

Ограничим число разрядов после запятой. Перевести число 3CD,3B₁₆ в десятичный код:

3CD,3B₁₆ = 3·16 2 + 12·16 1 + 13·16 0 + 3·16 -1 + 11·16 -2 = 973,23047₁₀

Погрешность 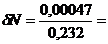0,202 %

Сложение дробной части вещественного числа в любой системе исчисления осуществляется традиционным образом, т.е. как и децимальной. При этом перенос в целую часть числа особенностей не имеет.

Пример 16

Сложить числа 0,5₁₀ + 0,625₁₀ = 1,125₁₀ в двоичной форме

0,
+	0,
	1,

Проверка: 1,001₂ = 1·2 0 + 0·2 -1 + 0·2 -2 + 1·2 -3 = 1,125₁₀

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Дополнительный код (представление числа)

Дополнительный код (англ. two’s complement , иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.

Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]

Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2).

Содержание

Представление отрицательного числа в дополнительном коде

При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно , что равно 127.

Десятичное представление	Код двоичного представления (8 бит)
	прямой	обратный	дополнительный
127	01111111	01111111	01111111
1	00000001	00000001	00000001
0	00000000	00000000	00000000
-0	10000000	11111111	—
-1	10000001	11111110	11111111
-2	10000010	11111101	11111110
-3	10000011	11111100	11111101
-4	10000100	11111011	11111100
-5	10000101	11111010	11111011
-6	10000110	11111001	11111010
-7	10000111	11111000	11111001
-8	10001000	11110111	11111000
-9	10001001	11110110	11110111
-10	10001010	11110101	11110110
-11	10001011	11110100	11110101
-127	11111111	10000000	10000001
-128	—	—	10000000

Дополнительный код для десятичных чисел

Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).

При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):

10-ричная система счисления («обычная» запись)	10-ричная система счисления, дополнительный код
.	.
13	0013
12	0012
11	0011
10	0010
9	0009
8	0008
.	.
2	0002
1	0001
0	0000
-1	9999
-2	9998
-3	9997
-4	9996
.	.
-9	9991
-10	9990
-11	9989
-12	9988
.	.

Преобразование в дополнительный код

Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.

1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1

Допишем слева знаковый единичный разряд

Для обратного преобразования используется тот же алгоритм. А именно:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1 и проверим, сложив с дополнительным кодом

p-адические числа

В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000. (1) равно 4444. (−1).

Источник

Дополнительный код (представление числа)

Материал из Seo Wiki — Поисковая Оптимизация и Программирование

Дополнительный код (англ. two’s complement , иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение). Либо вычитанием числа из нуля.

Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]

Дополнение до 2 двоичного числа определяется как величина полученная вычитанием числа из наибольшей степени двух (из 2 N для N-битного дополнения до 2). [2]

Содержание

Представление числа в дополнительном коде

При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом. Если же знаковый разряд равен 1, то в остальных разрядах записано отрицательное двоичное число, преобразованное в дополнительный код. Для получения значения, которое противоположно по знаку, все разряды, включая знаковый, инвертируются, а затем к результату добавляется единица.

Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно 2^7-1 , что равно 127.

Десятичное представление	Код двоичного представления (8 бит)
	прямой	дополнительный
127	01111111	01111111
1	00000001	00000001
0	00000000	00000000
-0	10000000	———
-1	10000001	11111111
-2	10000010	11111110
-3	10000011	11111101
-4	10000100	11111100
-5	10000101	11111011
-6	10000110	11111010
-7	10000111	11111001
-8	10001000	11111000
-9	10001001	11110111
-10	10001010	11110110
-11	10001011	11110101
-127	11111111	10000001
-128	———	10000000

При применении той же идеи к привычной 10-ричной системе счисления получится (например, для гипотетического процессора использующего 10-ричную систему счисления):

10-ричная система счисления («обычная» запись)	10-ричная система счисления, дополнительный код
.	.
13	0013
12	0012
11	0011
10	0010
9	0009
8	0008
.	.
2	0002
1	0001
0	0000
-1	9999
-2	9998
-3	9997
-4	9996
.	.
-9	9991
-10	9990
-11	9989
-12	9988
.	.

Преобразование дополнительного кода

Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.

1. Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
2. Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1

Допишем слева знаковый единичный разряд

Для обратного преобразования используется тот же алгоритм. А именно:

Инвертируем все разряды числа, получая таким образом обратный код:

Добавим к результату 1 и проверим, сложив с дополнительным кодом

Дополнительный код для десятичных чисел

Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).

Источник