Описать способ ввода числовых последовательностей

Числовая последовательность

Последовательность чисел, имеющую определенный интервал, можно ввести двумя способами:

1) Первый способ заключается в том, что в две начальные ячейки последовательности вводятся первые два числа через нужный интервал. Затем обе ячейки нужно выделить. При этом, как говорилось выше, в нижнем правом углу выделения появляется маркер распространения. При приближении к нему курсора мыши он превращается в маленький крестик. Если отбуксировать маркер распространения на весь необходимый диапазон ячеек, диапазон заполнится нужной последовательностью чисел.

2) Второй способ ввода числовой последовательности нужно начинать с занесения в первую ячейку числа начала последовательности. Затем выделить весь диапазон ввода и выполнить команду ПРАВКА Þ ЗАПОЛНИТЬ Þ ПРОГРЕССИЯ. Появляется диалоговое окно «Прогрессия» (рис. 34), в котором нужно выбрать тип прогрессии, шаг и предельное значение последовательности и нажать ОК. Выделенный диапазон ячеек заполнится прогрессией чисел в соответствии с установками в диалоговом окне.

Последовательность слов

Достаточно часто требуется вводить определенную последовательность слов, например, названия месяцев, дней недели и т.д. Эта возможность предусмотрена в Excel. Достаточно ввести в одну ячейку название любого дня недели или месяца полностью или коротко, завершить ввод и отбуксировать маркер распространения этой ячейки в любую сторону. Диапазон заполнится последовательностью названий.

Предусмотрена возможность задания аналогичной собственной последовательности. Для этого нужно выполнить команду СЕРВИС Þ ПАРАМЕТРЫ. В открывшемся диалоговом окне «Параметры» перейти на вкладку «Списки». В окне «Списки» (рис. 35) показаны списки последовательностей, уже имеющихся в программе. Для создания другого списка нужно щелкнуть кнопку диалогового окна «Добавить» и в поле «Элементы списка» ввести свой список. При этом после ввода каждого элемента списка требуется нажимать Enter. После окончания ввода списка щелкнуть ОК.

Дата добавления: 2014-12-24 ; просмотров: 1747 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Ввод последовательностей в MS Excel

Excel позволяет вводить последовательности чисел, дать, дней недели и месяцев автоматически. Выясним, в чем заключается функция автозаполнения ячеек. Для этого рассмотрим несколько видов последовательностей.

Числовые последовательности

Чтобы, к примеру, сделать нумерацию строк, можно вводить номера 1, 2, 3 и т.д. вручную. А можно использовать автозаполнение.

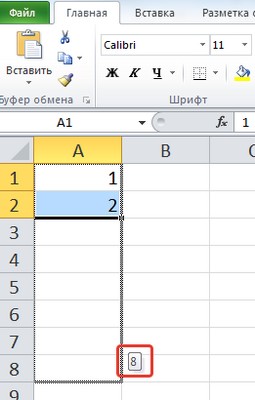
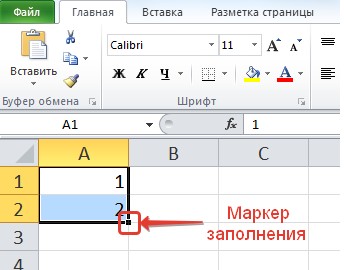
Для автоматического ввода номеров напишем в ячейке А1 число 1, в ячейке А2 число 2. Выделим обе ячейки. Обратим внимание, что при наведении курсора в правый нижний угол ячейки А2 появился черный квадратик — это маркер заполнения.

Если навести на него курсор мыши, то курсор примет вид черного крестика. Теперь нужно нажать левую кнопку мыши и, удерживая, потянуть вниз. Рядом с курсором появляется значение, которое будет введено в последнюю ячейку, если отпустить кнопку мыши.

• Если в ячейку А1 ввести значение 1, а потом нажать на клавиатуре клавишу Ctrl и потянуть вниз за маркер заполнения этой ячейки, то значения следующих ячеек будут увеличиваться на 1.
• Чтобы ввести последовательность нечетных чисел (шаг увеличения чисел равен 2), введем в ячейку А1 число 1, а в ячейку А2 число 3. Далее выделим обе ячейки и за маркер заполнения потянем вниз. Мы получим последовательность чисел 1, 3, 5, 7 и т.д.
• Аналогично можно получить последовательность четных чисел, для этого нужно ввести числа 2 и 4 (шаг равен 2).
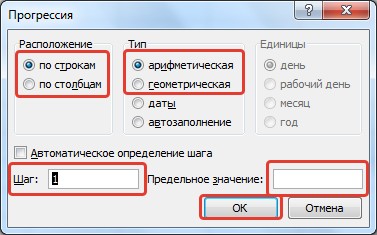
• Ввод арифметической (геометрической) прогрессии. Для создания арифметической прогрессии введем в ячейку А1 значение первого члена прогрессии. На вкладке Главная в группе Редактирование выберем команду Заполнить — Прогрессия.

В диалоговом окне Прогрессия можно установить параметры: Расположение, Тип прогрессии, Шаг, Предельное значение.

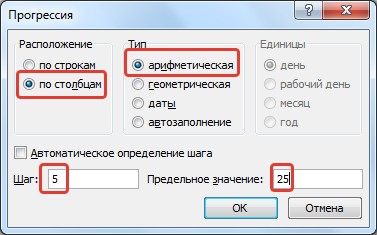
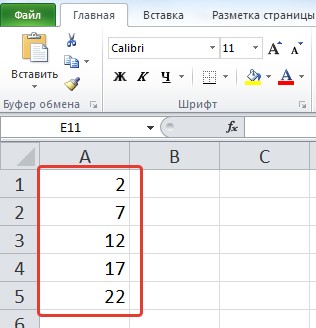
Если выбрать расположение по столбцам арифметической прогрессии с шагом 5 и предельным значением 25 (при этом в ячейке А1 введено значение 2, а сама ячейка выделена), то получим следующее заполнение:

Примечание

• Автозаполнение можно использовать не только по столбцам, но и по строкам. Для этого нужно вводить начальные значения в сроке и перетаскивать маркер заполнения не вниз, а вправо.
• Если нужно заполнять последовательность чисел в порядке возрастания, то маркер нужно перетаскивать вниз или вправо. Если в порядке убывания — вверх или влево.

Последовательность дней недели

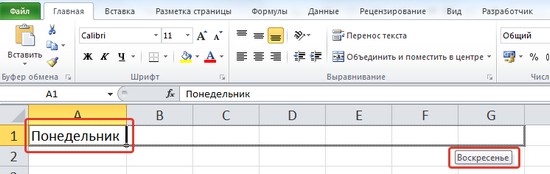
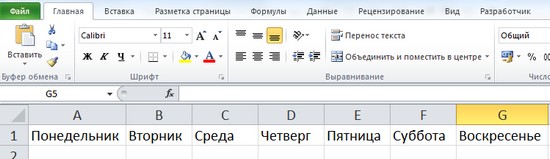
Чтобы ввести последовательность дней недели, достаточно в первую ячейку ввести Понедельник (или другой день) и потянуть за маркер заполнения этой ячейки в нужном направлении.

Последовательность Месяцы

Точно так же, как и в примере последовательности дней недели, в Excel можно получить последовательность месяцев, введя в первую ячейку нужный месяц (например, январь).

Последовательность дат

Введя в ячейку дату (например, 20.06.2015), можно получить последовательность дат.

Повторение последовательности

Если в ячейки А1, А2, А3 введены числа 1, 2, 3 соответственно и мы хотим, чтобы эта последовательность повторялась, выделим эти ячейки и при нажатой клавише Ctrl за маркер заполнения протянем вниз (или вправо), то мы получим последовательность 1, 2, 3, 1, 2, 3, 1, 2, 3…

Примечание

При использовании функции автозаполнения рядом с диапазоном появляется кнопка Параметры автозаполнения. При нажатии на нее можно выбрать нужный вариант.

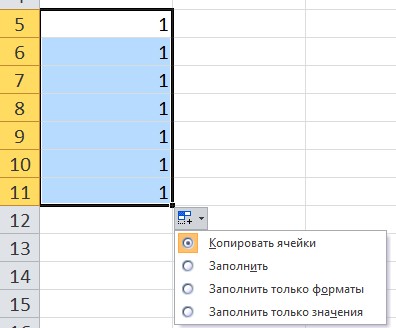
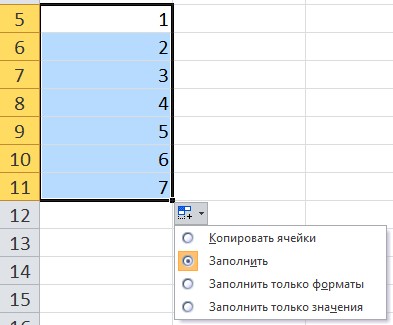
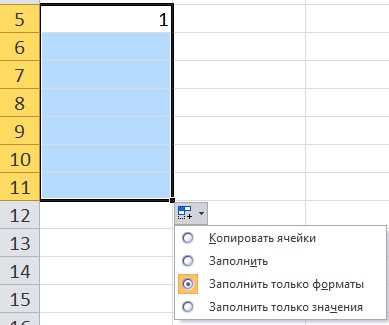
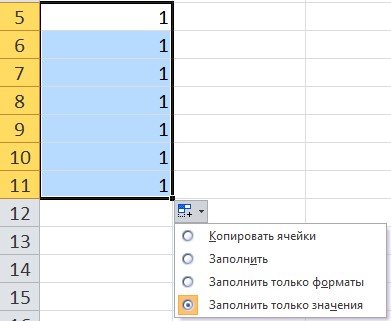
В качестве примера введем в ячейку значение 1, за маркер заполнения протянем вниз. Обратим внимание, какой результат будет, если выбрать каждый из вариантов автозаполнения:

• Копирование ячейки — все значения равны 1.
• Заполнить — получим прогрессию с шагом 1.
• Заполнить только форматы — не будет значений, копируется форматирование ячеек.

Заполнить только значения — все значения равны 1, при этом форматирование ячейки не копируется.

Кстати, Excel позволяет делать свои списки последовательностей, которые потом можно использовать для автозаполнения таблиц. Читайте инструкцию >>>

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Источник

Числовые последовательности. Способы их задания.

Урок № 32 АЛГЕБРА

Учитель математики, первой категории Гаун Ольга Викторовна. Восточно-Казахстанская область Глубоковский район КГУ «Черемшанская средняя школа»

Тема: Числовая последовательность и способы ее задания

Основные цели и задачи урока

Образовательная: разъяснить учащимся смысл понятий «последовательность», «n-ый член последовательности»; познакомить со способами задания последовательности.

Развивающа я: развитие навыков логического мышления; развитие вычислительных навыков; развитие культуры устной речи, развитие коммуникативности и сотрудничества. Воспитательная : воспитание наблюдательности, привитие любви и интереса к предмету.

Ожидаемые результаты освоения темы

В ходе урока приобретут новые знания о числовых последовательностях и способах ее задания. Научатся находить верное решение, составлять алгоритм решения и пользоваться им при решении заданий. Путем исследования обнаружат их некоторые свойства. Вся работа сопровождается слайдами. Применение ИКТ даст возможность провести урок оживленно, выполнить большой объем работы, со стороны ребят будет искренний интерес и эмоциональное восприятие. Одарённые ученики выступят с сообщением о числах Фибоначчи и о золотом сечении. Универсальные учебные действия, на формирование которых направлен образовательный процесс: умение работать в паре, развивать логическое мышление, умение анализировать, исследовать, делать выводы, отстаивать свою точку зрения. Обучить навыкам общения и сотрудничества. Использование данных технологий способствует развитию у обучающихся универсальных способов деятельности, опыта творческой деятельности, компетентности, коммуникабельности.

Ключевые идеи урока

Новые подходы в преподавании и обучении

— обучение тому, как обучаться

Обучение критическому мышлению

Обучение талантливых и одарённых детей

Изучение новой темы

Наглядный (презентация), словесный (беседа, объяснение, диалог), практический.

Формы организации учебной деятельности уч-ся

фронтальная; парная; индивидуальная.

(Приветствие учащихся, определение отсутствующих, проверка готовности учащихся к уроку, организация внимания).

«Числа управляют миром»,- говорили древнегреческие ученые. «Все есть число». Согласно их философскому мировоззрению, числа управляют не только мерой и весом, но также явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире. Сегодня на уроке мы продолжим работать с числами.

Введение в тему, изучение нового материала.

Давайте проверим ваши логические способности. Я называю несколько слов, а вы должны продолжить:

– январь, февраль, март…;

– Алиев, Гордеева, Грибачева… (список класса);

Вывод: Это последовательности, то есть некоторый упорядоченный ряд чисел или понятий, когда каждое число или понятие стоит строго на своем месте. Итак, тема урока – последовательность.

Сегодня мы будем говорить о видах и составляющих числовых последовательностей, а также о способах их задания. Последовательности будем обозначать так: (аn), (bn), (сn) и т.д.

А сейчас я предлагаю вам первое задание: перед вами некоторые числовые последовательности и словестное описание этих последовательностей. Вам необходимо найти закономерность каждого ряда и соотнести с описанием. (показать с помощью стрелки) (Взаимопроверка)

Рассмотренные нами ряды и есть примеры числовых последовательностей .

Элементы, образующие последовательность, называются членами последовательности и называются соответственно первым, вторым, третьим,… n — ным членами последовательности. Обозначают члены последовательности так а ₁ ; а ₂ ; а ₃ ; а ₄ ; … а _n ; где n – номер , под которым данное число находится в последовательности.

На экране записаны последовательности:
( На перечисленных последовательностях отрабатываются форма записи члена последовательности a _n , и понятия предыдущего и последующего членов ) .
3; 6; 9; 12; 15; 18;…
5, 3, 1, -1.
1, 4, 9, 16 ,…
–1; 2; –3; 4; –5; 6; …
3; 3; 3; 3; …; 3; … .

Назовите а ₁ для каждой последовательности, а ₃ и т.д. А смогли бы вы продолжить каждый из этих рядов? Что для этого необходимо знать?

Давайте разберем с вами еще такие понятия как последующий и предыдущий .

Виды последовательностей
( на перечисленных выше последовательностях отрабатывается навык определять виды последовательностей )
1) Возрастающая – если каждый член меньше следующего за ним, т.е. a _n a _{n +1.}
2) Убывающая – если каждый член больше следующего за ним, т.е. a _n > a _{n +1} .
3) Бесконечная
4) Конечная
5) Знакочередующаяся
6) Постоянная (стационарная)

Попробуйте дать определение каждому виду и охарактеризуйте каждую из предложенных последовательностей.

Задания для устной работы

Назовите в последовательности 1; 1/2; 1/3; 1/4; 1/5; … 1/n; 1/(n+1) члены а ₁ ; а ₄ ; а ₁₀ ; а _n ;

Является ли последовательность четырёхзначных чисел конечной? (да)

Назовите её первый и последний члены. (Ответ: 1000; 9999)

Является ли последовательностью запись чисел 2; 4; 7; 1; -21; -15; …? (нет, так как нельзя по первым шести членам обнаружить какую-нибудь закономерность)

Физпауза (тоже связана с темой сегодняшнего урока: звездное небо, планеты солнечной системы…в чем связь?)

Способы задания последовательностей
1) словесный – задание последовательности описанием;
2) аналитический – формулой n -го члена;
3) графический – с помощью графика;
4) рекуррентный – любой член последовательности, начиная с некоторого, выражается через предыдущие
Сегодня на уроке мы разберем первых два способа. Итак, словестный способ. Может быть кто-нибудь из вас попробует задать какую-либо последовательность?

( Например: Составьте последовательность нечетных натуральных чисел . Охарактеризуйте эту последовательность: возрастающая, бесконечная)
Аналитический способ: с помощью формулы n-ого члена последовательности.

Формула общего члена позволяет вычислить член последовательности с любым заданным номером. Например, если х _n =3n+2, то

х ₄₅ =3 . 45+2=137 и т.д. Так каково преимущество аналитического способа перед словестным ?

А я вам предлагаю следующее задание: даны формулы задания некоторых последовательностей и сами последовательности, образованных по этим формулам. В этих последовательностях пропущены некоторые члены. Ваша задача, работая в парах , заполнить пропуски.

Самопроверка (на слайде появляется правильный ответ)

Представление творческого проекта «Числа Фибоначчи» ( опережающее задание )

Сегодня мы познакомимся со знаменитой последовательностью:

1, 1, 2, 3, 5, 8, 13, 21, …, (Слайд) Каждое число, начиная с третьего, равно сумме двух предшествующих. Этому ряду натуральных чисел, имеющему своё историческое название – ряд Фибоначчи, присуща своя логика и красота. Леонардо Фибоначчи (1180-1240). Крупный итальянский математик, автор «Книги абака». Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!).

Наверное, вы не совсем поняли какова связь между спиралью и рядом Фибоначчи. Поэтому я покажу, как она получается .

Если мы построим рядом два квадрата со стороной 1,затем набольшей стороне равной 2 другой, затем на большей стороне, равной 3 еще квадрат так до бесконечности…Потом в каждом квадрате, начиная с меньшего, построим четверть дуги, то получим спираль, о которой идет речь в фильме.

На самом деле практическое применение знаний, полученных на этом уроке в реальной жизни достаточно велико. Перед вами несколько задач из разных научных областей.

Задача 1. Продолжи последовательности чисел:

16, 15, 18, … (17, 20, 19)

1, 2, 2, 4, 8, … (32, 256, 8192)

33, 31, 32, … (30, 31, 29)

Задача 2. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день?

(Ответы учащихся записываются на доске: 500, 530, 560, 590, 620).

Задача 3. Автомобиль, двигаясь со скоростью 1 м/с за каждую последующую секунду изменял свою скорость на 0,6 м/с. Какую скорость он будет иметь спустя 10 секунд?

Задача 4. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Через сколько дней заболеют все ученики нашей школы (300 человек)? (Через 4 дня).

Задача 5 . Сколько появится бактерий куриной холеры за 10 часов, если одна бактерия делится пополам каждый час?
Задача 6 . Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин? ( 10)

Задача 7 . При свободном падении тело проходит в первую секунду 4,8 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.

Задача 8 . Гражданина К. осталось завещание. Он в первый месяц истратил 1000$, а каждый последующий месяц истратил на 500$ больше. Сколько денег было завещано гражданину К., если их хватит на 1 год безбедной жизни? (45000)

Быстро и без ошибок решать такие задачи нам позволит изучение следующих тем этой главы «Прогрессии».

Домашнее задание: стр.66 №151, 156, 157

Творческое задание: сообщение о треугольнике Паскаля

Подведение итого. Рефлексия. (оценка «приращения» знаний и достижения целей)

Источник