Графический способ записи алгоритма.
Дата добавления: 2015-06-12 ; просмотров: 2097 ; Нарушение авторских прав
Наиболее наглядным и понятным способом представления алгоритма является его описание в виде блок-схем. Алгоритм при этом изображается в виде определённой последовательности блоков, предназначенных для выполнения отдельных функций, и связей между блоками. Внутри блоков содержится информация, поясняющая выполняемые ими действия. Часто каждый блок снабжают номером, который размещается в левой верхней его части.
В таблице 1 приведены некоторые наиболее часто используемые блоки и пояснения выполняемых ими функций. Размер а должен выбираться из ряда 10,15,20, . мм, размер b равен 1.5а. В схемах алгоритма обычно увеличивают ширину блоков (размер b) для удобства записи информации.
На схеме алгоритма ход вычислительного процесса отражается обязательно стрелками. Направление линий связи сверху вниз и слева направо принимают за основное; если линии связи основного направления не имеют изломов, то их направление стрелками можно не обозначать. В остальных случаях направление линий связи обозначать стрелкой обязательно.
Блок-схема —это способ описания алгоритмов, где действия представлены в виде блоков, а последовательность в виде стрелок между ними.
Таблица 1.1
| Название блока | Обозначение | Выполняемая функция | |||
| Начало и конец |  | Вход и выход в отдельно описанных алгоритмах и подпрограммах. | |||
| Ввод и вывод |  | Задание численных значений исходных данных и фиксация результатов расчета. Имеет один выход. | |||
| Вычислительный блок |  | Запись расчетных формул: слева от знака равенства записывается вычисляемая переменная, справа — расчетная формула. | |||
| Блок условия (логический блок) |  | Проверка условия и выбор направления хода вычислительного процесса. Имеет два выхода: “да”(знак “+”) при выполнении условия, “нет”(знак “-”) — в противном случае. | |||
| модификация |
| Начало цикла | |||
| Соединитель |  | Указание связи между прерванными линиями потока. | |||
| Предопределенный процесс |  | Использование ранее созданных и отдельно описанных алгоритмов или программ |
Алгоритм, записанный в виде блок- схемы, не требует дополнительных объяснений, позволяет даже мало сведущему в информатике человеку очень наглядно представить и проследить последовательность действий, необходимых для решения задачи. Поэтому изображение алгоритмов в виде блок- схем используется в настоящее время наиболее широко. Часто в блоке условия вместо “да” используют “+”, а вместо “нет” используют “-”.
Пример.Дано число х. Рассчитать Y, где Y= 
Рис. 1.1
1.3 ОСНОВНЫЕ СТРУКТУРЫ АЛГОРИТМОВ
Основные структуры алгоритмов —это ограниченный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий.
К основным структурам алгоритмов относятся:
§ следование;
§ ветвление;
§ повторение.
1.3.1 Алгоритмы линейной структуры
Алгоритм линейной структуры (следование) —алгоритм, в котором все действия выполняются последовательно друг за другом.
Пример.Составить алгоритм вычисления объёма прямоугольного параллелепипеда. Диагональ параллелепипеда, равная d см, составляет с плоскостью основания угол a˚, а с боковой гранью угол b˚. Одна из сторон основания равна а см.
 |
Рис. 1.2
Для вычисления объёма прямоугольного параллелепипеда необходима следующая формула: V=abc.
Из формулы видно, что для нахождения объёма необходимо сначала найти длину b и высоту c параллелепипеда. Из соотношения углов и сторон прямоугольного треугольника (рис.2) можно выразить искомые стороны: b = d×Sinb иc = d×Sina.
Представим решение задачи в виде блок-схемы:
Рис. 1.3 | Так как линейный алгоритм представляет собой набор команд, выполняемых последовательно друг за другом, то все блоки алгоритма будут располагаться друг под другом в определенной последовательности, согласно условию задачи. Только вычислив b и c, возможно определить V. Все блоки алгоритма, кроме блоков ввода и вывода будут вычислительными. В блоке ввода записывается слово “Ввод” и перечисляются исходные данные (переменные a, a, b). В блоке вывода записывается слово “Вывод” и перечисляются переменные, которые являются результатом расчета. В нашем примере выводится одна переменная V. | |
| Пример.Составить алгоритм вычисления значения выражения для исходных данных x и y. | ||
 рис. 1.4 | На практике линейные алгоритмы используются в основном при расчете громоздких формул. |
1.3.2 Алгоритмы разветвляющейся структуры
На практике редко удается представить схему алгоритма решения задачи в виде линейной структуры. Часто в зависимости от каких-либо значений промежуточных результатов необходимо организовать вычисление либо по одним, либо по другим формулам.
Разветвляющийся алгоритм содержит блок (или блоки) проверки некоторого условия. В зависимости от выполнения условия вычислительный процесс может идти по одному или другому направлению. Каждое из возможных направлений вычисления называется ветвью. В качестве вычислительного процесса может выступать одно действие или последовательность действий.
Алгоритм разветвляющейся структуры (ветвление)– алгоритм, в котором предусмотрено разветвление указанной последовательности действий на несколько направлений в зависимости от итога проверки условия.
На рисунках 5а, 5b, 5c продемонстрированы в условных обозначениях схемы основных конструкций разветвляющихся алгоритмов:
— ответвление;
— раздвоение;
— выбор.
В конструкции Ответвление происходит выполнение вычислительного процесса только по одному из направлений. На приведенной в рис.5а схеме — по направлению, указанному знаком «+»:
 |
Рис. 1.5а.Конструкция –Ответвление
В конструкции Раздвоениев зависимости от итога проверки условия происходит выполнение либо одного вычислительного процесса, либо другого: если условие выполняется, то процесс продолжается по направлению, указанному знаком «+», иначе (условие не выполняется) – по направлению, указанному знаком «-».
Рис. 1.5b.Конструкция — Раздвоение
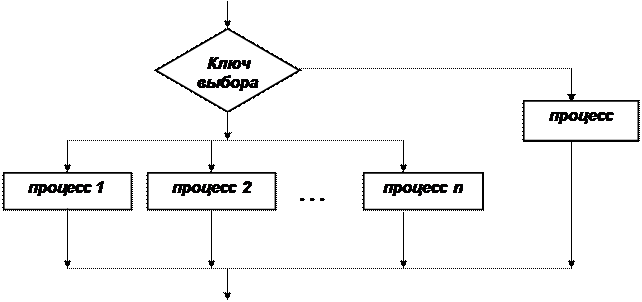
В конструкции Выборв зависимости от значения ключа выбора происходит выбор одного из нескольких возможных направлений и выполнение соответствующего ему вычислительного процесса.
Рис. 1.5с. Конструкция – Выбор
Рассмотрим примеры на каждую из конструкций разветвляющейся структуры.
Пример.Составить алгоритм изменения значений двух заданных чисел: удвоить те из них, которые принадлежат интервалу [1;5].
Рис. 1.6 | На данной блок-схеме продемонстрированы две последовательно расположенные друг за другом конструкции — Ответвление. Рассматриваемый алгоритм имеет две ветви: в одной, если переменная принадлежит заданному интервалу (условие выполняется), то ее значение удваивается, а в другой (условие не выполняется) – никаких действий над переменной не предполагается. | |
Пример.Дано число х. Рассчитать  | ||
 Рис. 1.7 | В данном примере продемонстрирована конструкция Раздвоение. В зависимости от введенного значения аргумента Х переменная Y принимает одно из двух возможных значений: Sinx или Cosx. |
Пример.Составить алгоритм нахождения корней квадратного уравнения ax 2 +bx+c=0 в зависимости от коэффициентов а, b и с.
 Рис. 1.8 | Алгоритм решения данного примера можно записать в виде линейной структуры. Однако, для удовлетворения свойств массовости и результативности алгоритма необходимо, чтобы при любых исходных данных был получен результат или сообщение о том, что задача не может быть решена при заданных исходных данных. Действительно, если D 0. После его проверки происходит вычисление значения Y по одной из двух оставшихся формул. |
 Пример.Дано число х. Рассчитать  | |
| Рис. 1.10 |
В данном примере продемонстрирована конструкция Выбор, где ключом выбора является переменная n. В зависимости от введенного значения этой переменной, равного 0, 1, 2 или 3, происходит выбор формулы для вычисления Z. При всех других значениях n, (отличных от 0, 1, 2, 3) Z вычисляется по формуле x 2 .
1.3.3 Алгоритмы циклической структуры
Существует множество задач, в которых многократно используются одни и те же команды для различных данных. Обойтись только линейными и разветвляющими алгоритмами в этих случаях не всегда удаётся. Для данных ситуаций существуют циклические алгоритмы.
Алгоритмы циклической структуры (повторение) – алгоритмы, отдельные действия в которых многократно повторяются.
С алгоритмом циклической структуры тесно связаны следующие понятия:
Цикл – выполнение определенного набора команд некоторое количество раз.
Тело цикла – многократно повторяющиеся действия алгоритма.
Параметр цикла – величина, с изменением которой связано многократное выполнение цикла.
· с заранее известным числом повторений – условием окончания повторения является достижение параметра цикла своего конечного значения;
· с заранее неизвестным числом повторений – условие повторения или окончания цикла задается по некоторому вычисляемому промежуточному или окончательному результату, например, пока не будет достигнута требуемая точность вычисления.
Источник
Алгоритмы
Алгоритмы. Разработка алгоритма решения задачи
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.
Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x y, то переход к шагу 6, иначе к шагу 7.
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.
Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
Источник
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|