Одинаковым способом для каждой буквы

13. Перестановки с повторениями

При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.

Общую задачу сформулируем следующим образом.

Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?

Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

, (11.1) где .

Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

.

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

.

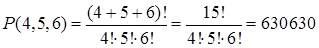
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

.

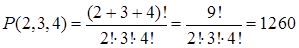
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

.

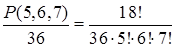
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

.

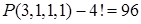
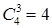
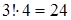
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .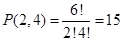

11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .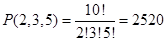

11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .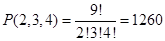

11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .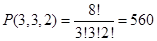

11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .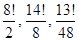

11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .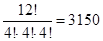

11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .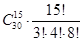

11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .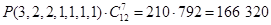

11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

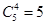
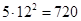
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

Источник

Дана кодовая таблица флажковой азбуки. Разгадайте зашифрованную фразу

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Дана кодовая таблица флажковой азбуки. Разгадайте зашифрованную фразу.

Дана кодовая таблица флажковой азбуки. Разгадайте зашифрованную фразу.

Дана кодовая таблица флажковой азбуки. Разгадайте зашифрованную фразу.

Дана кодовая таблица флажковой азбуки. Разгадайте зашифрованную фразу.

По таблице восстанови рисунок в сетке.

2 – зеленый цвет

3 – коричневый цвет

По таблице восстанови рисунок в сетке.

2 – красный цвет

По таблице восстанови рисунок в сетке.

3 – голубой цвет

По таблице восстанови рисунок в сетке.

2 – зеленый цвет

Анаграммы – это головоломки, в которых переставляются буквы в словах. Расшифруйте слова в анаграммах. Выберите лишнее слово (объясните).

Анаграммы – это головоломки, в которых переставляются буквы в словах. Расшифруйте слова в анаграммах. Выберите лишнее слово (объясните).

Анаграммы – это головоломки, в которых переставляются буквы в словах. Расшифруйте слова в анаграммах. Выберите лишнее слово (объясните).

Анаграммы – это головоломки, в которых переставляются буквы в словах. Расшифруйте слова в анаграммах. Выберите лишнее слово (объясните).

Неожиданно осветилась стена над камином, и Золушка увидела следующую надпись: НБМЁОЭЛЙК ГПМЩЁВОЙЛ . Помоги ей прочитать сообщение, если известно, что для его составления использовались 33 буквы, а само сообщение было искажено при прохождении через волшебный канал передачи информации одинаковым способом для каждой буквы.

Н Б М Ё О Э Л Й К

Г П М Щ Ё В О Й Л

Неожиданно осветилась стена над камином, и Золушка увидела следующую надпись: ЦСФТУБМЭОБА ЛБСЁУБ . Помоги ей прочитать сообщение, если известно, что для его составления использовались 33 буквы, а само сообщение было искажено при прохождении через волшебный канал передачи информации одинаковым способом для каждой буквы.

Ц С Ф Т У Б М Э О Б А

Неожиданно осветилась стена над камином, и Золушка увидела следующую надпись: РСЙДПУПГЭТА ИПМФЩЛБ . Помоги ей прочитать сообщение, если известно, что для его составления использовались 33 буквы, а само сообщение было искажено при прохождении через волшебный канал передачи информации одинаковым способом для каждой буквы.

Р С Й Д П У П Г Э Т А

Неожиданно осветилась стена над камином, и Золушка увидела следующую надпись: ЦСФТУБМЭОЬЁ УФХЁМЭЛЙ . Помоги ей прочитать сообщение, если известно, что для его составления использовались 33 буквы, а само сообщение было искажено при прохождении через волшебный канал передачи информации одинаковым способом для каждой буквы.

Ц С Ф Т У Б М Э О Ь Ё

У Ф Х Ё М Э Л Й

Вини-Пух, прогуливаясь через лес, зашел к Пятачку. Затем они вместе пошли к Кролику, и потом втроем отправились к озеру. Какой номер схемы отображает маршрут друзей?

Вини-Пух, прогуливаясь через лес, зашел к Пятачку. Затем они вместе пошли к озеру, а потом пошли в гости к кролику. Какой номер схемы отображает маршрут друзей?

Вини-Пух с утра пришел в гости к Кролику, затем они вдвоем зашли за Пятачком и пошли гулять к озеру. Какой номер схемы отображает маршрут друзей?

Вини-Пух, прогуливаясь через лес, пройдя мимо озера, пришел в гости к Кролику. Потом они вместе зашли за Пятачком и пошли к озеру, а потом к Вини-Пуху домой. Какой номер схемы отображает маршрут друзей?

Источник