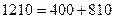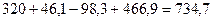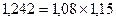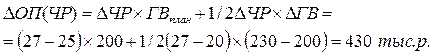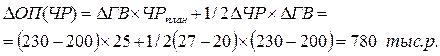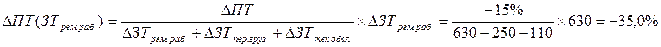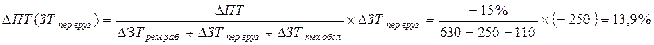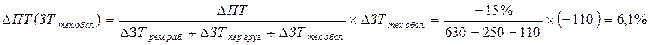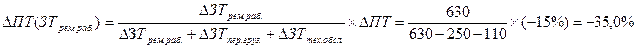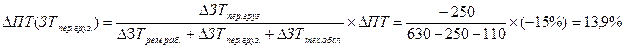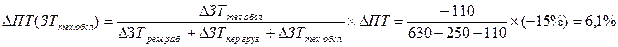Методика факторного анализа в детерминированных моделях
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину.Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1. Аддитивные модели: 
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели: 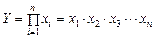
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели: 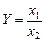
Они используются тогда, когда результативный показатель получают делением одного фактора на величину другого.
4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей:



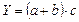
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели, как:
где ВП – валовая продукция
ЧР – среднесписочная численность работников
ГВ – среднегодовая выработка одного среднесписочного работника
ДВ – среднедневная выработка одного рабочего
Д – количество отработанных дней одним работником за год
П – продолжительность рабочего дня, ч
ЧВ – среднечасовая выработка одного рабочего
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов.
Аналогичным образом осуществляется моделирование аддитивных факторных систем, т.е. путем расчленения факторов исходной модели на составные элементы.
Как известно, объем реализации продукции равен:
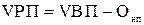
где 
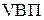
Онп – остатки нереализованной продукции.
Часть нереализованной продукции может находиться на складах предприятия (Оскл), а часть может быть отгружена покупателям, но еще не оплачена (Оотг). Тогда приведенную исходную модель можно записать следующим образом:

К классу кратных моделей применяют следующие способы их преобразования: удлинения, расширения и сокращения.
Метод удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в виде функции двух факторов: изменение суммы затрат (З) и объема выпуска продукции (VВП). Исходная модель этой факторной системы будет иметь вид:

Если общую сумму затрат (З) заменить отдельными их элементами, такими, как оплата труда (ОТ), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (НР) и др., то получим аддитивную модель с новым набором факторов:

где х1 – трудоемкость продукции;
х2 – материалоемкость продукции;
х3 – фондоемкость продукции;
х4 – уровень накладных затрат.
Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель Y = a : b ввести новый показатель c, то модель примет вид:

В результате получается конечная мультипликативная модель в виде произведения нового набора факторов.
Этот способ моделирования широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: 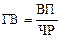

где ДВ – среднедневная выработка;
Д – количество отработанных дней одним работником.
ВП – валовая продукция
ЧР – среднесписочная численность работников
ГВ – среднегодовая выработка одного среднесписочного работника
Метод сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель. В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.
Как известно, рентабельность совокупных активов предприятия рассчитывается делением суммы прибыли (П) на их среднегодовую величину (А);
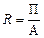
Если числитель и знаменатель разделим на выручку (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:


Процесс моделирования факторных систем – очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном анализе для этого используются следующие способы:
— логарифмирования и др.
Первые четыре способа основаны на методе элиминирования. Элиминировать — значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, затем изменяются два, затем три и т.д. при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных).
Сущность приема цепных подстановок заключается в последовательной замене базисной величины частных показателей, входящих в расчетную формулу, фактической величиной этих показателей и измерения влияния произведенной замены на изменение величины изучаемого обобщающего показателя. После каждой замены базисной величины частного показателя фактической выполняют все математические действия, предусмотренные расчетной формулой, и из полученного результата вычитают предшествующий (до замены данного показателя). Разность результатов показывает искомую величину влияния изменений данного частного показателя на обобщающий, поскольку все остальные частные показатели в сравниваемых последовательных расчетах одинаковы по величине.
Замена базисной величины частного показателя фактической называется подстановкой.
Допустим, имеется обобщающий показатель (Y), который можно представить в виде произведения частных показателей (факторов) – a, b, c.

Общее (абсолютное) отклонение обобщающего показателя:
Общее отклонение обобщающего показателя за счет изменения факторов a, b и c соответственно:
Источник
Способы детерминированного факторного анализа
Детерминированный факторный анализ — это методика изучения влияния факторов на результативный показатель, связь между которыми имеет функциональный характер. То есть результативный показатель представлен в виде произведения, алгебраической суммы или частного факторов.
Этапы проведения детерминированного факторного анализа:
· построение обоснованной детерминированной факторной модели;
· выбор приема факторного анализа;
· реализация расчетных процедур;
· формулирование выводов и рекомендаций по результатам анализа.
Построение факторной модели. В детерминированной факторной модели связи между переменными жестко фиксированы и каждой конкретной величине изменения независимой переменной (фактора) соответствует строго определенное (детерминированное) изменение зависимой переменной (результативного показателя).
На этом этапе происходит моделирование взаимосвязей между результативными показателями и факторами, которые влияют на их величину. Это очень важный этап, так как если на этом этапе будет допущена ошибка, то все дальнейшие расчеты не дадут верных результатов. Смысл этапа состоит в том, чтобы в форме математического уравнения выразить взаимосвязь исследуемого показателя и факторов.
Существует правило, которое заключается в следующем: любое расширение детерминированной факторной модели не должно противоречить логике связи «причина — следствие». То есть факторы, которые входят в модель, должны находиться в причинно-следственной связи с показателем. Кроме того, все показатели факторной модели должны быть количественно измеряемыми.
В зависимости от числа факторов, используемых в модели, модель может быть двух-, трех-, четырехфакторной и т. д.
Выделяют следующие виды детерминированных факторных моделей:
— аддитивная модель. Это модель, в которую факторы входят в виде алгебраической суммы

— мультипликативная модель. Это модель, в которую факторы входят в виде произведения

— кратная модель. Это модель, представляющая собой отношение факторов, то есть результативный показатель получают делением одного фактора на величину другого
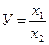
— смешанная модель. Это модели, которые сочетают в себе различные комбинации предыдущих моделей

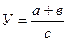

Следующим этапом проведения детерминированного факторного анализа является выбор приема факторного анализа. Существует несколько способов проведения детерминированного факторного анализа:
1. Способ цепных подстановок.Способ цепных подстановок позволяет измерить влияние каждого отдельного фактора на прирост результативного показателя. Суть способа цепных подстановок заключается в последовательной замене базисной величины каждого фактора отчетными значениями и в оценке влияния произведенной замены на результативный показатель. К достоинству этого метода относится достаточная простота и универсальность. Способ цепных подстановок можно использовать для всех видов детерминированных факторных моделей (аддитивных, мультипликативных, кратных, комбинированных).
При использовании этого способа большое значение имеет очередность расстановки факторов в факторной модели и, соответственно, последовательность изменения значений факторов, так как от этого зависит количественная оценка влияния каждого фактора.
Для метода цепных подстановок должна применяться правильно построенная детерминированная факторная модель, должна соблюдаться определенная очередность в расстановке факторов. Если в факторной модели присутствуют количественные и качественные факторы, то замену факторов следует начинать с количественного фактора.
Количественные факторы отражают количественную определенность явлений. Количественные факторы могут выражаться как в стоимостном, так и в натуральном измерителях. Например, количественные факторы характеризуют объем производства и реализации продукции, причем величина этих факторов может быть выражена как в рублях, так и в штуках, метрах и т. д.
Качественные факторы характеризуют внутренние свойства, особенности и признаки изучаемых объектов. Например, качественным фактором является жирность молока, производительность труда, качество продукции и т. д.
Алгоритм расчета способом цепной подстановки для двухфакторной мультипликативной модели выглядит следующим образом:
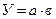
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:


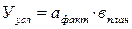
Далее определяют общее изменение результата (У):

Определяют влияние факторов:
— количественного фактора по формуле

— качественного фактора по формуле

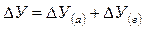
Рассмотрим алгоритм расчета на конкретном примере.
Пример 1.По исходным данным таблицы 1 определите отклонение объема производства в целом и за счет влияния факторов.
Таблица 1 – Исходные данные для факторного анализа
| Показатель | Плановое значение | Фактическое значение |
| Среднегодовая численность рабочих, чел. | ||
| Среднегодовая выработка одного работника, тыс.р. |
Решение
Составляется двухфакторная мультипликативная модель, где численность рабочих — это количественный фактор, и поэтому в модели он идет первым, а выработка — качественный фактор, и он находится за количественным.
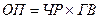
Рассчитываются плановое, фактическое и условное значения объема производства:
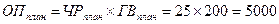
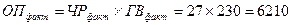
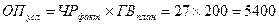
Далее определяется общее отклонение объема производства:
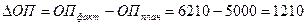
Вывод: За анализируемый период объем производства увеличился на 1210 тыс.р.
Определяется влияние численности работников и среднегодовой выработки на объем производства:
— влияние численности работников определяется по формуле:
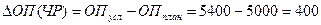
Вывод: При увеличении численности работников объем производства возрастет на 400 тыс.р.
— влияние среднегодовой выработки определяется по формуле:
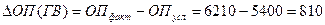
Вывод: Увеличение среднегодовой выработки одного рабочего привело к повышению объема производства на 810 тыс.р.
Проверка:
2. Способ абсолютных разниц.Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях. Его использование ограничено, но, благодаря своей простоте, он получил широкое применение в экономическом анализе. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета длямультипликативной факторной модели типа:

где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
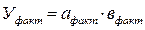

Далее определяют общее изменение результата (У):
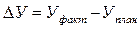
Определяют влияние факторов:
— количественного фактора по формуле
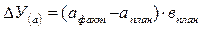
— качественного фактора по формуле
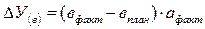
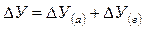
Как видно из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Рассмотрим методику расчета влияния факторов этим способом для четырехфакторной мультипликативной модели валовой продукции.
Пример 2.По исходным данным таблицы 2 определите отклонение валовой продукции в целом и за счет влияния факторов.
Таблица 2 – Исходные данные для факторного анализа
| Показатель | Плановое значение | Фактическое значение |
| Среднегодовая численность рабочих, чел. | ||
| Количество дней, отработанных одним рабочим за год, дн | ||
| Средняя продолжительность рабочего дня, ч | 8,0 | 7,6 |
| Среднечасовая выработка, тыс.р. |
Решение:
Составляется четырехфакторная мультипликативная модель:
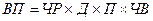
Сначала рассчитываются плановое и фактическое значение выпуска продукции:
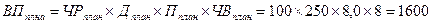
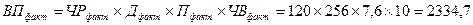
Далее определяется общее отклонение выпуска продукции:
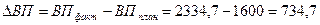
Вывод: За анализируемый период выпуск продукции увеличился на 734,7 млн.р.
Определяется влияние каждого фактора исходной модели на изменение выпуска продукции:
— влияние численности рабочих на выпуск продукции рассчитывается по формуле
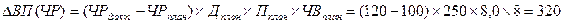
Вывод: При увеличении численности работников выпуск продукции возрастет на 320 млн.р.
— влияние количества дней, отработанных одним рабочим за год, на выпуск продукции определяется по формуле

Вывод: Увеличение числа дней, отработанных одним работником за год, привело к повышению выпуска продукции на 46,1 млн.р.
— влияние средней продолжительности рабочего дня на выпуск продукции определяется по формуле:
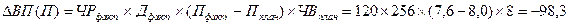
Вывод: Сокращение продолжительности рабочего дня привело к снижению выпуска продукции на 98,3 млн.р.
— влияние среднечасовой выработки на выпуск продукции определяется по формуле:
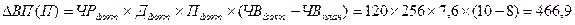
Вывод: При увеличении среднечасовой выработки выпуск продукции возрастет на 466,9 млн.р.
Проверка:
3. Способ относительных разниц.Применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это, прежде всего, касается тех случаев, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.
Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа:
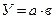
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
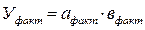
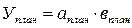
Далее определяют общее изменение результата (У):
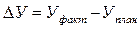
Определяют влияние факторов:
— количественного фактора по формуле
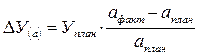
— качественного фактора по формуле
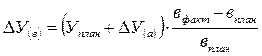
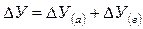
Пример 3.Закрепим рассмотренную методику на основе данных таблицы 2.
Решение.
Как и в способе абсолютных разниц, сначала определяют плановые и фактические показатели выпуска продукции:
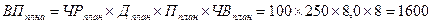
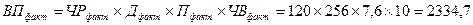
Далее определяется общее отклонение выпуска продукции:

Вывод: За анализируемый период выпуск продукции увеличился на 734,7 млн.р.
Определяется влияние каждого фактора исходной модели на изменение выпуска продукции:
— влияние численности рабочих на выпуск продукции рассчитывается по формуле
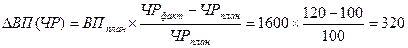
Вывод: При увеличении численности работников выпуск продукции возрастет на 320 млн.р.
— влияние количества дней, отработанных одним рабочим за год, на выпуск продукции определяется по формуле
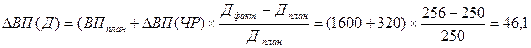
Вывод: Увеличение числа дней отработанных одним работником за год привело к повышению выпуска продукции на 46,1 млн.р.
— влияние средней продолжительности рабочего дня на выпуск продукции определяется по формуле
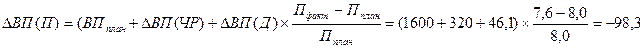
Вывод: Сокращение продолжительности рабочего дня привело к снижению выпуска продукции на 98,3 млн.р.
— влияние среднечасовой выработки на выпуск продукции определяется по формуле
Вывод: При увеличении среднечасовой выработки выпуск продукции возрастет на 466,9 млн.р.
Проверка:
4. Индексный метод.Основан на относительных показателях динамики, пространственных сравнений. Индекс показывает процентное или долевое изменение определенного значения за какой-то период времени.
Применяется этот метод только в кратных и мультипликативных, двухфакторных моделях. С помощью индексов решаются следующие задачи:
· индексы позволяют измерять изменение (динамику) сложных явлений;
· с помощью индексов можно определить влияние различных факторов на изменение уровня результативного показателя;
· индексы являются показателями сравнений не только с прошлым периодом (сравнений во времени), но с другой территорией (сравнение в пространстве), а также с нормативами, планами, прогнозами. Для факторного анализа больше подходят агрегатные индексы.
Рассмотрим методику данного метода на примере двухфакторной мультипликативной модели:
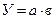
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:

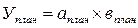
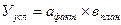
Далее определяют общее изменение результата (У):
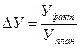
Определяют влияние факторов:
— количественного фактора по формуле
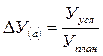
— качественного фактора по формуле
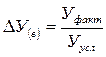
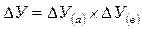
Пример 4.По данным таблицы 1 рассчитаем отклонение объема производства в целом и за счет влияния факторов.
Решение.
Составляется двухфакторная мультипликативная модель.
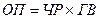
Рассчитываются плановое, фактическое и условное значения объема производства:
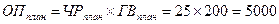

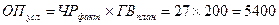
Далее определяется общее отклонение объема производства:
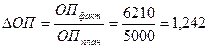
Вывод: За анализируемый период объем производства увеличился на 24,2 %.
Определяется влияние численности работников и среднегодовой выработки на объем производства:
— влияние численности работников определяется по формуле
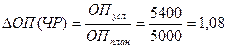
Вывод: При увеличении численности работников объем производства возрастет на 8 %.
— влияние среднегодовой выработки определяется по формуле:
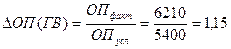
Вывод: Увеличение среднегодовой выработки одного рабочего привело к повышению объема производства на 15 %.
Проверка:
5. Интегральный метод.При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.
Рассмотрим методику интегрального метода для двухфакторной модели:
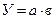
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
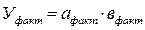
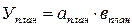
Далее определяют общее изменение результата (У):
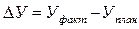
Определяют влияние факторов:
— количественного фактора по формуле

— качественного фактора по формуле

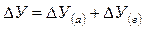
Пример 5.По данным таблицы 1 определить отклонение объема производства в целом и за счет влияния факторов.
Решение:
Составляется двухфакторная мультипликативная модель.
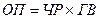
Рассчитываются плановое и фактическое значения объема производства:
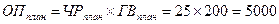

Далее определяют общее изменение результата:

Вывод: За анализируемый период объем производства увеличился на 1210 тыс.р.
Определяют влияние факторов:
— влияние численности работников на изменение объема производства определяется по формуле
Вывод: При увеличении числа работников объем производства возрастет на 430 тыс.р.
— влияние среднегодовой выработки одним работником на изменение объема производства определяется по формуле
Вывод: Увеличение среднегодовой выработки привело к повышению объема производства на 780 тыс.р.
Проверка: 430+780=12010 тыс.р.
6. Способ пропорционального деления (долевого участия).
Способ пропорционального деления относится к способам детерминированного анализа и используется для расчета влияния факторов в детерминированных аддитивных, кратно-аддитивных и мультипликативных моделях. Наиболее эффективен этот способ для определения факторов 2го, 3го и более высокого порядка.
Способ долевого участия– это модификация способа цепных подстановок. Этот метод используется для аддитивных и кратных моделей.
Сначала определяется влияние факторов 1-го порядка любым из ранее приведенных методов, а затем находится влияние факторов 2-го порядка.
Способ пропорционального деления
— влияние фактора с рассчитывается по формуле
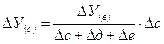
— влияние фактора д:
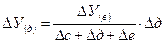
— влияние фактора е:

Способ долевого участия.
— влияние фактора с по формуле

— влияние фактора д:
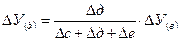
— влияние фактора е:

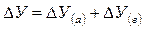
Пример 6.Производительность труда (ПТ) в текущем периоде по сравнению с прошлым снизилась на 15% из-за увеличения затрат рабочего времени (ЗРВ) на 270 чел.-ч.
При этом затраты труда на ремонтных работах (ЗТрем.раб.) увеличились на 630 чел.-ч, и снизились на перевозке грузов (ЗТпер.груз.) на 250 чел.-ч, на техническом обслуживании (ЗТтех.обсл.) — на 110 чел.-ч. Определить влияние факторов на изменение производительности труда методом пропорционального деления и долевого участия.
Решение.
Метод пропорционального деления
1. Расчет изменения производительности труда (ПТ) под влиянием изменения затрат труда на ремонтных работах (ЗТрем.раб.):
2. Изменение уровня производительности труда (ПТ) через изменение затрат на перевозки грузов (ЗТпер.груз.):
3. Динамика производительности труда ПТ в результате изменения затрат труда на техническое обслуживание ЗТтех.обсл.:
Следовательно, производительность труда в отчетном периоде снизилась по сравнению с предыдущим периодом на 15%. Увеличение затрат рабочего времени на ремонтных работах привело к снижению уровня производительности труда на 35%, а сокращение затрат времени на перевозку грузов и техническое обслуживание способствовало росту производительности труда на 13,9 и 6,1% соответственно.
Метод долевого участия
1. Влияние изменения затрат труда на ремонтных работах на производительность труда рассчитывается по формуле
2. Изменение уровня производительности труда под влиянием изменения затрат на перевозку грузов:
3. Динамика производительности труда в результате изменения затрат труда на техническое обслуживание:
Как видно из расчетов, при применении метода долевого участия получились аналогичные результаты, как и при методе пропорционального деления.
Источник