Общий способ построения линии пересечения двух плоскостей

Общий способ построения линии пересечения двух плоскостей

Контрольные задания по теме: Эпюр № 1 (вариант назначает преподаватель)

Две плоскости параллельны, когда две взаимно пересекающиеся прямые одной плоскости соответственно параллельны двум взаимно пересекающимся прямым другой плоскости.

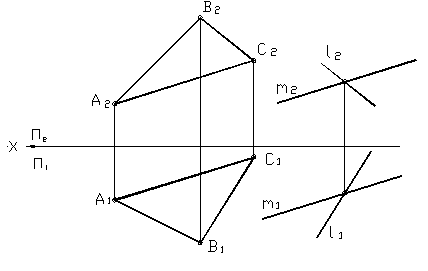
Рисунок 26

На рисунке 26 даны две плоскости. Одна задана треугольником АВС, а другая двумя пересекающимися прямыми l и m. Эти плоскости параллельны, т.к прямая l // ВС, а m // АС.

Прямая линии пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям. Для того чтобы определить общую точку, принадлежащую обеим плоскостям, вводят вспомогательную плоскость. Затем определяют линии пересечения вспомогательной плоскости и двух данных. Точка пересечения этих линий будет общей точкой плоскостей.

На практике обычно пользуются другим способом — находят точки пересечения двух прямых, принадлежащих одной плоскости с другой плоскостью, и через них проводят линию пересечения плоскостей. Возьмем для примера две плоскости в виде треугольников и построим линию их пересечения таким способом. На рисунке 27 даны две непрозрачные пластины АВС и EFG. Первая вспомогательная секущая плоскость S берется по стороне EG. Она пересекает плоскость треугольника АВС по линии 12. Строим горизонтальную проекцию линии 12 и находим точку пересечения ее со стороной EG.

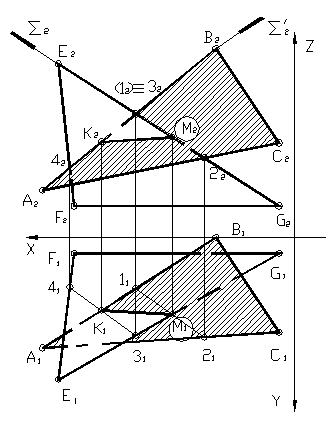
Рисунок 27

Получаем точку М – горизонтальную проекцию точки пересечения. Вторая точка К находится аналогично, путем введения вспомогательной секущей плоскости S´ по стороне АВ. Затем определяется видимость плоскостей при помощи конкурирующих точек. Для того чтобы придать чертежу наглядность, одну из пластин можно заштриховать.

1. Сформулируйте условие параллельности плоскостей.

2. Сколько можно провести плоскостей параллельных данной через какую-либо точку пространства?

3. Как решается задача на построение линии пересечения плоскостей?

4. Как определить видимость плоскостей?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L»₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L»₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L»₂.
3. Проводим прямые l’ и l» через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f_0σ и 5»=A»С»∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N» расположена на фронтальном следе f_0σ на одной линии связи с N’.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N»K» видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Источник

Общий принцип построения линии пересечения двух плоскостей общего положения

Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плос­костям, или одной точкой, принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача за­ключается в нахождении точки, общей для двух плоскостей.

Общий прием построения линии пересечения двух плоскостей заключается в следующем. Вводят вспомогательную плоскость, строят линии пересечения вспомогательной плоскости с двумя за­данными и в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

На рисунке 3 показано наглядное изображение линии пе­ресечения К₁К₂ двух плоскостей Р и Q.

Для наглядного изображения построения первой общей точки линии пересечения плос-костей P и Q (рис.4) введена вспомогательная плоскость S.С плоскостью P она пересекается по линии 1-2, с плоскостью Q – по линии 3-4.В пересечении линий 1-2 и 3-4 определена первая общая точка К₁ двух плос­костей

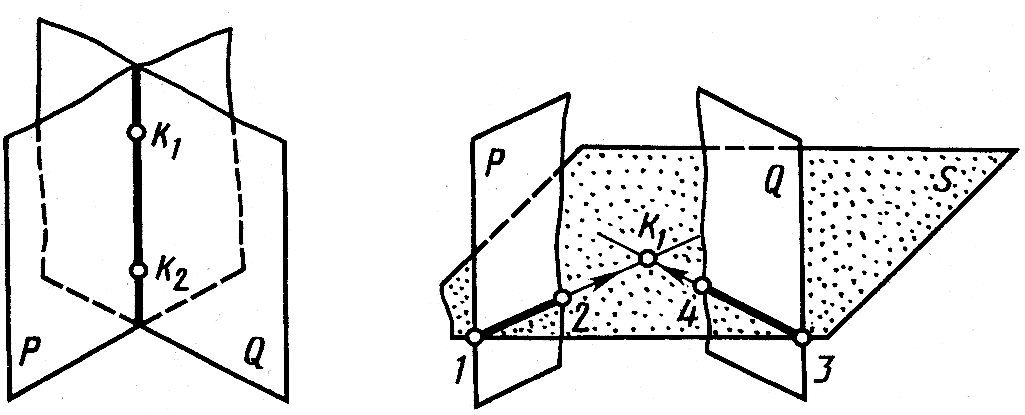
Рис. 3 Рис. 4 P и Q – первая точка линии их пе-

Вводят новую секущую плоскость и строят вто­рую точку линии пересечения.

Частный случай построения линии пересечения двух плоско­стей, когда одна из них проецирующая. Вэтом случае постро­ение линии пересечения упрощается тем, что одна ее проекция совпадает с проекцией проецирующей плоскости на ту плос­кость проекций, к которой она перпендикулярна.

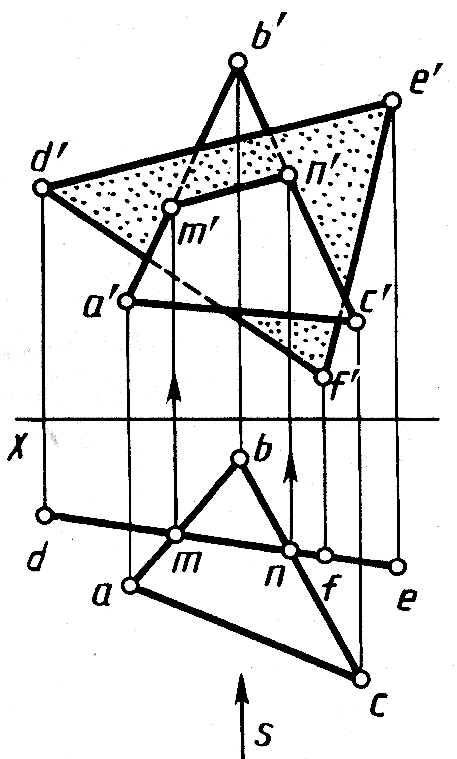
Построения линии пересечения двух тре­угольных пластин ABC и DEF, одна из которых (DEF)задана как горизонтально-проецирующая плоскость, приведен на рисунке 5.

На горизонтальной проекции в пересечении гори­зонтальных проекций ab и bc сторон ΔABC с проекцией dfe вто­рого треугольника находим горизонтальные проекции m и n точек их пересечения. По ним на фронтальных проекциях сторон a’b’ и b’c’ строим фронтальные проекции m’ и n’ точек линии пересечения MN.На фронтальной проекции отмечаем видимость ча­стей треугольников, руководствуясь следующим: при взгляде по стрелке S по горизонтальной проекции очевидно, что сторона АС находится перед плоскостью треугольника DEF. Следовательно, сторона АС иограничиваемая ею часть

Рис. 5 тре­угольника ABC до линии пересечения MN видимы (т.е. ви-

ди­ма фронтальная проекция четырехугольника a’c’n’m’).Видимая часть фронтальной проекции ΔDEF на чертеже оттенена.

Построение линии пересечения плоскостей общего положения.На рисунке 6 приведено построение проекций m’n’, mn линии пересечения двух плоскостей, одна из которых задана проекци­ями a’b’, b’c’, ab, bc двух пересекающихся прямых, другая – проекциями d’e’, f’g’, de, fg двух параллельных прямых.

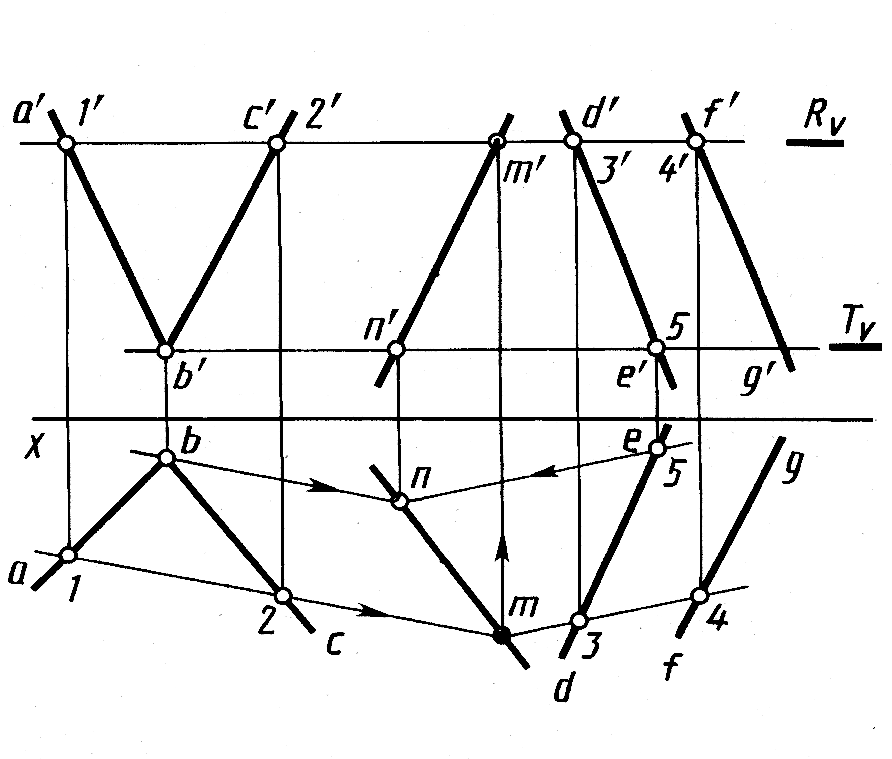
В качестве вспомогательных плоскостей взяты две горизон­тальные плоскости, заданные следами R_v и T_v.

Плоскость R пересекает первую заданную плоскость по пря­мой 1-2,вторую – по прямой 3-4.По фронтальным проекци­ям 1‘, 2′ и 3′, 4′ находим с помощью линий связи горизонтальные проекции 1, 2 и 3, 4 нагоризонтальных проекциях ab, bc, de, fg прямых. Через них проводим горизонтальные проекции линий 1-2 и 3-4 линиипересечения. Отмечаем точку m – гори­зонтальную проекцию общей точки M трех плоскостей –

Рис. 6 двух заданных и вспомогательной R.По

ней определяем фронталь­ную проекцию

m’ на фронтальном следе R_v вспомогательной плоскости.

Вспомогательные плоскости T и R параллельны. Линии их пересечения с заданными плоскостями также параллельны. Поэтому горизонтальные проекции линий пересечения плос­кости T с заданными плоскостями проведены через проекцию b параллельно проекции

1-2 и через проекцию 5 параллельно проекции 3-4.В их пересечении найдена горизонтальная про­екция n второй общей точки трех плоскостей, т. е. линии пе­ресечения двух заданных плоскостей. По ней на фронтальном следе T_v вспомогательной плоскости построена фронтальная проекция n’.Через построенные проекции m’, n’ и m, n про­водим фронтальную и горизонтальную проекции искомой ли­нии пересечения MN.

Источник

Общий способ построения линии пересечения двух плоскостей

Контрольные задания по теме: Эпюр № 1 (вариант назначает преподаватель)

Две плоскости параллельны, когда две взаимно пересекающиеся прямые одной плоскости соответственно параллельны двум взаимно пересекающимся прямым другой плоскости.

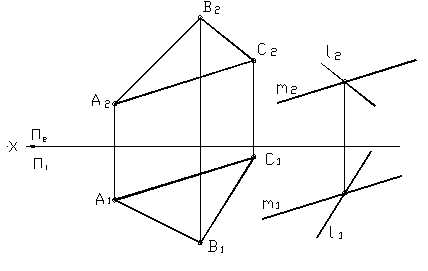
Рисунок 26

На рисунке 26 даны две плоскости. Одна задана треугольником АВС, а другая двумя пересекающимися прямыми l и m. Эти плоскости параллельны, т.к прямая l // ВС, а m // АС.

Прямая линии пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плоскостям. Для того чтобы определить общую точку, принадлежащую обеим плоскостям, вводят вспомогательную плоскость. Затем определяют линии пересечения вспомогательной плоскости и двух данных. Точка пересечения этих линий будет общей точкой плоскостей.

На практике обычно пользуются другим способом — находят точки пересечения двух прямых, принадлежащих одной плоскости с другой плоскостью, и через них проводят линию пересечения плоскостей. Возьмем для примера две плоскости в виде треугольников и построим линию их пересечения таким способом. На рисунке 27 даны две непрозрачные пластины АВС и EFG. Первая вспомогательная секущая плоскость S берется по стороне EG. Она пересекает плоскость треугольника АВС по линии 12. Строим горизонтальную проекцию линии 12 и находим точку пересечения ее со стороной EG.

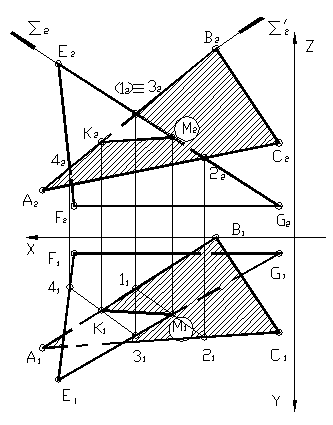
Рисунок 27

Получаем точку М – горизонтальную проекцию точки пересечения. Вторая точка К находится аналогично, путем введения вспомогательной секущей плоскости S´ по стороне АВ. Затем определяется видимость плоскостей при помощи конкурирующих точек. Для того чтобы придать чертежу наглядность, одну из пластин можно заштриховать.

1. Сформулируйте условие параллельности плоскостей.

2. Сколько можно провести плоскостей параллельных данной через какую-либо точку пространства?

3. Как решается задача на построение линии пересечения плоскостей?

4. Как определить видимость плоскостей?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник