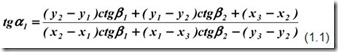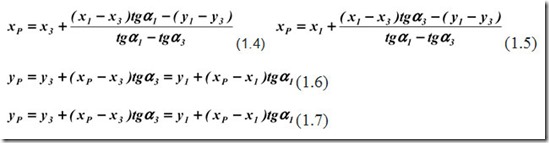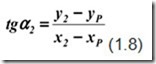Обратная геодезическая засечка способ кнейссля

Обратная угловая засечка в геодезии

Доброго времени суток, уважаемые читатели моего блога!

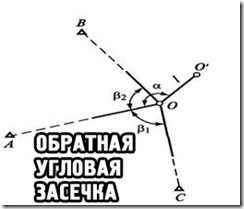
Определение положения точки посредством измерения углов (направлений) на определяемой точке, на три и более пункта с известными координатами в геодезии – это и есть обратная угловая засечка. Если исходных пунктов три – это однократная угловая засечка, если больше – многократная угловая засечка.

Французский математик Л.Потенот в 1692 году предложил математическое решение задачи по определению координат искомой точки по известным координатам трёх других точек. Сейчас решений этой задачи существует более ста. Один из видов решения – использование формул Жана Деламбра, французского геодезиста, астронома, метролога. Обратная засечка по Деламбру определяется через нумерацию исходных точек и углов по часовой стрелке с выбранным начальным направлением.

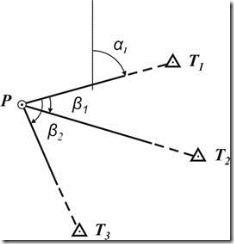
На рисунке 1 начерчена схема обратной засечки в соответствии с формулами Деламбра. Пункты триангуляции Т1, Т2, Т3 – исходные, точка (пункт) Р – определяемая, выбрано начальное направление – РТ1, на пункте Р измерены углы β1, β2 в направлении пунктов Т2, Т3.

Рис. 1. Обратная однократная угловая засечка (схема).

Сначала нужно определить дирекционный угол начального направления РТ1:

Итог: прямая угловая засечка с известными углами направлений с точки Р на исходные пункты. Известный способ определения координат Хр, Ур точки Р – это необходимое и достаточное применение формул Гаусса, которые выражаются через координаты исходных точек, вернее, их приращения:

Вычисления координат пункта Р происходит дважды; процесс вычисления, таким образом контролируется. Угол α2 высчитывается так:

Необходимо понимать, что значения α2, которое произведено по формуле 1.8, может не соответствовать значению, вычисленному по формуле 1.2 – на 180 градусов. Это связано с тем, что знаки числителя, знаменателя (формула 5.1) не могут определить приращения координат ∆х, ∆у. Контролируемое значение α2 требует определения знаков и четверти на карте проекта, где отмечены вставки точек методом обратной засечки.

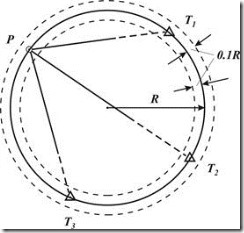
Аксиомой является то, что у обратной угловой засечки с тремя исходными пунктами нет решения, если пункт, который определяется, расположен на одной и той же окружности, что и исходные точки. Такая окружность называется «опасной». Удаление от неё определяемой точки на 0,1 х R (радиус окружности), обеспечит точность местоположения пункта, который является искомым.

Рис. 2. «Опасная» зона в обратной угловой засечке.

Если при схематичном составлении на карте (плане) обратной угловой засечки, пункт, который вычисляется, расположен в границах треугольника с вершинами – исходными пунктами (точками), можно констатировать, что «опасной окружности» здесь нет. В иных случаях, сообразно геометрическим законам, на карте (плане) строится окружность, которая проходит через 3 исходных пункта, после чего визуально определяется «опасная» зона для вычисляемого пункта.

Для работы по формулам обратной угловой засечки существует программа вычислений в режиме он-лайн, которая базируется на сайте map-info.ru. Ещё один способ определения необходимого пункта – это обратная линейно – угловая засечка. О ней поговорим в следующий раз.

На этом все друзья. Спасибо за внимание. Отличного Вам дня и хорошего настроения. Пока!!

Источник

Обратная засечка (формулы Кнейссля)

Прямая засечка (формулы Гаусса)

Если при решении задачи окажется, что видимости между исходными пунктами нет, то применяют формулы Гаусса. Для этого на пунктах А и В измеряют соответственно углы b₁ и b₂, а для контроля правильности определения координат пункта Р измеряют угол b₃ на пункте С (рисунок 17).

Измеренные углы: b₁; b₂; b₃.

Порядок решения задачи:

1. Вычисляют дирекционные углы a₁, a₂, и a₃

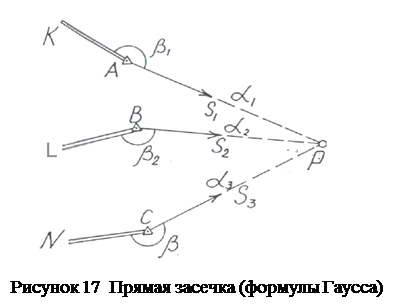
Два дирекционных угла необходимы для решения задачи, третий – для контроля и повышения точности.

2. Формулы Гаусса выводятся из известного соотношения

tg a₁ = 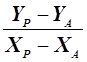(87)

Эти два равенства представляют систему двух уравнений с двумя неизвестными Х_Р и Y_P. Вычтем из уравнения (88) уравнение (89), получим

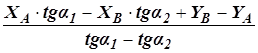
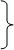
X_P = (90)

Значение ординаты вычисляют в этом случае по формулам:

Формулы Гаусса (90) и (91) служат для непосредственного вычисления значений координат пункта Р.

3. Вычтем из обеих частей равенства (90) X_A и приведя правую часть к общему знаменателю, будем иметь

X_P – Х_А = 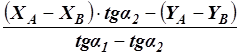(92)

Подобно этому найдем

X_P – Х_В = 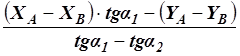(93)

Полученные два равенства вместе с равенствами (88) и (89) представляют собой формулы Гаусса для приращения координат. Вычислив их, координаты пункта Р определяют дважды:

X_P = Х_А + (Х_Р – Х_А) = Х_В + (Х_Р – Х_В)

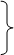
4. Используя координаты другой пары данных пунктов В и С и соответствующие им дирекционные углы a₂ и a₃, второй раз вычисляют координаты пункта Р.

Например, формулы Гаусса для непосредственных вычислений значений координат пункта Р по второй паре

X_P = 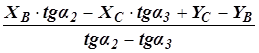(95)

Значение ординаты вычисляют в этом случае по формулам:

Y_P = Y_В + (X_P – X_В) tg a₂ или (96)

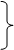
5. Оценка точности. Допустимость расхождения между значениями координат, полученными при двух решениях задачи, может быть определена по тем же формулам, что и при решении задачи по формулам Юнга.

Привязку ходов можно осуществить, решив задачу по нахождению координат пункта Р по трем исходным А, В, С (рисунок 18), расположенным на значительном расстоянии от определяемого.

Для контроля измерений производят наблюдения на пункт D. Таким образом, для решения задачи с контролем необходимо с определяемого пункта Р видеть четыре исходных пункта и измерить при определяемой точке три угла. Наиболее просто эта задача решается с использованием формул Кнейссля.

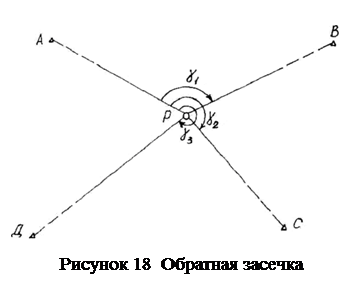
Исходные данные: Х_А, Y_A; X_B, Y_B; X_C, Y_C, X_D, Y_D.

Измеренные углы: g₁; g₂; g₃.

Порядок решения задачи:

ctgg₁ = a; ctgg₂ = b.

Из рисунка 18 видно, что a₂ = a₁ + g₁

Поэтому можно написать:

tg a₂ = tg (a₁ + g₁) = 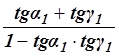(97)

2. Для сокращения записей при дальнейшем выводе перенесем начало координат в точку А. Тогда в новой системе координат будет:

3. Известно, что tg a_ВР = 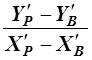(98)

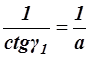
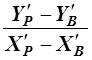
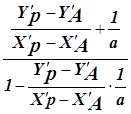
а tg g₁ = . Тогда имеем

= (99)

Так как Х¢_А = 0 и Y¢_A = 0, то получим

= ,

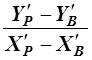
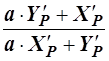
Раскрыв скобки и заново сгруппировав члены, будем иметь

(a×Y¢_В — X¢_В)× X¢_P — (a×X¢_В + Y¢_В)× Y¢_P = -( Х¢) 2 –( Y¢) 2

Обозначив коэффициенты при Х¢ и Y¢ в первом из двух равенств через К₁ и К₂, а во втором – через К₃ и К₄, будем иметь систему двух уравнений с двумя неизвестными.

I К₁ × X¢_P — К₂ × Y¢_P = — Х¢ 2 — Y¢ 2

Вычтем из первого уравнения второе, получим

(К₁ – К₃) × X¢_P -(К₂ – К₄) × Y¢_P = 0, откуда следует, что

4. Обозначим 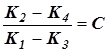(102)

тогда 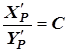или X¢_P = С × Y¢_P (103)

Подставив это выражение в уравнения I и II, получим

Y¢_P = 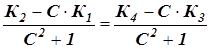(104)

5. Определив Y¢_P, находят X¢_P, подставив это значение в уравнение

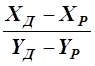
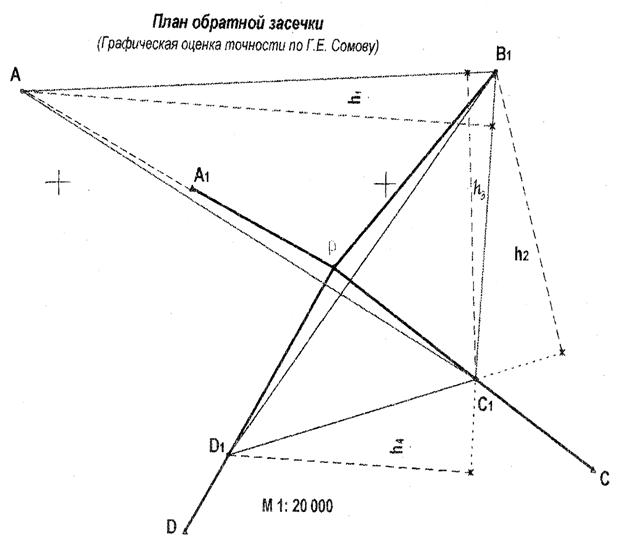
7. сtg a_РД = ; контроль a_РД — a_РА = g_{3 выч} (106)

Графическая оценка точности по формулам Г.Е. Сомова определения положения пункта Р, полученного из решения обратной засечки, производится в следующей последовательности.

По известным и полученным координатам наносят пункты А, В, С, D и Р в таком масштабе, чтобы не было направлений меньше 5 — 6 см. Измеряют расстояния от пункта Р до исходных пунктов S₁, S₂, S₃ и S₄. Вычисляют градиенты направлений по формуле q_i = 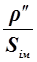; r² = 206265. В принятом масштабе градиенты откладывают от пункта Р по соответствующим направлениям, соединяют концы градиентов и получают два инверсионных треугольника _DА₁В₁С₁ и _DВ₁С₁Д₁ (рисунок 21). Из вершин А₁ и С₁ первого инверсионного треугольника проводят высоты h₁ и h₃ на противоположные стороны и измеряют их. Из вершин В₁ и Д₁ второго инверсионного треугольника аналогично находят h₂ и h₄.

Для графической оценки точности по формулам Г. Е. Сомова определяют средние квадратические погрешности положения пункта Р, полученного соответственно при первом и втором решениях:

M₁ = 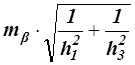; (107)

M₂ = 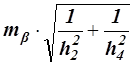; (108)

M = 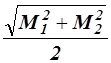; (109)

где m_b — средняя квадратическая погрешность измерения углов.

Рисунок 19 Графическая оценка точности по Г.Е. Сомову

1. Необходимые исходные данные для определения координат дополнительного пункта прямой засечкой по формулам Юнга.

2. В какой последовательности решается прямая засечка по формулам Гаусса?

3. Последовательность решения обратной засечки по формулам Кнейссля.

4. Каким образом производят определение графической оценки точности по формулам Г.Е. Сомова?

5. Напишите формулу для определения градиентов направлений.

7 УРАВНИВАНИЕ СЪЁМОЧНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ

7.1 Построение съёмочных ходов.

7.2 Уравнивание системы нивелирных ходов с одной узловой точкой

7.3 Уравнивание системы теодолитных ходов с одной узловой точкой

7.1 Построение съёмочных ходов

Съёмочные геодезические сети строят, опираясь на пункты государственной геодезической сети или сетей микротриангуляции, сетей четырехугольников без диагоналей, проложением теодолитных и мензульных ходов, различного вида засечками.

Если съёмочная сеть является самостоятельной, то не менее пятой части её пунктов закрепляют постоянными геодезическими знаками по типу грунтового или стенного полигонометрического репера. Обязательному закреплению в данном случае подлежат пункты, на которые переданы координаты, или дирекционные углы с пунктов геодезической сети высшего класса. На все пункты съёмочной геодезической сети передают высоты геометрическим или тригонометрическим нивелированием.

В камеральных вычислениях опорных геодезических сетей большое место занимает уравнивание, т.е. распределение невязок в целях получения лучших результатов и выполнения геометрических условий. При построении съёмочной сети нередко бывают случаи, когда между несколькими исходными пунктами прокладывают ходы таким образом, что все они пересекаются в одной точке, которая в таком случае называется узловой.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник