Нижеприведенные задачи решите различными способами дайте обоснование

Содержание

Решение задач различными методами и способами
Содержимое разработки
Контрольная работа по теме «Теоретико-множественный смысл суммы»
Исследовательская работа Решение текстовых задач различными способами
2.1.Алгебраический и арифметический способы решения задач на движение

Решение задач различными методами и способами

Презентация содержит приёмы работы над задачами на уроках математики в начальной школе

Содержимое разработки

Решение задач различными методами и способами

Куличенко Валентина Геннадьевна

«Славгородский педагогический колледж»

Умение решать задачу различными способами связывается с развитием гибкости мышления и играет определенную роль в развитии умственных способностей и математического мышления.

Обучение решению задач различными способами способствует более глубокому осознанию задачной ситуации, пониманию взаимосвязей между величинами, входящими в задачу, между данными и искомыми, развивает наблюдательность и математическую зоркость.

В методической литературе отмечается, что решение задачи различными способами часто бывает более полезным, чем решение одним способом нескольких задач.

При оценке разных способов решения активно используются такие умственные операции, как анализ,

что оказывает положительное влияние на развитие умственных способностей учащихся.

Методы решения задач

арифметический;
алгебраический ;
графический ;
практический ;
табличный ;
логический ;
смешанный.

основан на выборе арифметических действий, обусловленном различными связями и зависимостями между величинами, входящими в задачу, между данными и искомыми.

Задача 1. Для похода туристы закупили 96 банок консервов. В день они расходовали по 8 банок. Сколько банок консервов у них осталось после 10 дней?

Расходовали – 10 дн. по 8 б.

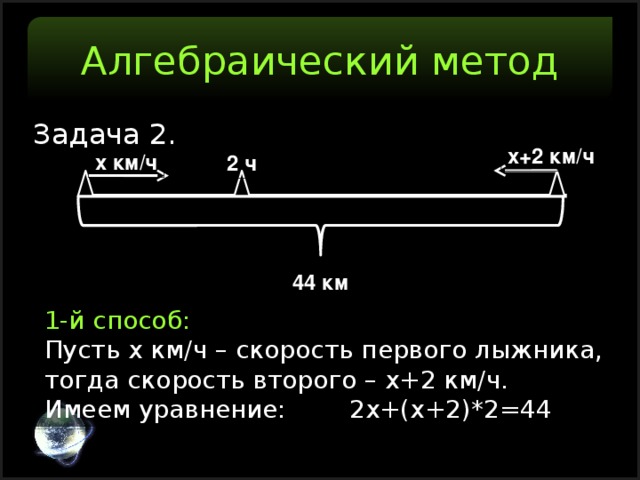
Задача 2. Из двух пунктов одновременно навстречу друг другу вышли два лыжника и через 2 ч встретились. Найдите скорость каждого лыжника, если расстояние между пунктами было 44 км, а скорость одного больше скорости другого на 2 км/ч.

Пусть х км/ч – скорость первого лыжника,

тогда скорость второго – х+2 км/ч.

Имеем уравнение: 2х+(х+2)*2=44

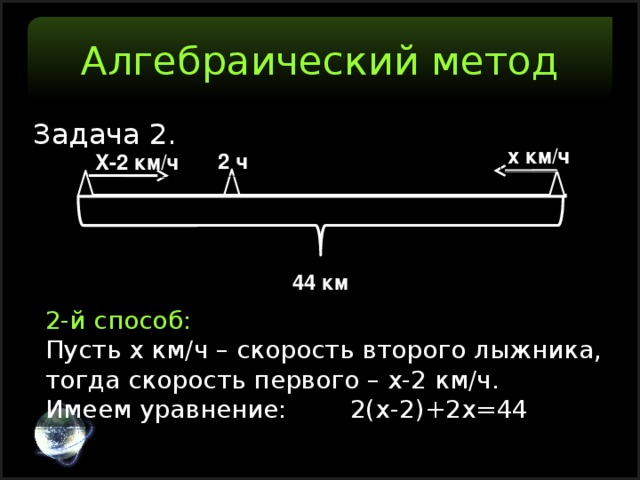
Пусть х км/ч – скорость второго лыжника,

тогда скорость первого – х-2 км/ч.

Имеем уравнение: 2(х-2)+2х=44

Задача 3. 8 яблок разложили на две тарелки. По скольку яблок на каждой тарелке?

Задача 4. Масса арбуза — 5 кг, а масса дыни на 2 кг меньше. Какова масса дыни?

Почти любую арифметическую задачу, которую решают в 1 классе, можно решить графически без выполнения арифметических действий. При этом учащиеся могут убедиться, что иногда этот подход к решению задач приводит к усложнению, а иногда позволяет легко и просто решить

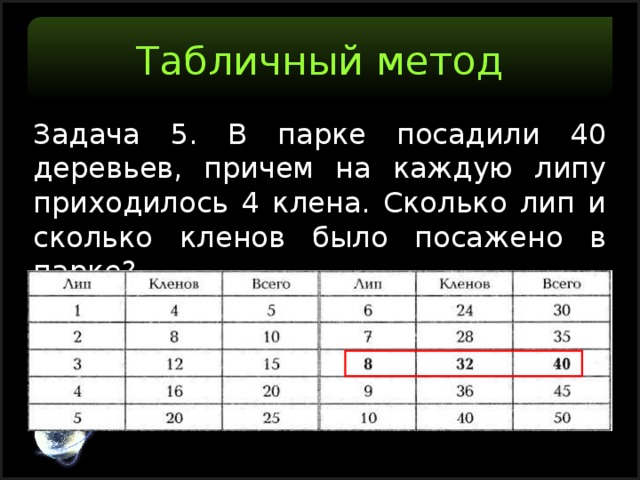
Задача 5. В парке посадили 40 деревьев, причем на каждую липу приходилось 4 клена. Сколько лип и сколько кленов было посажено в парке?

в процессе поиска решения на основе логических рассуждений можно дать ответ на вопрос задачи.

предполагает использование приемов работы по решению задач различными способами:

беседа, в процессе которой учитель подводит учащихся к тому или иному способу решения задачи;
обсуждение готовых решений — на доске учитель предлагает учащимся разные способы решения задачи и дает задание объяснить каждое выполняемое действие.

Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?

2) 600 — 450 = 150 (мин) —

60:15=4 (дет.) —
4-10=40 (дет.) —
40-30=10 (дет.) —

Источник

Контрольная работа по теме «Теоретико-множественный смысл суммы»

Контрольная работа по теме

1 . Дайте определение понятию «сумма натуральных чисел а и b » с теоретико-множественных позиций.

2. Что означает понятие «конечное множество»?

Множество, количество элементов которого конечно.

Множество, не являющееся конечным.

Множество, равномощное отрезку натурального ряда, а также пустое множество.

3. Дайте определения операциям «пересечение» и «объединение» над множествами.

4. Установите соответствие между коммутативностью, ассоциативностью сложения и их равенством

А. Коммутативность сложения

1 . (А ⋃ В) ⋃ С=А ⋃ (В ⋃ С)

Б. Ассоциативность сложения

5. Дайте определение понятию «сложение».

6. Каков теоретико-множественный смысл суммы:

7. Объясните, почему нижеприведённые задачи решается сложением

А) В ателье работали 23 портнихи, потом на работу приняли еще 12 портних. Сколько портних теперь работает в ателье?

Б) Ваня купил 35 карандашей и 12 тетрадей. Сколько всего предметов купил Ваня?

8. Найдите рациональным способом значение выражения 1755+8993+555+1607 . Укажите, какие свойства использовались.

9. Составьте задачу , которая решалась бы так : 6+8, указав какой теоретико-множественный смысл суммы.

1 . С теоретико – множественных позиций сумма натуральных чисел а и b представляет собой число элементов в объединении конечных непересекающихся множеств А и В таких, что а = n (А), b = n ( B ).

3. Пересечение множеств — это множество, которому принадлежат те, и только те элементы, которые одновременно принадлежат всем данным множествам.

Объединение множеств — множество, содержащее в себе все элементы исходных множеств.

5 . Сложение — арифметическое действие, которым находится сумма .

6. А) 9+1=10; п (А)=9, п (В)=1; А ∩ В = ; п(А ⋃ В)= п (А)+ п (В)=9+1=10;

Б) 6+0=6; п (А)=6, п (В)=0; А ∩ В = ; п(А ⋃ )= п (А)+ п ( )=6+0=6.

7. А) В данной задаче рассматривается три множества: множество А портнихи, которые работали в ателье с самого начала, множество В портнихи, которых только что приняли на работу и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как п (А)=23, п (В)=12 и А ∩ В = , то п(А ⋃ В)= п (А)+ п (В)=23+12 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи:23+12 = 35. Следовательно, теперь в ателье работает 35 портних.

Б) В данной задаче рассматривается три множества: множество А карандаши, множество В тетради и их объединение. Требуется узнать число элементов в этом объединении, а оно находится сложением. Так как п (А)=35, п (В)=12 и А ∩ В = , то п(А ⋃ В)= п (А)+ п (В)=35+12 – это математическая модель данной задачи. Вычислив значение этого выражения, получим ответ на вопрос задачи:35+12 = 47. Следовательно, Ваня купил 47 предметов.

8. 1755+8993+555+1607=(1755+555)+(8993+1607)= 2310+10600= 12910. Переместительный и сочетательный закон.

9. 6+8=14; п (А)=6, п (В)=8; А ∩ В = ; п(А ⋃ В)= п (А)+ п (В)=6+8=14.

Источник

Исследовательская работа Решение текстовых задач различными способами

Республиканская открытая конференция научного объединения учащихся «Сигма»

Тема: «Различные способы решения текстовых задач»

ученик 10 класса МОУ СОШ№1

Дугулубгова Фатимат Султановна,

учитель математики высшей категории

МОУ СОШ№1 с.п.В.Куркужин

2. Алгоритмизация текстовых задач ………………………………………………..4

2.1. Алгебраический и арифметический способы решения текстовых задач……5

2.2.Графический способ решения текстовых задач ……………………………….7

3. Задачи на совместную работу ……………………………………………………9

Известно, что исторически долгое время математические знания передавались из поколения в поколение в виде списка задач практического содержания вместе с их решениями. Первоначально обучение математике велось по образцам. Ученики, подражая учителю, решали задачи на определённое «правило». Таким образом, в давние времена обученным считался тот, кто умел решать задачи определённых типов, встречавшихся в практике.

Но сейчас решениям задач уделяется достаточно много внимания в школе. Умение решать задачи современный человек независимо от рода деятельности и уровня образования нуждается непрерывно.

Кроме того, разнообразные способы решения будят фантазию, позволяют организовать поиск решения каждый раз новым способом. Тем более, статистика сдачи ЕГЭ и ОГЭ показывает, что большинство учащихся не справляются с текстовыми задачами.

Актуальность данной работы можно обобщить тем, что с помощью текстовой задачи формируются важные умения, связанные с анализом текста, выделением главного в условии, составлением плана решения, проверкой полученного результата. В ходе решения текстовой задачи формируется умение переводить ее условие на математический язык уравнений, систем, графических образов, т.е. составлять математическую модель. Исходя из вышесказанного, мы делаем следующие выводы: Объект исследования : различные способы решения задач; Предмет исследования: блок текстовых задач по математике; Цель исследования : рассмотрение текстовых задач и применение к их решению арифметического, алгебраического, графического способов решения; Задачами для реализации цели исследования являются разбор и решение текстовых задач из ОГЭ и ЕГЭ. Методы исследования : практико-поисковый, анализ и классификация типов текстовых задач. Предполагаемые продукты: т ипология задач и методы их решения, разработка методики решения текстовых задач, используемых в ОГЭ и ЕГЭ. Конечный результат : успешная сдача ОГЭ и ЕГЭ Гипотеза: многие считают, что текстовые задачи нельзя решить легко, но так ли это на самом деле.

2. Алгоритмизация текстовых задач

В школьном курсе математики решение текстовых задач считается одним из самых сложных для восприятия и усвоения разделов. Это объясняется в значительной степени тем, что если задачи другого рода требуют от своего решения формально-технического аппарата, применение которого алгоритмизировано, то решение текстовых сюжетных задач требует от нас еще и этапа составления уравнения или системы уравнений, понимания имеющихся в задаче условий и перевода их на математический язык. И этот этап в большей степени, чем все остальные носит эвристический характер. Чтобы облегчить данную работу нужно рассматривать любую текстовую задачу как систему, в независимости от того, является ли она задачей на движение, на работу и т.д.

Итак, для того, чтобы рассматривать задачу как систему, нам необходимо определить: элементы задачи; характер взаимосвязей между элементами. Первый набор элементов, который необходимо определить в задаче как системе – это участники контекста задачи (машина и велосипед, поезда, амфибии и самолеты; рабочие и землеройки, станки и роботы и т. д.) Уравнения, которые составляются на основании условий задач на движение, как правило, содержат такие величины, как скорости движущихся объектов, расстояние, время, ускорение, а также скорость течения воды (движение по реке).

Решая задачи для различных типов движения нам необходимо определить некоторые особенности.

Для равномерного движения по прямой будут характерны следующие особенности:

1) Движение на отдельных участках считается равномерным, а пройденный путь определяется по формуле , где — скорость, — время.

2) Скорость считается всегда величиной положительной.

3) При движении объекта по течению реки, скорость течения которой равна , а собственная скорость объекта в стоячей воде равна , скорость объекта по течению реки относительно берега будет равна . При движении объекта против течения реки, его скорость относительно берега будет равна , при этом должно выполняться неравенство .

4) Когда в условии задачи говорится о движении плотов, то можно считать, что плот имеет ту же скорость, что и течение реки.

Исследовав типы задач для различных типов движения из Открытого банка задач ЕГЭ по математике, мы можем разделить их на группы – задачи на движение в одном направлении, задачи на встречное движение и движение туда и обратно, и составить для каждой группы одну общую модель решения данных задач.

2.1.Алгебраический и арифметический способы решения задач на движение

В задачах на движение за неизвестную величину чаще всего, за неизвестную наиболее рационально принимать наименьшую из величин или то, что необходимо найти. При этом не стоит забывать о том, что нам необходимо указать дополнительное условие, т. е. например, если это скорость, то она не может быть отрицательной или равной нулю. Для решения задач достаточно правильно составить таблицу:

Скорость

Источник