Нестандартные способы запоминания таблицы умножения
Содержимое разработки
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
«УЛЬЯНОВСКИЙ ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ»
МДК 01.04 Теоретические основы начального курса математики с методикой преподавания
Нетрадиционные способы (приемы) запоминания таблицы умножения
Специальность 44.02.02 Преподавание в начальных классах
очное обучение
Студентка 2 курса 203 группы
Медянникова Олеся Станиславовна
Прием внешней опоры
В качестве опоры используется рисунок или прямоугольная таблица чисел.
Детям, которые обладают плохой механической памятью, можно на первых порах предложить использовать клетчатое поле тетради.
Обводя на клетчатом поле прямоугольник с заданным количеством клеток в сторонах, ребенок использует эту модель для контроля полученного результата или просто подсчитывает клетки как умеет.

Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы умножения числа 4.
Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чемпять.
На двух руках отогнуто три пальца — это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.
Китайский способ умножения
Такой прием напоминает умножение столбиком, но проводится довольно долго.
Использование приема. Допустим, нам надо умножить 4 на 5. Начертим следующий рисунок:
Теперь нужно сосчитать пересечения линий( 4*5=20, 20 точек пересечений)
Запоминание умножения на 9
Заменяют умножением на 10 минус число, которое умножаем.
Например: 4 х 9 = 4 х10 — 4 = 36
Мнемонические приёмы при заучивании таблицы умножения.
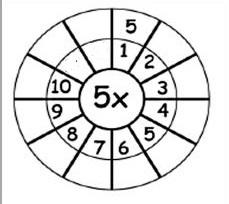
Это могут быть карточки с записями табличных случаев, которые ребёнок носит в кармане и просматривает при любом удобном случае.В самом центре — первый множитель (число изучаемое в таблице умножения), вокруг него написаны возможные вторые множители (от 1 до 10). В наружном кольце необходимо обозначить соответствующий результат умножения.
Русский крестьянский способ
запишем числа на одной строчке;
левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
деление заканчивается, когда слева появится единица;
вычёркиваем те строчки, в которых стоят слева чётные числа;
далее оставшиеся справа числа складываем – это результат.
Этот способ подойдет детям, склонным к запоминанию стихов.
Итак, на старт выходит ДВОЙКА!
Умножив два на единицу,
Получим ДВОЙКУ — лебедь-птицу,
Спасает каждый ученик
От этих «птичек» свой дневник.
Известно детям в целом мире,
Что дважды два равно ЧЕТЫРЕ.
Им также следует учесть,
Что дважды три получим ШЕСТЬ.
Два на четыре — будет ВОСЕМЬ.
И всех ребят мы очень просим
Забыть капризы, ссоры, лень
Восьмого марта — в мамин день!
Нам два на пять умножить нужно,
И если все возьмёмся дружно,
Да поднатужимся, ребятки,
То сразу попадем в ДЕСЯТКУ! …
Чтобы умножать на 4, можно просто дважды удваивать число. Например, чтобы умножить 6 × 4, нужно удвоить 6 два раза: 6 + 6 = 12, 12 + 12 = 24.
Предложить детям пофантазировать и представить, с чем у них ассоциируются цифры от 1 до 9.
Попросить детей нарисовать ассоциации. Главное, чтобы эти образы были придуманы детьми.
Далее нужно закрепить эти ассоциации, для этого вразброс показывайте вашему ученику нарисованные им картинки.
Потом вместе сочините историю на каждый пример умножения.
В частности, 2*3=6. Одна девочка придумала рассказ: «Гулял как-то лебедь (2), встретил сердечко (3) и влюбился в него. Стал он ухаживать за сердечком. Увидел это клоун (6) и стал дразнить их: «Тили-тили-тесто, жених и невеста».
Умножение на 10
Все примеры на 10 оканчиваются на 0, а начинаются с числа, на которое мы умножаем.
Источник
Нетрадиционные способы умножения многозначных чисел
Краткая аннотация исследовательской работы
Каждый школьник умеет умножать многозначные числа «столбиком». В данной работе автор обращает внимание на существование альтернативных способов умножения, доступных младшим школьникам, которые могут «нудные» вычисления превратить в весёлую игру.
В работе рассматриваются шесть нетрадиционных способов умножения многозначных чисел, используемые в различные исторические эпохи: русский крестьянский, решетчатый, маленький замок, китайский, японский, по таблице В.Оконешникова.
Проект предназначен для развития познавательного интереса к изучаемому предмету, для углубления знаний в области математики.
Оглавление
Введение 3
Глава 1. Альтернативные способы умножения 4
1.1. Немного истории 4
1.2. Русский крестьянский способ умножения 4
1.3. Умножение способом «Маленький замок» 5
1.4. Умножение чисел методом «ревность» или «решётчатое умножение» 5
1.5. Китайский способ умножения 5
1.6. Японский способ умножения 6
1.7. Таблица Оконешникова 6
1.8.Умножение столбиком. 7
Глава 2. Практическая часть 7
2.1. Крестьянский способ 7
2.2. Маленький замок 7
2.3. Умножение чисел методом «ревность» или «решётчатое умножение» 7
2.4. Китайский способ 8
2.5. Японский способ 8
2.6. Таблица Оконешникова 8
2.7. Анкетирование 8
Заключение 9
Приложение 10
«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».
Б. Паскаль
Введение
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе. Возник вопрос: а есть ли еще какие-нибудь альтернативные способы вычислений? Мне захотелось изучить их более подробно. В поисках ответа на возникшие вопросы было проведено данное исследование.
Цель исследования: выявление нетрадиционных способов умножения для изучения возможности их применения.
В соответствии с поставленной целью нами были сформулированные следующие задачи:
— Найти как можно больше необычных способов умножения.
— Научиться их применять.
— Выбрать для себя самые интересные или более легкие, чем те, которые предлагаются в школе, и использовать их при счете.
— Проверить на практике умножения многозначных чисел.
— Провести анкетирование учащихся 4-х классов
Объект исследования: различные нестандартные алгоритмы умножения многозначных чисел
Предмет исследования: математическое действие «умножение»
Гипотеза: если существуют стандартные способы умножения многозначных чисел, возможно, есть и альтернативные способы.
Актуальность: распространение знаний об альтернативных способах умножения.
Практическая значимость. В ходе работы было решено множество примеров и создан альбом, в который включены примеры с различными алгоритмами умножениями многозначных чисел несколькими альтернативными способами. Это может заинтересовать одноклассников для расширения математического кругозора и послужит началом новых экспериментов.
Источник
Доклад «Нетрадиционные способы изучения таблицы умножения»
Нетрадиционные способы изучения таблицы умножения
С 2011 года во всех школах Российской Федерации введен Федеральный государственный образовательный стандарт начального общего образования (ФГОС НОО). Основное отличие этого стандарта связано с требованиями к результатам обучения. Стандарт устанавливает требования к результатам обучающихся, освоивших основную образовательную программу начального общего образования:
личностным, включающим готовность и способность обучающихся к саморазвитию,.
метапредметным, включающим освоенные обучающимися универсальные учебные действия (познавательные, регулятивные и коммуникативные), обеспечивающие овладение ключевыми компетенциями, составляющими основу умения учиться
предметным, включающим освоенный обучающимися в ходе изучения учебного предмета опыт специфической для данной предметной области деятельности по получению нового знания, его преобразованию и применению
Основным требованием к предметным результатам при обучении математике является знание таблицы умножения однозначных чисел и соответствующих случаев деления на уровне автоматизированного навыка.
Прочные знания, умения и навыки учащиеся приобретают в процессе активной познавательной деятельности, важнейшей предпосылкой которой является интерес .
Как донести учебный материал до сознания учащихся? Как развить их активную познавательную деятельность, чтобы дети могли овладеть знаниями, умениями и навыками? Как вызвать у учащихся положительное отношение к учебе, помочь им превратить знания в убеждения? Как научить всех: и тех, кто учится с интересом, и тех, у кого его нет? Эти вопросы учителю приходится решать каждый день при подготовке урока. Все они так или иначе связаны с поисками наиболее продуктивных методов обучения. Что же принято понимать под методами обучения? Методы обучения — это способы совместной деятельности учителя и учащихся, направленные на решение задач обучения.
Как известно, стойкий познавательный интерес формируется при сочетании эмоционального и рационального. Ещё К.Д. Ушинский подчёркивал, как важно серьёзное занятие сделать для детей занимательным.
Для некоторых детей заучивание таблицы умножения трудностей не представляет — в этом возрасте механическая память хорошо развита. Но вот тем школьникам, у которых преобладает образная и эмоциональная память, заучивание таблицы умножения время дается нелегко. Как помочь им быстро выучить таблицу умножения?
Первый шаг глубокого, осмысленного понимания — это раскрытие конкретного смысла действия умножения, осознание связи умножения с уже хорошо знакомым действием сложения. А для этого мало таких заданий, как «замени сумму произведением чисел», «замени произведение суммой чисел». Они в меньшей степени побуждают мыслить ребёнка. Творческая деятельность, гибкость мышления возможны в нестандартных условиях, об этом следует помнить учителю и предлагать такие задания, при решении которых необходим самостоятельный перенос знаний и способов действий в новое условие, использование их в новых ситуациях. Задача учителя: поставить своей целью — вызвать заинтересованность детей, помочь им увидеть закономерности — «секреты» таблицы умножения.
Как известно, таблица умножения в учебниках 3 – 4 классах дается как таблица Пифагора.
Много, непонятно и страшно. На самом деле, таблица только с виду кажется необъятной, отдельные ее строки и столбцы можно запомнить очень легко.
Когда начинается изучение табличного умножения я предлагаю рассмотреть «таблицу в таблице»
Для начала разбираемся с умножением на единицу: здесь и запоминать ничего, ведь число, умноженное на единицу, равно самому себе. Потом можно смело зачеркнуть колонку и строку с умножением на десять: достаточно объяснить, что к полученному числу нужно приписать ноль. И вот таблица уже сократилась на 20 примеров и стала не такой страшной. Во вторых: начинаем внимательно смотреть, и видим, что таблица симметричная .
Ведь 4*8=8*4, a 9*6=6*9, и так далее. Чтобы все не перечислять, запишем это наблюдение словами:
Если одно число умножить на второе, то ответ такой же, как если второе число умножить на первое (переместительное свойство умножения).
То есть часть таблицы нам дается «совершенно бесплатно»! А какая часть? Если сказали «половина», почти угадали. Благодаря переместительному свойству умножения, таблица сокращается почти в 2 раза!
Это приободряет ребят. Не забываю при этом сказать, что во времена Пифагора (470-500 лет назад) совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы , даже если он окончил европейский университет. И, конечно, обещаю поделиться своими «секретами», которые помогут им быстро запомнить таблицу . Это тоже стимул для того, чтобы превзойти в 9-10-летнем возрасте современников Пифагора.
Я уже давно стала думать над тем, как упростить изучение, как помочь детям освоить таблицу умножения, как подарить детям крепкие знания и спасти школьные дневники от двоек.
Метод, который я предлагаю ,конечно же, не панацея, но он проверен и
работает. Суть его в том, чтобы ребёнок без нервов, не напрягаясь , а просто и незаметно для себя выучил таблицу умножения.
Из многолетнего опыта работы я поняла, что проще выучить таблицу
умножения путем простого повторения записи суммы одинаковых слагаемых.
Когда и как это делать? А всё очень просто. Я использую для этого минутки чистописания. Одним выстрелом так сказать, убиваю двух зайцев. Во-первых, не надо прописывать цифры в тетрадях учеников, на которые ,кстати, они обращают мало внимания ,не пишут их, или пишут как попало и такая работа не даёт никакого результата. Во-вторых, при такой форме проведения минутки чистописания у детей активно работает мозг: они не просто механически прописывают цифры ,но и складывают их ,прежде чем написать.
Алгоритм записи прост (для этого предлагаю ребятам найти закономерность и продолжить числовой ряд):2 4 6 8 10 12 14 16 18 20.,т.е каждое следующее число получается путём прибавления к предыдущему числу того самого первого числа, с которого и начали сложение. А что в результате получается? А получается та самая таблица умножения, которую предстоит им заучивать. Но дети этого пока не знают. Они просто каждый день пишут красиво в тетрадях минутку чистописания. Каждый урок математики у меня начинается с минутки чистописания.
Но вот наступает время изучения таблицы на 2. Дети прописывают данную минутку чистописания, а число 2,на которое увеличивается каждое последующее, записываем на полях, записав ее зеленой ручкой. Далее коллективно заполняют привычную таблицу умножения на 2 и соответствующие случаи деления. И вот тут я раскрываю «секрет» минутки чистописания. Предлагаю написать над каждым числом числа от 1до 10 зеленой ручкой, а потом предлагаю найти закономерность в этой записи. Многие ученики практически сразу замечают, что верхняя строка – это первый множитель, а числа нижней строки – это произведение. Остается лишь обратить внимание на число 2, и получилась таблица умножения, только не такая длинная и пугающая, которую мы записали ранее. Из этой записи легко выводится и таблица на деление.
Источник