Нестандартные способы сравнения дробей

Презентация на тему: «Нестандартные способы сравнения дробей.»

Презентация содержит подборку заданий на тему: «Нестандартные способы сравнения дробей». Материал удобен для работы на уроке. В нем описаны методы и подобраны задания на каждый из них. Имеются так же обобщающие задания для самостоятельного выполнения.

Просмотр содержимого документа
«Презентация на тему: «Нестандартные способы сравнения дробей.»»

Нестандартные способы сравнения дробей

5класс, урок № 93

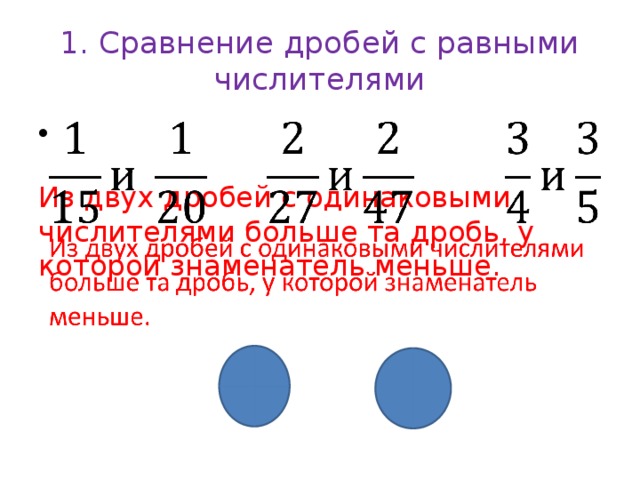
1. Сравнение дробей с равными числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

2. Сравнение с единицей

3. Сравнение с половиной

4.Сравнение с третью

5. Сравнение остатков до единицы

• и

Источник

Частные приемы сравнения обыкновенных дробей
презентация урока для интерактивной доски по алгебре (6 класс) на тему

Презентация используется на уроке по теме «Сравнение обыкновенных дробей». Будьте внимательны — в файле множество гиперссылок. От правильности ответа (и, соответственно, правильного клика на число, являющееся ответом) зависит последовательность показа слайдов.

Скачать:

Вложение	Размер
Частные приемы сравнения обыкновенных дробей	837.82 КБ

Предварительный просмотр:

Подписи к слайдам:

частные случаи сравнения обыкновенных дробей Гимназия 32 г.Иваново Учитель математики Иванова А.С.

Найдите наименьшее общее кратное следующих чисел, и откройте портрет великого математика.

НОК (15 ; 5) ? 15 21 5 30 35 45 75 1

НОК (8 ; 9) ? 81 24 9 198 8 3 72 116

НЕТ, НЕПРАВИЛЬНО! 72

НОК (8 ; 9) ?? 81 24 9 198 8 3 72 116

НА ЭТОТ РАЗ ТОЧНО. 72

И СНОВА – НЕТ! 72

НОК (6 ; 12) ? 12 6 24 17 33 9 120 36

АБСОЛЮТНО ВЕРНО. 12

ДА НЕТ ЖЕ – 12! 12

НОК (6 ; 12) ?? 12 6 24 17 33 9 120 36

ОПЯТЬ ОШИБКА! 12

НОК (6 ; 12) . 12 6 24 17 33 9 120 36

ДУМАЙТЕ КАК СЛЕДУЕТ! 12

НОК (6 ; 12) . 12 6 24 17 33 9 120 36

ДА ЧТО С ВАМИ? 12

НОК (12 ; 15) ? 32 3 24 1215 15 12 125 60

СКОРО ОТКРОЕТЕ ПОРТРЕТ! 60

НОК (12 ; 15) ?? 32 3 24 1215 15 12 125 60

НЕПЛОХО СЧИТАЕТЕ! 60

НУ ВОТ, ОПЯТЬ! 60

НОК (12 ; 15) . 32 3 24 1215 15 12 125 60

ЧТО-ТО МЫ УВИДИМ! 60

БЕЗ КОММЕНТАРИЕВ! 60

НОК (12 ; 15) . 32 3 24 1215 15 12 125 60

УРА, СВЕРШИЛОСЬ! 60

НЕТ, НЕТ И НЕТ. 60

НОК (12 ; 15) . 32 3 24 1215 15 12 125 60

И СНОВА ВЕРНО! 60

НОК (12 ; 15) . 32 3 24 1215 15 12 125 60

ЗАБУДЬТЕ ПРО ОШИБКУ! 60

ЧЕРНАЯ ПОЛОСА! 60

НОК (12 ; 15) . 32 3 24 1215 15 12 125 60

МОЖЕМ УВИДЕТЬ ПРОФИЛЬ! 60

СТАНОВИТСЯ ГРУСТНО! 60

НОК (12 ; 15) … 32 3 24 1215 15 12 125 60

ШАНСЫ ЕЩЕ ЕСТЬ! 60

ПЛОХО, СОВСЕМ ПЛОХО! 60

НОК (6 ; 4) ? 2 12 24 6 3 64 46 67

НОК (6 ; 4) ?? 2 12 24 6 3 64 46 67

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

ОСТАЛОСЬ 1 ЗАДАНИЕ! 12

БУДЬТЕ ВНИМАТЕЛЬНЕЕ! 12

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

ЭХ, НЕ ПОВЕЗЛО! 12

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

НЕЛЬЗЯ НЕ СОГЛАСИТЬСЯ! 12

ПОЛОСА НЕВЕЗЕНИЯ?! 12

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

В ЦЕЛЬ, ОТЛИЧНО! 12

А ЕСЛИ ПОДУМАТЬ! 12

НОК (6 ; 4) .. 2 12 24 6 3 64 46 67

У ВАС ЕЩЕ ЕСТЬ ШАНСЫ! 12

ОЧЕРЕДНАЯ ОШИБКА! 12

НОК (6 ; 4) … 2 12 24 6 3 64 46 67

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

СКОРО ОТКРОЕМ КАРТИНКУ 12

И КАК ВЫ ГОТОВИЛИСЬ? 12

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

ОЧЕРЕДНАЯ ОШИБКА. 12

НОК (6 ; 4) . 2 12 24 6 3 64 46 67

НОК (6 ; 4) 2 12 24 6 3 64 46 67

ДАЛЬШЕ СМЫСЛА НЕТ… 12

НОК (12 ; 9) ? 276 12 9 3 36 63 24 55

НУ ВОТ! ТЕПЕРЬ ГАДАЙТЕ. 36

НОК (12 ; 9) ?? 276 12 9 3 36 63 24 55

НУ И КТО ЭТО? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

ИТАК, КТО ЭТО? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

ЧТО Ж, НЕПЛОХО ? 36

ПРАВДА, ОБИДНО? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

ДУМАЮ, ДОГАДАЛИСЬ ? 36

УЗНАТЬ НЕПРОСТО. 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

СМОЖЕТЕ УЗНАТЬ ? 36

НОК (12 ; 9) .. 276 12 9 3 36 63 24 55

ПОПРОБУЙТЕ УЗНАТЬ ? 36

НОК (12 ; 9) … 276 12 9 3 36 63 24 55

И КТО ЖЕ ЭТО ? 36

НОК (12 ; 9) …. 276 12 9 3 36 63 24 55

СЛАБЫЙ РЕЗУЛЬТАТ. 36

НОК (12 ; 9) ?. 276 12 9 3 36 63 24 55

КТО ЭТОТ ЧЕЛОВЕК ? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

ИТАК, КТО ЖЕ ЭТО? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

МОЖНО УЗНАТЬ ? 36

УЗНАТЬ НЕРЕАЛЬНО? 36

НОК (12 ; 9) . 276 12 9 3 36 63 24 55

ПОПРОБУЙТЕ УЗНАТЬ. 36

НОК (12 ; 9) 276 12 9 3 36 63 24 55

ПРАВИЛЬНОЕ РЕШЕНИЕ. 36

НУ И КТО ЖЕ ЭТО? 36

НОК (12 ; 9) ……. 276 12 9 3 36 63 24 55

У ВАС ЕСТЬ ШАНС. 36

приведение дробей к общему знаменателю

приведение дробей к общему знаменателю сравнение дробей с общим знаменателем

к о с м о г н а т у с

приведение дробей к общему знаменателю сравнение дробей с общим знаменателем сравнение дробей с одинаковым числителем

приведение дробей к общему знаменателю сравнение дробей с общим знаменателем сравнение дробей с одинаковым числителем приведение дробей к одинаковому числителю

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. 2. 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. 2. 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. 2. 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. 2. 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2. 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2.Сравнить с ½ 3. 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2.Сравнить с ½ 3. Определить близость к 1 b – a = d – c 4.

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2.Сравнить с ½ 3. Определить близость к 1 b – a = d – c 4. Общее правило

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2.Сравнить с ½ 3. Определить близость к 1 b – a = d – c 4. Общее правило

Частные приемы сравнения обыкновенных дробей Что делать? Условие Примеры 1. Сравнить с единицей 2.Сравнить с ½ 3. Определить близость к 1 b – a = d – c 4. Общее правило

ЗАДАНИЕ 4 Сравнить дроби наиболее удобным способом:

Источник

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Произвести сравнение заданных дробей 65 126 и 87 126 .

Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

• найти общий знаменатель;
• сравнить дроби.

Рассмотрим данные действия на примере.

Произвести сравнение дробей 5 12 и 9 16 .

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48 : 12 = 4 , для второй дроби 9 16 – 48 : 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48 27 48 . Значит, 5 12 меньше 9 16 .

Ответ: 5 12 9 16 .

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями: если a · d > b · c , тогда a b > c d , но если a · d b · c , тогда a b c d . Рассмотрим сравнение с разными знаменателями.

Произвести сравнение дробей 5 18 и 23 86 .

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.

Необходимо выполнить сравнение 63 8 и 9 .

Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63 72 , тогда получаем 63 8 72 8 . Значит, заданная дробь меньше целого числа 9 , то есть имеем 63 8 9 .

Источник

Мастер-класс: «ХИТРЫЕ» СПОСОБЫ СРАВНЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

Муниципальное бюджетное общеобразовательное «Лицей №4» г.о.Коломна

Конспект мастер — класса

тема

«ХИТРЫЕ» СПОСОБЫ СРАВНЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

Заместитель директора по УВР, учитель математики I категории

Ташпулатова Ноила Разимовна

Цели: 1. Формировать способности к построению и использованию

алгоритма сравнения обыкновенных дробей: а) способом

дополнения до 1; б) способом сравнения с промежуточным

Повторить и закрепить: приведение дробей к наименьшему общему числителю, знаменателю, сравнение дробей с одинаковыми числителями и знаменателями, алгоритм сравнения правильных и неправильных дробей, сокращение дробей.

Тип урока: «Открытие» нового знания.

Эпиграф: « Единственный путь, ведущий к

Ход урока: 1.Организационный момент.

Здравствуйте, уважаемые коллеги! Я рада видеть Вас на своём мастер —

классе и надеюсь на взаимное сотрудничество, которое верю, доставит

удовольствие, как мне, так и Вам.

2. Актуализация знаний.

— Открыли тетради, записали число, классная работа.

— запишите их в порядке возрастания

— Каким способом сравнения Вы воспользовались?

— Какие дроби надо прибавить к каждой из этих дробей, чтобы в сумме

получилась единица?

— Какими по отношению к единице являются все использованные нами

— А как из этих дробей получить неправильные?

— Какими они будут по сравнению с 1?

— Сформулируйте правило сравнения правильных и неправильных дробей.

— Приведите дроби последнего ряда к наименьшему общему знаменателю и

запишите их в порядке убывания.

— Сформулируйте правило сравнения, которое Вы применили в этом случае.

— Какая из этих дробей будет лежать на числовом луче правее всех, какая –

— Сформулируйте правило сравнения дробей с помощью числового луча.

Итак, какие способы сравнения обыкновенных дробей мы с Вами повторили?

( Фиксирую на античном сосуде названные способы сравнения).

3. Постановка учебной задачи.

— Сравните дроби и дайте объяснение полученному результату:

( Выполняют задание индивидуально в тетрадях в течение 3 – 4 минут).

По истечении времени проверяем выполненную работу с проговариванием способа сравнения.

— На какой паре дробей возникло затруднение и почему?

— Так какая же возникла перед нами задача?

— А как бы Вы сформулировали тему нашего урока?

Из предложенных вариантов выбираем, подходящее и записываем в тетрадях.

(Возможные варианты: Дополнительные, «хитрые», новые и т.д.

способы сравнения обыкновенных дробей.)

— Повторите ещё раз поставленную на сегодняшний урок задачу.

4. «Открытие» нового знания.

— Чтобы проверить, насколько Вы оказались правы в своих предположениях в 3 и 4 примерах, Вам предлагается выполнить следующие задания:

— представьте частные 8 : 12; 12 : 16; 16 : 20; 20 : 24 в виде несократимых дробей.

— Что интересного Вы заметили в полученном ряду дробей?

— Назовите следующие три дроби.

— Какая дробь стоит на 34 месте? А на 999?

— Предположите, в каком порядке расположены дроби в этом ряду и почему?

— Тогда какой знак сравнения Вы бы поставили между дробями ?

— А как обосновать высказанное предположение?

— Дополните каждую из дробей до 1.

— А легко ли сравнить полученные сравнения?

— Верно, ли было наше предположение в отношении дробей

— А легко ли теперь сравнить дроби из пункта в)?

— Как Вы назвали полученный нами способ сравнения?

— Проговорите ещё раз суть способа сравнения дробей дополнением до 1.

— А можно ли, используя способ дополнения до 1, сравнить дроби

— А может у кого-то из Вас есть гипотеза как это сделать или предположение, в каком направлении нам следует двигаться?

— Тогда я предлагаю Вам поработать в парах над следующим заданием, которое я надеюсь, поможет найти выход из этого затруднительного положения.

— У Вас на партах лежат рисунки, по которым Вам надо:

1. Записать изображённые на рисунках дроби.

2. Составить из них все возможные неравенства.

3. Результат работы представить на доске под соответствующим рисунком.

( Раздаются 4 вида карточек). (Приложение 1)

— Что общего Вы заметили в представленных сравнениях? (1/2).

— Проанализируйте их и сделайте вывод, с каким числом и как Вам приходилось сравнивать?

— А теперь проверьте верно, или неверно было выполнено Ваше сравнение последней пары дробей и объясните почему?

— Какое название данному способу сравнения Вы бы дали?

— Ещё раз сформулируйте суть способа сравнения дробей с ½.

— Более общее название этого способа – это сравнение дробей с промежуточным числом, которое может быть как дробным, так и целым, если мы имеем дело с неправильными дробями.

— Итак, какие новые способы сравнения обыкновенных дробей мы можем применять при решении задач на сравнение?

( Проговаривают названия, а учитель закрепляет их названия на сосуде.)

5. Первичное закрепление во внешней речи.

Выполняют задания карточки №1 «цепочкой» с проговариванием использованного способа сравнения.

КАРТОЧКА № 1 КАРТОЧКА № 1 (Ответы)

(Закрепление полученных знаний) (Закрепление полученных знаний0

Сравните дроби и определите 1.Сравните дроби и определите

способ сравнения: способ сравнения:

и › (по знаменателю)

и ‹ ( сравнение с ½)

и ‹ (сравнение с 1)

и ‹ (приведение к О.З.)

и › ( по числителю)

и ‹ (по дополн. до 1)

и ‹ ( приведение к О.Ч.)

и › (ср с промеж.чис.)

6. Самостоятельная работа с самопроверкой в классе ( 5 минут).

Выполняют задания карточки № 2.

(Самостоятельная работа с самопроверкой)

Сравните дроби наиболее «удобным»

Источник