Виды нестандартных задач, способы их решения

В данной презентации собраны основые виды нестандартных задач, изучаемых в начальной школе и рассмотрены способы их решения.
Просмотр содержимого документа
«Виды нестандартных задач, способы их решения»
Эффективное решение нестандартных творческих задач
для младших школьников
Знание только тогда знание, когда оно приобретено усилиями твоей мысли, а не памяти.
Развитие творческих способностей – важнейшая задача начального образования, ведь этот процесс пронизывает все этапы развития личности ребёнка, пробуждает инициативу и самостоятельность принимаемых решений, привычку к свободному самовыражению, уверенность в себе.
Творчество – это всегда новое, неизведанное, непредсказуемое, увлекательное и захватывающее.
Одним из средств развития интеллектуальных и творческих способностей младших школьников является решение нестандартных задач.
« Нестандартные задачи – это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения»,- писал Л.М.Фридман.
Нестандартная задача – это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способов решения, ни того, на какой учебный материал опирается решение.
Понятие «нестандартная задача» является относительным.
Одна и та же задача может быть стандартной или нестандартной, в зависимости от того, знакомы ли учащиеся со способами решения задач такого типа.
При решении занимательных задач преследуются следующие цели:
- формирование и развитие мыслительных операций: анализа, синтеза, сравнения, аналогии, обобщения и т.д.;
- развитие и тренинг мышления вообще и творческого в частности;
- поддержание интереса к предмету, к учебной деятельности;
- развитие качеств творческой личности (познавательная активность, упорство в достижении цели, самостоятельность, усидчивость);
- подготовка учащихся к творческой деятельности (творческое усвоение знаний, способов действий, умение переносить знания и способы действий в незнакомые ситуации и видеть новые функции объекта)
Помогая ученику, учитель должен оказать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика.
1.Старайся научить своих учеников догадываться.
2.Старайся научить своих учеников доказывать.
3.Пользуйся наводящими указаниями, но не старайся навязывать своего мнения насильно.
Нестандартные задачи по математике, используемые в начальной школе, условно можно разделить на следующие группы :
- задачи на взвешивание
- задачи на переливание;
- задачи, решаемые с «конца»;
- задачи на установление взаимно-однозначного соответствия между множествами;
- задачи о лжецах;
- задачи о переправах;
- задачи, решаемые с помощью логических выводов и т.д.
- алгебраический;
- арифметический;
- графический;
- практический;
- метод предположения;
- метод перебора
- способ рассуждений;
- способ составления таблиц;
- способ построения графов;
- способ бильярда;
- способ кругов Эйлера
Приёмы работы над задачей
1. Изучение условия задачи.
2. Выдвижение идеи(плана) задачи.
3. Поиск аналогии, сравнительные чертежи.
4. Разбиение задачи на подзадачи.
5. Решение одной задачи несколькими способами.
6. Приём разбора готового решения.
Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий :
1. Задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.
2. Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения.
3. Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.
- усвоить процесс решения любой задачи(читаю задачу, выделяю, что известно и что надо узнать);
- познакомиться с приемами работы над задачей(видами наглядной интерпретации, поиска решения, проверки решения задачи и др.)
На втором этапе учащиеся применяют ранее сформулированные общие приемы в ходе самостоятельного поиска решения конкретных задач.
При поиске решения незнакомой задачи полезно сделать чертеж (рисунок), т.к. именно он может быть способом решения задачи.
Если тебе трудно решить задачу, то попробуй:
— сделать к задаче рисунок или чертеж (подумай, может быть нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи);
— ввести вспомогательный элемент (часть);
— использовать для решения задачи способ подбора;
— переформулировать задачу другими словами, чтобы она стала более понятной и знакомой;
— разделить условие или вопрос задачи на части и решить ее по частям;
— начать решение задачи с «конца»
Задачи на взвешивание – достаточно распространенный вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний.
Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.
Из девяти монет одна фальшивая: она легче остальных.
Как за два взвешивания на чашечных весах без гирь определить, какая именно монета фальшивая?
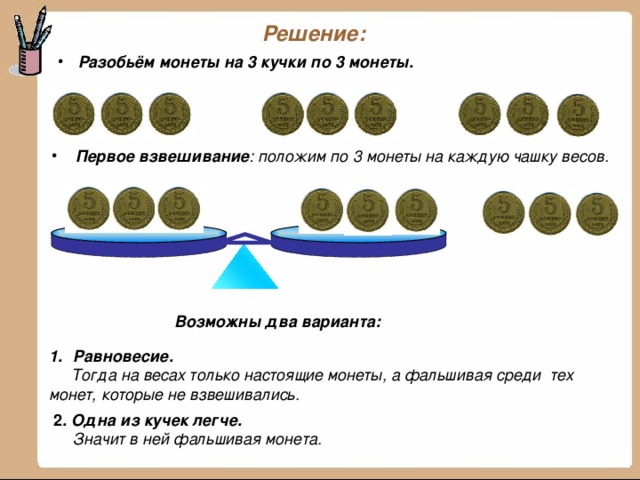
- Разобьём монеты на 3 кучки по 3 монеты.
- Первое взвешивание: положим по 3 монеты на каждую чашку весов.
Возможны два варианта:
Тогда на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались.
Значит в ней фальшивая монета.
- Второе взвешивание:теперь требуется найти фальшивую среди трёх монет ( по методу первого взвешивания).
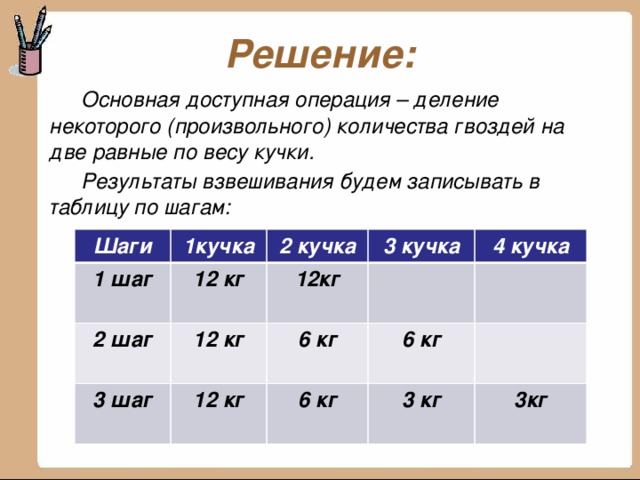
В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9 кг гвоздей?
Основная доступная операция – деление некоторого (произвольного) количества гвоздей на две равные по весу кучки.
Результаты взвешивания будем записывать в таблицу по шагам:
Источник
Зачетная работа на тему «Способы решения нестандартных задач»
«Способы решения нестандартных задач по математике»
Подготовила: учитель МБОУ «Лицей «МОК №2»г. Воронеж Павлова С.Н.
Глава 2. Способы решения нестандартных задач
2.1 Общие рекомендации по работе над нестандартной задачей…………
2.2 Нестандартные арифметические задачи и способы их решения………
2.3 Комбинаторные задачи и способы их решения…………………………
2.4 Логические задачи и способы их решения…………………………….
Важнейшим приоритетом начального общего образования в настоящее время является формирование общеучебных умений, навыков и способов познавательной деятельности, уровень освоения которых в значительной мере предопределяет успешность обучения на последующих этапах образования.
Согласно стандартам нового поколения, выпускник начальной школы должен владеть обобщёнными способами решения учебных задач, его необходимо научить осмысленно обрабатывать информацию, анализировать её, выявлять главное, «ядро» информации, устанавливать взаимосвязи между понятиями, проводить классификацию, сравнивать, делать обобщения. Это мыслительные операции, которые включает в себя словесно – логическое мышление. Этот тип мышления должен стать доминирующим к концу начальной школы.
Мышление человека, главным образом, состоит из постановки и решения задач. Особенно большую роль играют задачи в обучении математике. В них заложены большие возможности для повышения общего и математического образования учащихся, развития смекалки, начал исследовательской работы, логического мышления.
Поэтому, кроме системы типовых задач, решать которые обязан уметь каждый ученик, в обучении все чаще стали встречаться и такие задачи, которые не укладываются в эту систему. Их в методической литературе называют нестандартными /нетиповыми/.
Анализ опыта работы в школе показывает, что нестандартные задачи находят все более частое и широкое применение в обучении математике.
Учителя включают нестандартные арифметические задачи в уроки математики, предлагают для домашней самостоятельной работы, используют во внеклассной работе с учениками. Однако результативность такой работы иногда оказывается не столь высокой, как хотелось бы. При выполнении олимпиадных работ ученики не могут самостоятельно решить задачу, у них возникают трудности при оформлении решения.
Все вышеизложенное свидетельствует об актуальности темы работы.
Объект исследования: понятие нестандартной задачи.
Предмет исследования: способы решения нестандартных задач.
Гипотеза исследования: систематическое и целенаправленное использование различных способов решения нестандартных задач в процессе обучения математики в начальных классах способствует формированию умения самостоятельно и осознанно проводить поиски решения текстовых задач.
Цель: раскрытие особенностей различных способов решения нестандартных задач.
1) осуществить обзорный анализ психолого-методической литературы по исследуемой проблеме;
2) изучить методику работы над нестандартными задачами в начальных классах.
3) классифицировать нестандартные задачи и определить способы их решения.
ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ИЗУЧЕНИЯ
1.1 Понятие «нестандартная задача» и их виды
Какая задача по математике может называться нестандартной? Хорошее определение приведено в книге «Как научиться решать задачи» авторов Л.М. Фридмана, Е.Н. Турецкого.
«Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения» [13] . Не следует путать их с задачами повышенной сложности. Условия задач повышенной сложности таковы, что позволяют ученикам довольно легко выделить тот математический аппарат, который нужен для решения задачи по математике. Учитель контролирует процесс закрепления знаний, предусмотренных программой обучения решением задач этого типа. А вот нестандартная задача предполагает наличие исследовательского характера. Однако если решение задачи по математике для одного учащегося является нестандартным, поскольку он незнаком с методами решения задач данного вида, то для другого – решение задачи происходит стандартным образом, так как он уже решал такие задачи и не одну. Одна и та же задача по математике в 4 классе нестандартна, а в 5, 6 классах она является обычной, и даже не повышенной сложности.
Итак, если решение задачи учащийся не знает, на какой теоретический материал ему опираться, он тоже не знает, то в этом случае задачу по математике можно назвать нестандартной на данный период времени.
Традиционно нестандартными для младших школьников являются:
некоторые виды арифметических текстовых задач (задачи на предположение, на движение мимо объектов с учетом их протяженности, на движение в одном направлении; задачи, решаемые способом уравнивания или замены данных, методом инверсии (т. е. с «конца»); задачи с неопределенными неизвестными);
некоторые виды геометрических задач (деление фигур на части, составление фигуры из частей, преобразование фигур);
логические задачи (на установление временных, пространственных, функциональных отношений; на активный перебор вариантов; на планирование деятельности; на установление сходства и отношения между элементами множеств; на оперирование категориями все , некоторые , отдельные ); процессуальные задачи (задачи о переправах; задачи о переливаниях; задачи о взвешиваниях)
комбинаторные задачи (на упорядочение предметов; на выбор подмножеств и их упорядочение; на определение количества различных вариантов; на выбор наилучшего результата по определенным критериям).
К тому же воспитание интереса младших школьников к математике, развитие их математических способностей невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических фокусов, числовых головоломок, арифметических ребусов и лабиринтов.
Характер указанных задач, уровень их трудности и сложности определяются реальными возможностями и потребностями учебного процесса, возрастными особенностями обучаемых и их математической подготовкой.
1.2 Значение нестандартных задач в практике обучения математике
Нестандартная задача, как особый вид математических упражнений, является темой многих зарубежных и отечественных исследований. История вопроса уходит в глубину веков и восходит к «коллекциям проблем» египтян, греков, индийцев, китайцев, арабов.
В настоящее время исследованию процесса решения нестандартных задач посвящены работы психологов, педагогов, математиков (Д. Пойа, Л. М. Фридмана, Ю. М. Колягина и других), которые позволяют сделать вывод о том, что в процессе обучения решению задач развивается интеллект учащихся.
Решение задач имеет большое образовательное и воспитательное значение. Н. А. Мечинская и М. И. Моро отмечают, что решение задач всегда рассматривалось как такая учебная деятельность, которая преследует двоякую цель: во-первых, решение задач является средством, способствующим усвоению математических понятий и законов, а во-вторых, оно имеет самостоятельную ценность, поскольку служит для развития творческого мышления учащихся.
Внимание специалистов к нестандартным задачам определяется тем, что:
1. В их сюжетах находят отражение практические ситуации, знакомые ребенку, поэтому в рассуждениях он может опираться на свой жизненный опыт.
2. Задачи данной категории позволяют школьнику убедиться в прикладном характере математических методов, которыми он овладевает на уроках математики.
3. При их решении формируются общеучебные умения, необходимые для решения любой математической задачи, и навыки ориентировки в сложной ситуации, что позволяет считать нестандартные задачи мощным инструментом развития человеческого интеллекта.
4. Для решения нестандартных задач учащимся необходимо приложить определенные усилия, проявить волю, настойчивость, целеустремленность. Необычность приемов решения прививает вкус к самостоятельным исследованиям, к проявлению изобретательности, пробуждает положительные эмоции, как в процессе решения задач, так и при достижении результата.
Эффективно организованная учебная деятельность школьников в процессе решения указанных задач является важнейшим средством формирования математической культуры, таких качеств математического мышления, как гибкость, критичность, логичность, рациональность, органическое сочетание которых проявляется в особых способностях человека, дающих ему возможность успешно осуществлять творческую деятельность.
Значимость нестандартных задач определяется тем, что они обеспечивают:
1) усвоение программных знаний на более высоком уровне, так как процесс их решения не связан с необходимостью применения заученных правил и приемов, а требует мобилизации всех накопленных знаний, приучает к поиску своеобразных, нешаблонных способов действия;
2) возможность выявления математических и общеинтеллектуальных способностей учащихся, установления уровня обученности и обучаемости, развития математического мышления, формирования познавательных интересов;
3) проверку способности и умения самостоятельно учиться.
Присущие нестандартным задачам занимательность, яркость, необычность изложения и хода решения позволяют преобразовать любопытство на более высокую стадию развития, поскольку являются «пусковым механизмом» детской любознательности. Удивление учащихся может быть направлено на весь спектр приемов, возможных способов решения задач, на их многообразие. Так на основе формирования и развития интереса к решению задач данного типа можно поддержать возникший у школьников интерес к изучению учебного предмета, к учебной деятельности и к ее результатам.
1.3 Требования, предъявляемые к нестандартным задачам в начальной школе
Использованию в практике преподавания в начальной школе нестандартных математических задач предшествует большая подготовительная работа по их отбору. Поэтому необходимо сформулировать требования, на основе которых осуществляется отбор задач для начального математического образования. Критерии оценки качества задач школьного курса математики сформулированы Ю. М. Колягиным [7]. Конкретизируем их с учетом специфики учебного опыта и возрастных особенностей учащихся начальных классов.
1. Задача, предъявляемая младшему школьнику, должна быть интересной и значимой для ученика, должна вызвать его желание к исследованию за счет:
— элементов новизны или занимательности в фабуле задачи как благоприятного фактора возбуждения интереса учеников к математике и мотивирования их интеллектуального труда;
— реальности описываемой в задаче ситуации, ее близости жизненному опыту ребенка;
— неожиданного, оригинального решения, требующего применения известных методов в необычных условиях, рационализации и упрощения уже известного приема.
2. Задача должна соответствовать возможностям учащихся начальных классов. Младший школьник должен не только хотеть, но и быть в состоянии решить предложенную задачу. Разочарование учеников слишком трудными математическими вопросами является одной из причин торможения их развития. Нерешенная задача отрицательно влияет на воспитание интереса к математике. Поэтому очень важно, особенно на начальном этапе обучения предмету, чтобы поставленные перед школьниками нестандартные задачи были ими успешно решены. В этой связи внедренные в содержание начального математического образования нестандартные задачи должны:
а) соответствовать по объему элементов и сложности их отношений уровню теоретических знаний и практическому опыту учащихся (в целях обеспечения возможности самостоятельного их решения или хотя бы его понимания);
б) иметь преимущественно лаконичные формулировки;
в) допускать практическое решение (необходимым условием этого является наличие небольших числовых данных), а также разные варианты решения и способы проверки его правильности. В то же время решение задачи не должно быть слишком легким, основанным на догадках, не требующих ни знаний, ни навыков практических действий.
3. Система нестандартных задач для начальной школы должна включать в себя все основные темы курса, тем самым обеспечивая отработку необходимых, предусмотренных программой знаний и умений, т. е. быть полной . Кроме этого, структурные характеристики задачи должны быть разноплановы: с полным (или недостаточным) набором условий, с наличием избыточных данных. Это приучает учеников не доверять внешнему облику задачи и не приступать к ее решению сразу, полагая, что внешний вид совпадает с действительным содержанием.
Эффективность обучения младших школьников решению нестандартных задач зависит, на наш взгляд, от нескольких условий. Во-первых, задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся. Во-вторых, необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения. В-третьих, нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.
ГЛАВА 2. СПОСОБЫ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ
2.1 Общие рекомендации по работе над нестандартной задачей
Решение нестандартных задач есть искусство, которым можно владеть лишь в результате глубокого постоянного самоанализа действий по решению задач и постоянной тренировки в решении разнообразных задач.
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их», — советует Д. Пойа [9] . Главное при этом – сформировать такой общий подход к решению задач, когда задача рассматривается как объект для исследования, а ее решение – как конструирование и изобретение способа решения. Естественно, что такой подход требует не бездумного решения огромного числа задач, а неторопливого, внимательного и обстоятельного решения значительно меньшего числа задач, но с последующим анализом проведенного решения.
Итак, общих правил решения нестандартных задач нет (поэтому – то эти задачи и называются нестандартными). Однако выдающиеся математики и педагоги (С.А. Яновская, Л.М. Фридман, Э.Н. Балаян) нашли ряд общих указаний и рекомендаций, которыми можно руководствоваться при решении нестандартных задач:
а) вычленить из задачи или разбить ее на подзадачи стандартного вида (способ разбиения), привлечь аналогию;
б) ввести в условие вспомогательные элементы, построения;
в) заменить задачу другой равносильной задачей (способ моделирования).
Для сведения нестандартной задачи к стандартной не существует определенных правил. Однако если внимательно, вдумчиво анализировать, решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами были решены задачи, то вырабатывается умение в таком сведении.
Конечно, может встретиться задача, к которой не удастся применить ни одного из перечисленных правил. Тогда нужно изобрести особый метод решения этой задачи.
Деятельность по решению текстовых математических задач, в том числе и нестандартных, включает следующие этапы:
1) анализ текста задачи (усвоение содержания);
2) поиск решения (разбор задачи и составление плана решения);
3) осуществление плана решения;
4) проверка решения задачи.
Установлено, что основные затруднения при решении задач данного вида возникают у учащихся прежде всего на начальных этапах хода решения, так как их попытки выбрать теоретический базис и способ действия, полагаясь на имеющийся субъектный опыт, в рассматриваемой ситуации не всегда успешны. Поэтому на этапе анализа текста задачи можно рекомендовать:
интерпретировать условие задачи, т. е. выполнить рисунок, чертеж, таблицу, схему для получения ясного представления о задачной ситуации;
выделить данные и искомые, отношения между ними, проверить их достаточность и непротиворечивость;
обратиться к прошлому опыту: вспомнить аналогичные, уже решенные задачи, на которые данная задача может опираться;
перевести элементы задачи на язык математического метода, предполагаемого для использования при ее решении;
переформулировать условие задачи, заменив данное в ней описание ситуации другим, сохраняющим все отношения, связи, количественные характеристики объектов задачи (при этом вся лишняя, несущественная информация отбрасывается, текст задачи преобразуется в форму, сокращающую поиск решения).
При поиске решения задачи уместно попытаться свести ее к ранее решенным; отбросить несущественную, излишнюю информацию, заменить описание некоторых понятий соответствующими терминами, переорганизовать текст задачи в форму, удобную для поиска решения; расчленить задачу на серию вспомогательных задач, последовательное решение которых составит решение данной задачи.
На этапе осуществления плана решения задачи ученику полезно придерживаться советов, касающихся выбора способа оформления решения, гарантирующего фиксацию рассуждений в краткой и ясной, но достаточной для полного воспроизведения решения форме, а также проводить коррекцию правильности решения путем сравнения с условием.
Закончив решение задачи, следует осуществить его проверку : прикинуть правильность результата сопоставлением с условием и здравым смыслом; установить соответствие между данными и искомыми; попытаться найти более экономичный способ решения; составить и решить обратную задачу.
Метод указаний позволяет детям успешнее и быстрее решить задачу, но применять его нужно только тогда, когда есть полная уверенность в его полезности. Если задача такова, что в ходе ее решения предстоит сделать слишком много указаний, то полезнее применить прием разбора готового решения.
В процессе решения очень трудных задач нестандартного характера следует уделять особое внимание актуализации знаний учащихся. Полезно использовать специально подобранные серии задач, составленные, с учетом прошлого опыта решающих. Для облегчения решения задачи надо построить систему задач так, чтобы при решении сложных можно было использовать ранее решенные задачи. Данный дидактический прием назван системой подсказок. Он делает поиск решения целенаправленным, создает оптимальные условия для активизации мыслительной деятельности учащихся, способствует развитию умения нешаблонно, с интересом подойти к решению задачи, систематизирует знания и субъектный опыт.
Метод решения одной задачи несколькими способами. Зачем он? Различные способы решения задачи дают возможность использовать те или иные теоретические положения. Это делает знания более прочными, осознанными.
2.2 Нестандартные арифметические задачи и способы их решения
Как показала школьная практика, обучение младших школьников решению нестандартных арифметических задач можно разделить на два этапа. На первом этапе проводится специальная работа по выводу и осмыслению общих подходов к решению таких задач. При этом важно, чтобы ученики уже усвоили процесс решения любой арифметической задачи (читаю задачу; выделяю, что известно и что надо узнать, и т.д.); познакомились с приемами работы на каждом этапе решения задачи (виды наглядной интерпретации, поиска решения, проверки решения задачи и др.). На втором этапе учащиеся применяют ранее сформулированные общие приемы в ходе самостоятельного поиска решения конкретных задач.
Опишем, как можно провести работу на первом этапе.
1. Для того чтобы решить задачу, бывает полезно построить к ней рисунок или чертеж. Следует начинать с этой рекомендации, так как ученики уже делали такой вывод при решении стандартных задач. Но в данном случае должны быть выделены некоторые особенности использования графических изображений. Во-первых, ответ, а в некоторых случаях часть неизвестных могут быть получены только из чертежа без выполнения арифметических действий. Во-вторых, иногда нужно будет делать дополнительные построения, т.е. в процессе решения задачи будут выполнены новые чертежи с учетом найденных чисел. Чертеж будет использоваться также и при применении других приемов нестандартных задач.
Задача 1. Бревно длиной 12 м распилили на 6 равных частей. Сколько распилов сделали?
После чтения задачи ученикам предлагается ответить на вопрос, решали ли они задачи такого вида и известен ли им способ решения таких задач.
Возможно, некоторые ученики ошибочно будут считать, что знают, как решить задачу: «Надо 12 м разделить на 6 равных частей». Учитель должен дать учащимся возможность найти результат, оценить его и убедиться в ошибке. (Разделив 12 на 6, мы узнали, что длина одной части равна 2 м. Но в задаче спрашивается, не какова длина одной части, а сколько сделали распилов. Следовательно, задача решена неправильно.) Затем ученики могут вновь прийти к ошибочному заключению: «Сколько частей, столько и распилов». Учитель предлагает проверить найденный ответ, сделав условный рисунок или чертеж. Ученики обозначают бревно прямоугольником или отрезком длиной 12 клеточек, делят его вертикальными засечками на 6 равных частей. Подсчитав число полученных засечек (распилов), они убеждаются, что их 5, а не 6, как они считали раньше. Эту задачу решили, не выполняя арифметических действий. Ответ получили, построив чертеж (рисунок). Под ним ученики записывают ответ задачи. Таким образом, учащиеся приходят к следующему выводу: при поиске решения незнакомой задачи полезно сделать чертеж (рисунок), так как работа с чертежом (рисунком) может являться способом решения задачи.
2. При решении нестандартных задач в некоторых случаях часть данных целесообразно найти с помощью графических изображений (рисунков, чертежей), а часть — с помощью арифметических действий.
Задача 2. Ширина занавески для окна равна 1 м 20 см. Надо пришить 6 колец на одинаковом расстоянии друг от друга (первое и последнее кольца должны располагаться по краям занавески). Сколько сантиметров надо оставлять между кольцами?
Следуя ранее выведенной рекомендации, ученики начинают делать схематический чертеж к данной задаче. Они показывают засечкой первое кольцо, откладывают отрезок любой выбранной длины, ставят вторую засечку, откладывают отрезок такой же длины, как первый, ставят третью засечку и так действуют до тех пор, пока не поставят 6 засечек. По полученному схематическому чертежу подсчитывают число равных частей, на которые 6 колец разделят занавеску.
Для того чтобы ответить на вопрос задачи, остается разделить всю ширину занавески на 5 равных частей: 120 : 5 = 24 (см).
3. Иногда в процессе решения задачи нужно делать дополнительные построения или перестраивать чертежи с учетом найденных чисел. Это можно сделать при решении следующей задачи.
Задача 3. Муравей находится на дне колодца глубиной 30 м. За день он поднимается на 18 м, а за ночь сползает вниз на 12 м. Сколько дней нужно муравью, чтобы выбраться из колодца?
Самостоятельно решая эту задачу, учащиеся могут сделать чертеж (рис.1) и неверно решить задачу:
1) 18 — 12 = 6 (м) — поднимается муравей за сутки.
2) 30 : 6 = 5 (сут.) — потребуется муравью, чтобы выбраться из колодца.
Учитель предлагает: а) проверить решение, показав на отдельных чертежах положение муравья в каждый день; б) в ходе решения подсчитывать, сколько метров остается муравью, чтобы выбраться из колодца.
Таким образом, ученики видят, что в третий день муравей поднимется на 18 м и выберется из колодца. Значит, сначала они решили задачу неправильно. А найти верный ответ им помогло последовательное построение нескольких чертежей, отражающих те изменения, которые происходили в реальной ситуации, описываемой в задаче.
4. Для того чтобы решить задачу, бывает нужно ввести вспомогательный элемент (часть).
Задача 4. Разложи 45 шариков в 4 коробки так, что если число шариков в третьей коробке увеличить в 2 раза, а в четвертой уменьшить в 2 раза, а в первой и второй оставить без изменения, то в каждой коробке будет одинаковое число шариков.
Сначала учащиеся выполняют первый схематический чертеж (рис. 3).
Анализируя чертеж, ученики замечают, что на нем есть отрезки одинаковой длины, но не все. Учитель предлагает дорисовать чертеж, чтобы все отрезки состояли из одинаковых частей (рис. 4).
Затем сообщает, что в таких случаях можно ввести вспомогательный элемент — часть. Примем число шариков в третьей коробке за 1 часть, тогда число шариков в четвертой коробке составит 4 части, в первой — 2 части, во второй — 2 части. Затем выполняется арифметическое решение:
1)2 + 2+1+4 = 9 (ч.) — составляют 45 шариков.
2) 45 : 9 = 5 (ш.) — содержится в 1 части или число шариков в третьей коробке.
3) 5 2 = 20 (ш.) — число шариков в первой или во второй коробке.
4) 5 4 = 20 (ш.) — число шариков в четвертой коробке.
В процессе поиска решения данной задачи использовали несколько приемов: строили и достраивали чертеж, вводили вспомогательный элемент. Его удобно ввести, когда на чертеже получены отрезки одинаковой длины.
5. При решении нестандартных задач: в поиске ответа на вопрос задачи можно использовать способ подбора.
Задача 5. Сумма четырех различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найди эти числа.
Сначала ученики выполняют чертеж (рис. 5).
Затем учащиеся пытаются преобразовать чертеж, чтобы получить одинаковые числа, как они делали в предыдущих задачах. Ученики приходят к выводу, что этого сделать нельзя, так как в условии ничего не говорится о числовых отношениях между вторым и третьим числом. Встает проблема: можно ли решить эту задачу? Может быть, в ней не хватает данных? Учитель предлагает использовать для решения этой задачи способ подбора.
Рассуждения удобнее начать с наименьшего из чисел.
Пробуем число 0. Тогда получаем: 0+ ? + ? + 5 = 13. Подберем пропущенные числа. Их сумма равна 13 — 5 — 0 = 8. Эти числа должны быть разными и быть больше 0, но меньше 5. Между 0 и 5 идут числа 1, 2, 3, 4. Среди них нельзя выбрать два разных числа, дающих в сумме 8. Значит, число 0 не подходит.
Пробуем число 1. Тогда получаем: l + ?+ ?+ 6 = 13. Подбираем пропущенные числа. Их сумма равна: 13-1-6 = 6. Между числами 1 и 6 стоят числа 2, 3, 4, 5. Среди них выбираем два, дающих в сумме 6. Это числа 2 и 4. Проверяем, правильно ли мы нашли четыре числа. Для этого складываем их: 1 + 2 + 4 + 6 = 13. Получили сумму, данную в задаче. Другие условия также соблюдены: числа различные, наименьшее из этих чисел 1, оно на 5 меньше наибольшего числа 6.
Получив один ответ, нужно проверить, нет ли других вариантов ответа. Для этого пробуем число 2. Тогда получаем: 2 + ? + ? + 7 = 13. Подбираем пропущенные числа. Их сумма равна 4. Среди чисел 3, 4, 5, 6 нельзя выбрать два числа, дающих в сумме 4 (сумма любых двух перечисленных чисел больше 4). Можно проверить число 3 таким же образом. Числа, начиная с 4, проверять не нужно, так как сумма двух чисел получается равной или больше: 13 : 4 + ? + ? + 9 = 13.
Получаем ответ задачи: числа 1, 2, 4, 6.
В итоге важно подчеркнуть, что задачу решили, подбирая нужные числа. Делали это так: последовательно рассматривали различные возможные варианты и выбрали те, которые соответствуют всем условиям задачи. Чертеж помогал выделить эти условия из текста задачи. В некоторых случаях перебор удобно начинать не с наименьшего, а с наибольшего возможного числа. Иногда, оценив полученный результат, можно пропустить некоторые числа. Этот способ удобно использовать, когда число возможных вариантов небольшое.
6. При решении нестандартных задач: полезно переформулировать задачу, т.е. сказать ее другими словами, чтобы она стала знакомой и понятной. При этом в большинстве случаев будет происходить перевод текста задачи на язык математики.
Задача 6. Число яблок в корзине двузначное. Эти яблоки можно раздать поровну 2, 3 или 5 детям, но нельзя раздать поровну 4 детям. Сколько яблок в корзине? (Укажите такое наименьшее двузначное число.)
Сначала ученики пытаются сделать рисунок или чертеж к задаче, но испытывают затруднения, так как на чертеже трудно показать, что нельзя раздать яблоки поровну 4 детям, следовательно, непонятно, как использовать чертеж для решения задачи. Тогда ученики начинают применять способ подбора. Учитель предлагает сначала изменить формулировку задачи, чтобы легче было выполнить перебор. Выясняется, что если яблоки можно раздать поровну 2, 3 и 5 детям, значит, число яблок делится на 2, 3. 5. Если яблоки нельзя раздать 4 детям поровну, значит, число яблок не делится на 4. Задачу переформулируют следующим образом: «Найди наименьшее двузначное число, которое делится на 2, 3,5 и не делится на 4».
Далее выполняется перебор. Ученики проверяют наименьшее двузначное число 10. Оно делится на 2 и 5, но не делится на 3, значит, число 10 не подходит. Перебор можно сократить, не рассматривать все числа подряд, а проверять только числа, делящиеся на 5. Число 15 не подходит, так как не делится на 2. Так ученики доходят до числа 30, которое делится на 2, 3, 5 и не делится на 4. Значит, в корзине 30 яблок.
Данную задачу можно было бы решить, выполняя чертеж. Начертить в тетради луч и откладывать на нем последовательно отрезки длиной 2, 3, 5 клеточек, найти точку, в которой соединяются концы отрезков трех видов, подсчитать число клеток от начала луча до этой точки. На чертеже следовало бы проверить, что отрезки длиной 4 клеточки не укладываются целое число раз в большом отрезке длиной 30 клеток. И только тогда назвать ответ задачи. Этот способ трудоемкий, но он может оказаться более легким для некоторых учеников в силу их индивидуальных особенностей.
7. При решении нестандартных задач: условие или вопрос задачи можно разделить на части и решить задачу по частям.
Задача 7. В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах стало пассажиров поровну. Сколько пассажиров было в каждом автобусе сначала?
По усвоенной первой рекомендации ученики вначале делают к задаче чертеж (рис. 6).
Учитель предлагает решать эту задачу, разбив ее на части, чтобы облегчить решение. Ученики читают первые три предложения из текста задачи и думают, что по этим данным можно узнать.
1) 8 — 3 = 5 (чел.) — поехали на машине.
2) 123 — 5 = 118 (чел.) — остались в каждом автобусе.
Затем решают задачу дальше:
3) 118 : 2 = 59 (чел.) — стало в каждом автобусе.
Чтобы легче было сформулировать последнюю часть задачи, можно переделать чертеж с учетом найденных данных. Ученики формулируют: «Из одного автобуса вышли 8 человек, и в нем осталось 59 человек. В другой автобус сели 3 человека, и в нем стало 59 человек. Сколько человек было в каждом автобусе сначала?» — и заканчивают решение:
4) 59 + 8 = 67 (чел.) — было в первом автобусе.
5) 59 — 3 = 56 (чел.) — было во втором автобусе.
Иногда полезно разделить на части не условие, а вопрос задачи. Так можно поступить при решении следующей задачи.
Задача 8. 18 ручек стоят на 30 рублей больше, чем 30 карандашей. Те же 18 ручек стоят на 10 рублей больше, чем 40 таких же карандашей. Сколько стоят 1 карандаш и 1 ручка?
Сначала ученики выполняют к задаче чертеж (рис. 7).
Затем, используя чертеж, отвечают сначала на первый вопрос: «Сколько стоит 1 карандаш?»
1) 40 — 30 = 10 (шт.) — разница в количестве карандашей.
2) 30 — 10 = 20 (р.) — стоят 10 карандашей.
3) 20 : 10 = 2 (р.) — стоит 1 карандаш.
После этого можно ответить на второй вопрос: «Сколько стоит 1 ручка?»
4) 2 30 = 60 (р.) — стоят 30 карандашей.
5) 60 + 30 = 90 (р.) — стоят 18 ручек.
6) 90 : 18 = 5 (р.) — стоит 1 ручка.
Данный прием используется в задачах с большим числом разных объектов или действий с ними, с несколькими вопросами.
8. При решении нестандартных задач: решать задачу можно, начиная «с конца».
Задача 9 . Мама дала детям конфеты: дочери половину всех конфет и ещё одну, сыну половину остатка и оставшиеся 5 конфет. Сколько всего конфет мама дала детям?
Ученики выполняют чертеж (рис. 8).
1) 5 2 + 1 = 11 (к.) — половина всех конфет
2) 11 2 = 22 (к.) – мама дала детям
Учитель предлагает начать решать задачу «с конца», так как известно, сколько конфет осталось в конце.
Совершая обратную операцию, учащиеся находят ответ.
Делается вывод о том, что, решая «с конца», последовательно пришли к тому, что было в самом начале. Прием используется, когда в задаче известно число, полученное в конце выполнения каких-либо действий.
Если тебе трудно решить задачу, то попробуй:
1) сделать к задаче рисунок или чертеж; подумай, может быть, нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи;
2) ввести вспомогательный элемент (часть);
3) использовать для решения задачи способ подбора;
4) переформулировать задачу другими словами, чтобы она стала более понятной и знакомой;
5) разделить условие или вопрос задачи на части и решить ее по частям;
6) начать решение задачи «с конца».
Важно объяснить детям, что данные указания носят рекомендательный характер. Необязательно применять их в той последовательности, как они записаны в памятке, необязательно выполнять все рекомендации при решении одной задачи, можно комбинировать их в разных сочетаниях. В этом суть творческого процесса решения нестандартных задач.
2.3 Комбинаторные задачи и способы их решения
Комбинаторная задача – это задача, решение которой предполагает перебор всех возможных вариантов решения или подсчет их количества.
Способы решения комбинаторных задач делятся на две группы:
Неформальный способ решения на первый план выводит сам процесс составления различных комбинаторных конфигураций. И главная его задача – быстро и правильно найти все возможные варианты.
К неформальным способам решения комбинаторных задач относят полный (непосредственный, хаотичный) перебор. Это самый элементарный способ, так как он не требует знания определений и формул. Поэтому именно его целесообразно использовать в начальной школе.
Сущность данного способа – перебрать, пересмотреть все возможные варианты и показать, что других быть не может. При этом важно, как организован процесс перебора, так как, если действовать случайным, хаотичным образом, то нельзя быть уверенным, что найдены все возможные комбинации. Чтобы избежать этого, нужно выполнять перебор по определенной системе, т.е. систематический перебор . Для этого используют комбинаторные таблицы, графы, «дерево решений».
По определению Н.Я. Виленкина, граф — это «множество, состоящее из конечного числа точек, некоторые пары которых соединены дугами (такие графы называются неориентированными; если вместо дуг используются стрелки, то получится ориентированный граф, или, орграф)».
A.M. Пышкало, Л.П.Стойлова, В.В.Рожденственская графом называют «особый чертеж, состоящий из точек и линий, идущих из одной точки в другую».
Задача 10: На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Решение: Вершины графа — это деревья, обозначенные первой буквой названия дерева. В данной задаче два отношения: ― «быть ниже» и ― «быть выше». Рассмотрим отношение ― «быть ниже» и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

Ответ: клен, яблоня, лиственница, рябина, сосна, дуб, береза, тополь.
Задача 11: В парке 5 беседок. Было решено от каждой беседки ко всем остальным проложить дорожку. Продолжи рисунок, покажи, какие дорожки будут сделаны. Посчитай, сколько всего будет дорожек.
Вершины графа — это беседки, обозначенные треугольниками (рис. 10).
Рассмотрим отношение между каждой беседкой. В задаче сказано, что нужно провести дорожки к каждой беседке. Продолжаем рисунок, проведя дорожки. Получаем граф, на котором видно сколько дорожек нужно провести.
Решение комбинаторных задач можно выполнить и с помощью таблиц. Они схожи с деревом возможных вариантов, поскольку предлагают наглядное решение ситуации. Для нахождения правильного ответа нужно сформировать таблицу, причем она будет зеркальной: горизонтальные и вертикальные условия будут одинаковыми. Возможные варианты ответов будут получаться на пересечении столбцов и строчек. При этом ответы на пересечении столбца и строки с одинаковыми данными получаться не будут, эти пересечения необходимо особо пометить, чтобы не запутаться при составлении итогового ответа.
Задача 12: Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.
Источник