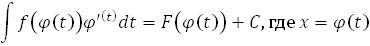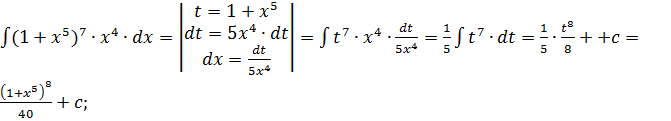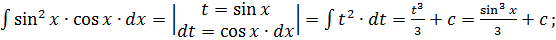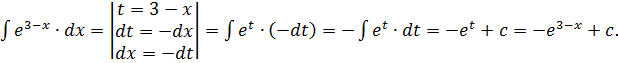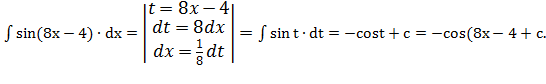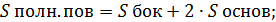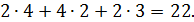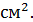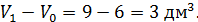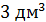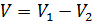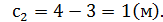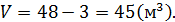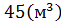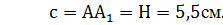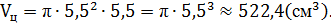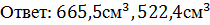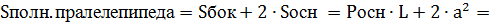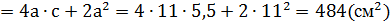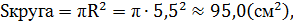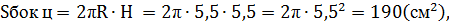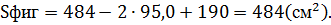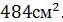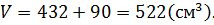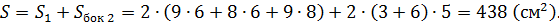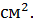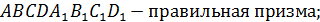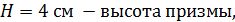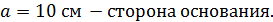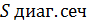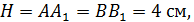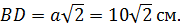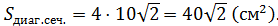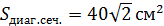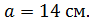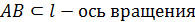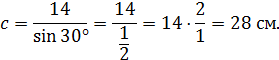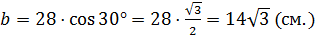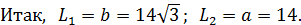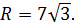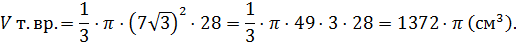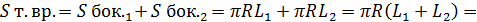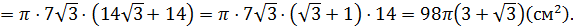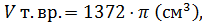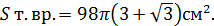Методы интегрирования
Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.
В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.
Метод непосредственного интегрирования
Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.
Вычислите множество первообразных функции f ( x ) = 2 x + 3 2 · 5 x + 4 3 .
Решение
Для начала изменим вид функции на f ( x ) = 2 x + 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 .
Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:
∫ f ( x ) d x = ∫ 3 2 · 5 x + 4 3 = 2 x + 3 2 · 5 x + 4 1 3 d x = ∫ 3 2 · 5 x + 4 1 3 d x
Выводим за знак интеграла числовой коэффициент:
∫ f ( x ) d x = ∫ 2 x d x + ∫ 3 2 ( 5 x + 4 ) 1 3 d x = = ∫ 2 x d x + 2 3 · ∫ ( 5 x + 4 ) 1 3 d x
Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫ 2 x d x = 2 x ln 2 + C 1
Чтобы найти второй интеграл, потребуется таблица первообразных для степенной функции ∫ x p · d x = x p + 1 p + 1 + C , а также правило ∫ f k · x + b d x = 1 k · F ( k · x + b ) + C .
Следовательно, ∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
У нас получилось следующее:
∫ f ( x ) d x = ∫ 2 x d x + 3 2 · ∫ 5 x + 4 1 3 d x = = 2 x ln 2 + C 1 + 3 2 · 3 20 · ( 5 x + 4 ) 4 3 + C 2 = = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
причем C = C 1 + 3 2 C 2
Ответ: ∫ f ( x ) d x = 2 x ln 2 + 9 40 · 5 x + 4 4 3 + C
Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.
Метод подстановки
Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.
Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.
Вычислите неопределенный интеграл ∫ 1 x 2 x — 9 d x .
Решение
Добавим еще одну переменную z = 2 x — 9 . Теперь нам нужно выразить x через z :
z 2 = 2 x — 9 ⇒ x = z 2 + 9 2 ⇒ d x = d z 2 + 9 2 = z 2 + 9 2 ‘ d z = 1 2 ·2 z d z = z d z
Далее подставляем полученные выражения в исходный интеграл и получаем:
∫ d x x 2 x — 9 = ∫ z d z z 2 + 9 2 · z = 2 ∫ d z z 2 + 9
Берем таблицу первообразных и узнаем, что 2 ∫ d z z 2 + 9 = 2 3 a r c t g z 3 + C .
Теперь нам нужно вернуться к переменной x и получить ответ:
2 3 a r c t g z 3 + C = 2 3 a r c t g 2 x — 9 3 + C
Ответ: ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .
Если нам приходится интегрировать функции с иррациональностью вида x m ( a + b x n ) p , где значения m , n , p являются рациональными числами, то важно правильно составить выражение для введения новой переменной. Подробнее об этом читайте в статье, посвященной интегрированию иррациональных функций.
Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.
Этот метод объясняет правило интегрирования ∫ f ( k · x + b ) d x = 1 k · F ( k · x + b ) + C .
Добавляем еще одну переменную z = k · x + b . У нас получается следующее:
x = z k — b k ⇒ d x = d z k — b k = z k — b k ‘ d z = d z k
Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:
∫ f ( k · x + b ) d x = ∫ f ( z ) · d z k = 1 k · ∫ f ( z ) d z = = 1 k · F z + C 1 = F ( z ) k + C 1 k
Если же мы примем C 1 k = C и вернемся к исходной переменной x , то у нас получится:
F ( z ) k + C 1 k = 1 k · F k x + b + C
Метод подведения под знак дифференциала
Это метод основывается на преобразовании подынтегрального выражения в функцию вида f ( g ( x ) ) d ( g ( x ) ) . После этого мы выполняем подстановку, вводя новую переменную z = g ( x ) , находим для нее первообразную и возвращаемся к исходной переменной.
∫ f ( g ( x ) ) d ( g ( x ) ) = g ( x ) = z = ∫ f ( z ) d ( z ) = = F ( z ) + C = z = g ( x ) = F ( g ( x ) ) + C
Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.
Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.
Вычислите неопределенный интеграл ∫ c t g x d x .
Решение
Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.
c t g x d x = cos s d x sin x
Смотрим в таблицу производных и видим, что числитель можно подвести под знак дифференциала cos x · d x = d ( sin x ) , значит:
c t g x d x = cos x d x sin x = d sin x sin x , т.е. ∫ c t g x d x = ∫ d sin x sin x .
Допустим, что sin x = z , в таком случае ∫ d sin x sin x = ∫ d z z . Согласно таблице первообразных, ∫ d z z = ln z + C . Теперь вернемся к исходной переменной ∫ d z z = ln z + C = ln sin x + C .
Все решение в кратком виде можно записать так:
∫ с t g x d x = ∫ cos x d x sin x = ∫ d sin x sin x = s i n x = t = = ∫ d t t = ln t + C = t = sin x = ln sin x + C
Ответ: ∫ с t g x d x = ln sin x + C
Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.
Метод интегрирования по частям
Этот метод основывается на преобразовании подынтегрального выражения в произведение вида f ( x ) d x = u ( x ) · v ‘ x d x = u ( x ) · d ( v ( x ) ) , после чего применяется формула ∫ u ( x ) · d ( v ( x ) ) = u ( x ) · v ( x ) — ∫ v ( x ) · d u ( x ) . Это очень удобный и распространенный метод решения. Иногда частичное интегрирование в одной задаче приходится применять несколько раз до получения нужного результата.
Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.
Вычислите неопределенный интеграл ∫ a r c t g ( 2 x ) d x .
Решение
Допустим, что u ( x ) = a r c t g ( 2 x ) , d ( v ( x ) ) = d x , в таком случае:
d ( u ( x ) ) = u ‘ ( x ) d x = a r c t g ( 2 x ) ‘ d x = 2 d x 1 + 4 x 2 v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x
Когда мы вычисляем значение функции v ( x ) , прибавлять постоянную произвольную С не следует.
Далее используем формулу интегрирования по частям и получаем:
∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2
Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.
Поскольку ∫ a r c t g ( 2 x ) d x = u ( x ) · v ( x ) — ∫ v ( x ) d ( u ( x ) ) = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 , тогда 2 x d x = 1 4 d ( 1 + 4 x 2 ) .
∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — ∫ 2 x d x 1 + 4 x 2 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C 1 = = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C
Ответ: ∫ a r c t g ( 2 x ) d x = x · a r c t g ( 2 x ) — 1 4 ln 1 + 4 x 2 + C .
Главная сложность применения такого метода – это необходимость выбирать, какую часть брать за дифференциал, а какую – за функцию u ( x ) . В статье, посвященной методу интегрирования по частям, даны некоторые советы по этому вопросу, с которыми следует ознакомиться.
Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.
Если мы интегрируем степенное выражение вида sin 7 x · d x или d x ( x 2 + a 2 ) 8 , то нам будут полезны рекуррентные формулы, которые могут постепенно понижать степень. Они выводятся с помощью последовательного многократного интегрирования по частям. Советуем прочитать статью «Интегрирование с помощью рекуррентных формул.
Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.
Источник
Метод подстановки в неопределенном интеграле
Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда, а иногда это связано с большими трудностями. В этих случаях применяют другие приемы. Одним из наиболее эффективных приемов является метод подстановки или замены переменной интегрирования. Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный интеграл к новому интегралу, который сравнительно легко берется непосредственно. Если после замены переменной интеграл стал проще, то цель подстановки достигнута. В основе интегрирования методом подстановки лежит формула
Алгоритм вычисления неопределенного интеграла методом подстановки:
1. Определяют, к какому табличному интегралу приводится данный интеграл (предварительно преобразовав подынтегральное выражение, если нужно).
2. Определяют, какую часть подынтегральной функции заменить новой переменной, и записывают эту замену.
3. Находят дифференциалы обеих частей записи и выражают дифференциал старой переменной (или выражение, содержащее этот дифференциал) через дифференциал новой переменной.
4. Производят замену под интегралом.
5. Находят полученный интеграл.
6. В результате производят обратную замену, т.е. переходят к старой переменной.
7. Результат полезно проверять дифференцированием.
Задание:Найти неопределённые интегралы
1. 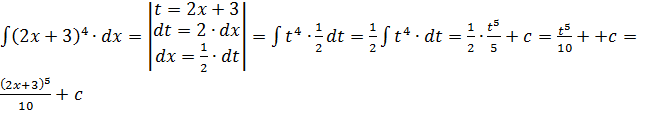
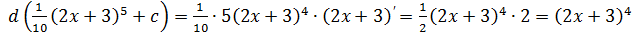
2.
3.
4.Предварительно преобразуем подынтегральную функцию в сложную степенную функцию, а затем применим метод подстановки в неопределённом интеграле:
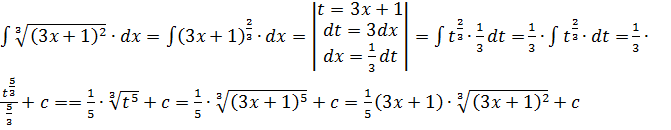
5.
6.
Наибольшую трудность при практическом применении метода подстановки вызывает правильность определения, к какому табличному интегралу удастся привести заданный интеграл.
Рассмотрим типовые варианты. В Таблице 1 приведены варианты правильных подстановок в различных типах неопределенных интегралов и те интегралы, к которым удаётся прийти в результате подстановки.
Таблица 1
| № п/п | Интеграл | Табличный интеграл, к которому будет приведен данный интеграл | Замена переменной |
| 1. | 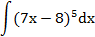 | 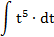 | t = 7x-8 |
| 2. | 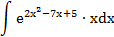 | 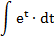 | t = 2x 2 -7x+5 |
| 3. | 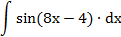 | 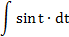 | t = 8x-4 |
| 4. | 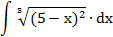 | 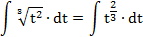 | t = 5-x |
| 5. | 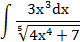 | 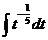 | t = 4x 4 +7 |
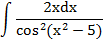 | 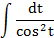 | t = x 2 -5 | |
| 7. | 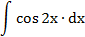 | 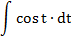 | t = 2x |
| 8. | 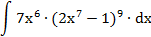 | 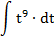 | t = 2x 7 -1 |
Методические указания и примеры типового расчёта
Практической работы №11 по теме
«Геометрические тела. Вычисление объёмов и площадей поверхности многогранников и тел вращения»
Теория
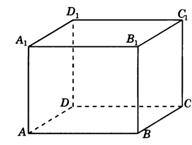
Параллелепипедом называется призма, в основании которой лежит параллелограмм.
1) Прямой 
2) Прямоугольный параллелепипед 
3) Куб 
Диагональное сечение призмы 
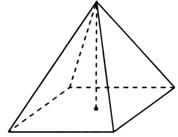
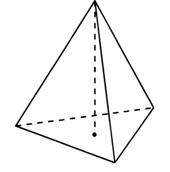
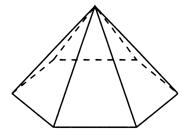
Пирамидой называется многогранник, в основании которого лежит произвольный многоугольник, а остальные грани являются треугольниками с общей вершиной.
1)Треугольная, четырёхугольная, пятиугольная. -в зависимости от многоугольника. лежащего в основании пирамиды;
2) Правильная и неправильная пирамида.
Пирамида называется правильной, если в её основании лежит правильный многоугольник и вершина пирамиды проектируется в центр основания.
Апофемой называется высота боковой грани правильной пирамиды, опущенная из её вершины (
Основные формулы
Куб: 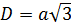
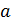
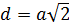
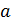
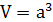
Призма: 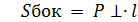
где 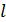
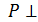
Sполн. призм. = Sбок + 2 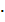
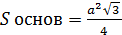
Vпризмы = Sоснов ·H, где Н- высота призмы, если призма прямая, то её высотой является боковое ребро ;
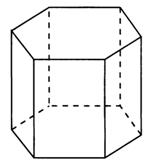
Пирамида:
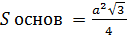
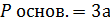
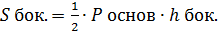
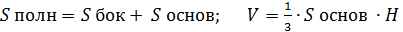
Усечённая пирамида:
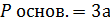
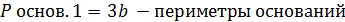
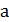
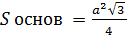
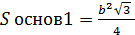
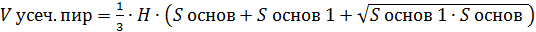
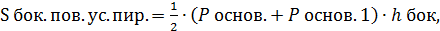
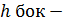
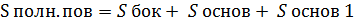
Тела вращения
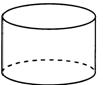
Цилиндр:
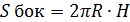
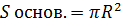
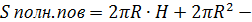
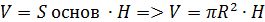
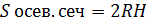
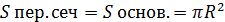
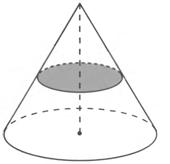
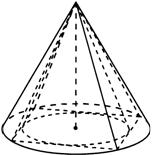
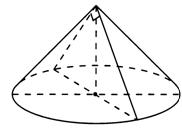
Конус:
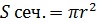
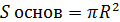
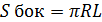
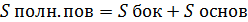
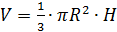
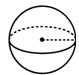
Шар:
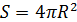
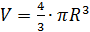
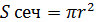
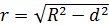
Вписанные и описанные многогранники и тела вращения:
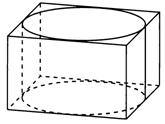
Рис.1 — Правильная четырёхугольная призма, описанная вокруг цилиндра;
Рис.2- Конус, описанный вокруг правильной четырёхугольной пирамиды, в которую вписан второй конус;
Рис.3- Прямоугольный параллелепипед, описанный вокруг сферы;
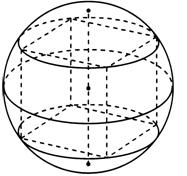
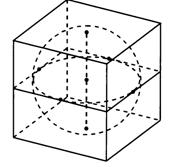
Рис.4- Куб, вписанный в шар;
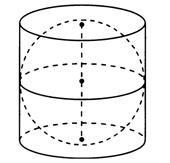
Рис.5- Цилиндр, описанный вокруг шара
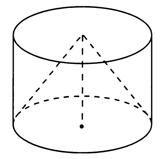
Рис.6-Конус, вписанный в цилиндр.
Задание 1. Найдите площадь многогранника, изображённого на рисунке. Все двугранные углы многогранника прямые.
Решение
Поверхность многогранника состоит из двух квадратов со стороной 2, площадь каждого из которых равна 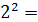
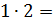
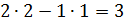
Ответ: 22
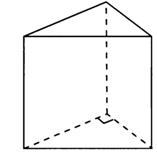
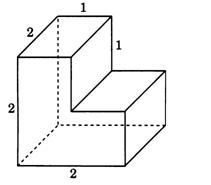
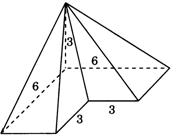
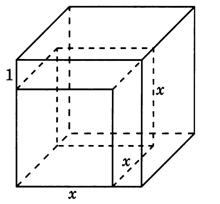
Задание 2.Найдите объём фигуры, изображённой на рисунке. Её основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых рёбер перпендикулярно плоскости основания и равно 3.
Решение
Данный многогранник представляет из себя четырёхугольную пирамиду, в основании которой лежит квадрат со стороной 6, из которой вырезана пирамида, в основании которой находится квадрат со стороной 3, а вершина совпадает с вершиной первой пирамиды. Высотой обеих пирамид является боковое ребро первой пирамиды, по условию, перпендикулярное плоскости основания пирамиды и равное 3. Объём пирамиды находится по формуле
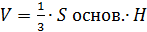
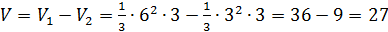
Ответ:27
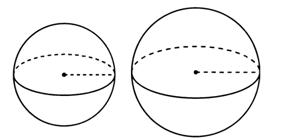
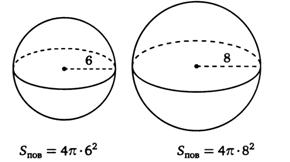
Задание 3. Радиусы двух шаров равны 6 и 8 см. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей данных шаров.
Решение
Площадь поверхности данных шаров равна
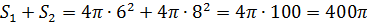
Радиус шара, площадь которого равна сумме площадей поверхностей данных шаров: 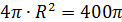
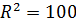
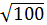
Ответ: 10 см
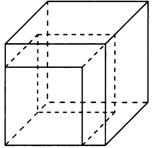
Задание 4.Если каждое ребро куба увеличить на 1, то площадь его поверхности увеличится на 30. Найдите ребро куба и его объём (Рис.1)
Решение
Обозначим ребро куба х (Рис.2). Шесть равных граней куба являются квадратами, поэтому площадь поверхности куба 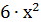
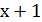
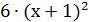
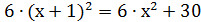
Ответ:2
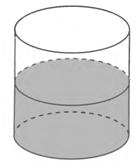
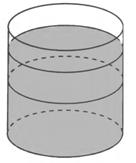
Задание 5.В цилиндрический сосуд. в котором находится 6 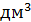
Чему равен объём детали?
Решение
Так как уровень жидкости в сосуде поднялся в 1,5 раза, то и объём увеличился в 1,5 раза ( 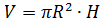
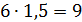
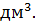
Ответ:
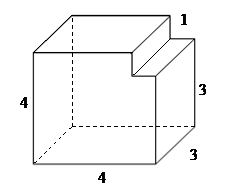
Решение:
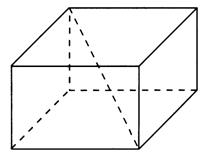
Данный многогранник представляет из себя параллелепипед с объемом V1, из которого удален меньший параллелепипед с объемом V2.
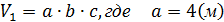
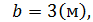
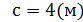
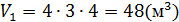
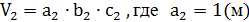
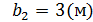
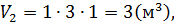
Ответ:
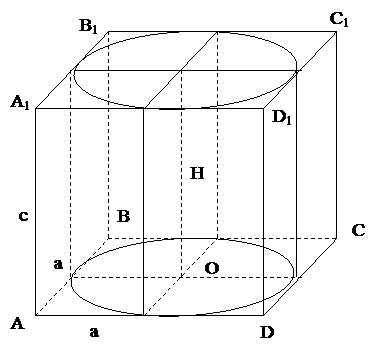
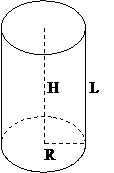
Задание 7.В прямоугольный параллелепипед вписан цилиндр, радиус основания и высота которого равны 5,5 см. Найти объем параллелепипеда и объем цилиндра.
Решение:
Т.к. в прямоугольный параллелепипед вписан цилиндр, то основанием параллелепипеда является квадрат.
 |
 |
 |
Решение:
1. 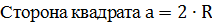
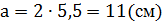
2. Высота параллелепипеда равна высоте вписанного в него цилиндра:
3. Объем прямоугольного параллелепипеда: 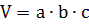
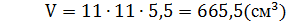
4. Объем цилиндра: 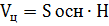
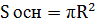
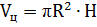
Задание 8.Из параллелепипеда (см. условие предыдущей задачи) был удален цилиндр, найти объем получившейся фигуры и площадь её полной поверхности.
Решение:
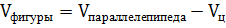
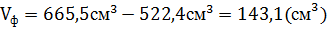
Площадь полной поверхности этой фигуры:
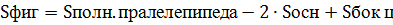
Ответ: 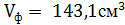
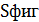
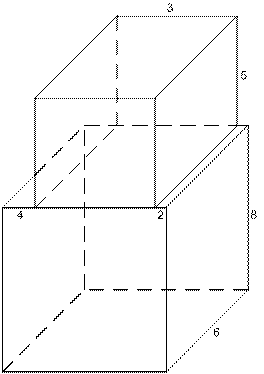
Задание 9.Найти объем и площадь полной поверхности фигуры, изображенной на рисунке :
Решение:
Объём многогранника равен сумме объёмов двух прямоугольных параллелепипедов: 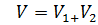
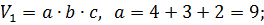
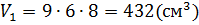
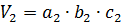
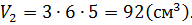
Площадь поверхности фигуры равна сумме площадей поверхности большого параллелепипеда и площади боковой поверхности маленького параллелепипеда:
Ответ: 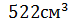
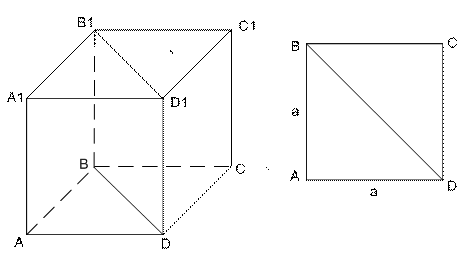
Задание №10.Найти площадь диагонального сечения правильной четырёхугольной призмы, высота которой равна 4 см., а длина стороны основания равна 10 см.
Дано:
Найти:
Решение:
1) Призма правильная, поэтому она прямая, то есть её боковое ребро является высотой:
и в основании призмы лежит квадрат 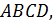
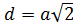
2) Диагональным сечением призмы является прямоугольник 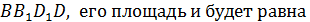
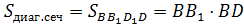
Ответ:
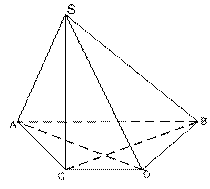
Задача № 11.Прямоугольный треугольник АВС вращается вокруг гипотенузы АВ. Найти объём тела вращения и площадь поверхности тела вращения, если известно угол 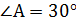
Дано: 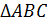
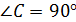
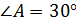
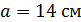
Найти: 1) V т.вр.; 2) S т.вр.
Решение:
1) Фигурой вращения является тело, состоящее из двух конусов с общим основанием.
Образующие конусов: L1 = AC = b; L2 = BC = a = 14 см.
Высоты конусов: Н1 = АО; Н2 = ВО
Радиус основания конусов: R = CO, где CO⊥AB.
2) Решим прямоугольный треугольник АВС: 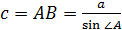
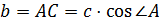
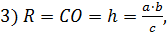
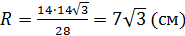
4) Объём тела вращения равен сумме объёмов двух конусов:
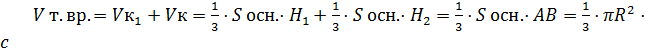
учли, что 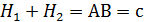
5) Площадь поверхности тела вращения равна сумме площадей боковой поверхности двух конусов:
Ответ:
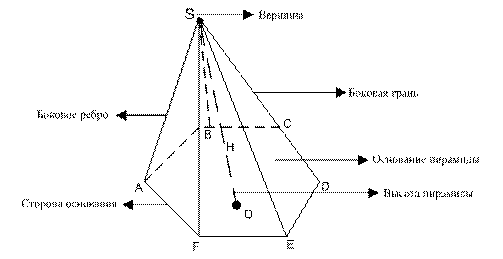
Пирамида
Определение: Пирамидой называется многогранник, в основании которого лежит произвольный многоугольник, а остальные грани являются треугольниками с общей вершиной.
Определение: Высотой пирамиды называется отрезок перпендикуляра, опущенного из вершины пирамиды на плоскость основания пирамиды:
Определение: Диагональная плоскость, это плоскость, проходящая через вершину пирамиды и диагональ основания.
Определение: Диагональное сечение пирамиды- это сечение, которое получается при пересечении пирамиды диагональной плоскостью. (В любой пирамиде, кроме треугольной, диагональное сечение, это треугольник).
Виды пирамид:
I. Треугольная, 4-х, 5-и, 6-и угольная и так далее, в зависимости от многоугольника, лежащего в основании пирамиды.
II. Правильная и неправильная пирамида.
Определение: Пирамида называется правильной, если 1) в основании её лежит правильный многоугольник, 2) вершина пирамиды проектируется в центре основания.
Определение: Апофема- это высота боковой грани правильной пирамиды, проведённая из её вершины на сторону основания пирамиды.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Источник