- Замена переменной в неопределенном интеграле
- Алгоритм метода замены переменной
- Примеры решений
- Метод замены переменной в неопределённом интеграле
- Суть метода замены переменной
- Применяем замену переменной вместе
- Применить замену переменной самостоятельно, а затем посмотреть решение
- Снова применяем замену переменной вместе
- Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле
- Зміст
- Тема 1. Неопределенный интеграл, его свойства
- 1. Первообразная
- 2. Неопределенный интеграл
- 3. Свойства неопределенного интеграла
- 4. Таблица первообразных
- Тема 2. Основные методы интегрирования
- 5. Интегрирование подстановкой (заменой переменной)
- 6. Интегрирование по частям
- 7. Интегрирование простейших рациональных дробей
Замена переменной в неопределенном интеграле
Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ \int f(x) dx $, сделаем замену $ x=\phi(t) $. Отметим, что функция $ \phi(t) $ является дифференцируемой, поэтому можно найти $ dx = \phi'(t) dt $.
Теперь подставляем $ \begin
$$ \int f(x) dx = \int f(\phi(t)) \cdot \phi'(t) dt $$
Эта и есть формула замены переменной в неопределенном интеграле.
Алгоритм метода замены переменной
Таким образом, если в задаче задан интеграл вида: $$ \int f(\phi(x)) \cdot \phi'(x) dx $$ Целесообразно выполнить замену переменной на новую: $$ t = \phi(x) $$ $$ dt = \phi'(t) dt $$
После этого интеграл будет представлен в виде, который легко взять основными методами интегрирования: $$ \int f(\phi(x)) \cdot \phi'(x) dx = \int f(t)dt $$
Не нужно забывать также вернуть замененную переменную назад к $ x $.
Примеры решений
Найти неопределенный интеграл методом замены переменной: $$ \int e^ <3x>dx $$
Выполняем замену переменной в интеграле на $ t = 3x, dt = 3dx $:
$$ \int e^ <3x>dx = \int e^t \frac
Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $:
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
| Пример 2 |
| Ответ |
| $$ \int \sin^5 x \cos x dx =\frac<1><6>\sin x + C $$ |
| Пример 3 | |||||||||
| Найти интеграл с помощью замены переменной: $$ \int \frac<\cos \sqrt | |||||||||
| Решение | |||||||||
| Сайт: | Навчальний сайт ХНАДУ |
| Курс: | Вища Математика (2 семестр) Вишневецький А.Л. |
| Книга: | Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле |
| Надруковано: | Гість |
| Дата: | четвер 18 листопад 2021 07:11 |
Зміст
Тема 1. Неопределенный интеграл, его свойства
1. Первообразная
Пусть f ( x ) – данная функция.
Определение . Функция F ( x ) называется первообразной для f ( x ) , если
Примеры . x 2 – первообразная для 2 x , т.к. ( x 2 )’ = 2 x . Впрочем, x 2 + 1 и x 2 — 5 – тоже первообразные для 2 x , т.к. ( x 2 + 1)’ = 2 x и ( x 2 — 5)’ = 2 x .
Теорема 1. Если F ( x ) – первообразная для f ( x ) , то
1) F ( x ) + С – тоже первообразная для f ( x ) .
2) Любая первообразная для f ( x ) имеет вид F ( x ) + С для некоторого С.
2. Неопределенный интеграл
Определение . Множество всех первообразных функции f ( x ) называется неопределенным интегралом от этой функции и обозначается так:
Здесь f ( x) dx – подынтегральное выражение, f ( x ) – подынтегральная функция, x – переменная интегрирования.
Если функция непрерывна на некотором отрезке, то на этом отрезке существует её неопределенный интеграл.
Операции нахождения дифференциала и неопределенного интеграла – взаимно обратные:
3. Свойства неопределенного интеграла
Формул «интеграл от произведения» и «интеграл от частного» функций нет.
4. Таблица первообразных
Таблица проверяется с помощью (1). Формулы № 10, 12, 14 есть обобщение формул № 9, 11, 13. В формулах № 10, 12, 14, 15 a ≠ 0 .
Полная запись формулы №1:
Тема 2. Основные методы интегрирования
5. Интегрирование подстановкой (заменой переменной)
Суть метода: путем введения новой переменной интегрирования (т.е. подстановки) свести данный интеграл к более простому (желательно – к табличному).
Начнем с формулы замены. Надо найти интеграл
Сделаем подстановку φ(t) = x , где φ(t) — функция, имеющая непрерывную производную. По определению дифференциала, dx = φ'(t)dt . Подставляем в (1):
– формула замены переменной в неопределенном интеграле. После ее применения и вычисления полученного интеграла нужно вернуться к исходной переменной. Формулу (2) применяют как «слева направо», так и «справа налево». Общих методов подбора подстановок не существует.
6. Интегрирование по частям
Теорема . Если функции u = u(x) , ν = ν (x) имеют непрерывные производные, то
Док-во . Интегрируя равенство d(uv) = udv + vdu , получим uv = ∫ udv — ∫ vdu , т.е. (5)
Формула (5) сводит нахождение ∫ udv к нахождению ∫ vdu , поэтому ее применяют тогда, когда последний интеграл не сложнее первого. Для применения этой формулы подынтегральное выражение представляют как произведение двух сомножителей, один из которых обозначают u , другой dv . Затем u дифференцируют (находят du ), а dv интегрируют (находят v ).
Укажем способ выбора u и dv в двух типичных случаях. Пусть P(x) – многочлен.
Формулу (5) можно применять повторно. Например, в случае а) это делают n раз, где n – степень многочлена P(x) .
7. Интегрирование простейших рациональных дробей
Простейшие рациональные дроби – это дроби:
1 рода: ( k N ) и 2 рода: (дискриминант знаменателя D n = 1 так:
- Заменить
- Разложить интеграл в сумму вида
К первому интегралу применить формулу (4), а второй – табличный (арктангенс).
Источник

 можем ввести новую переменную
можем ввести новую переменную  ;
; можем ввести новую переменную
можем ввести новую переменную  ;
; можем ввести новую переменную
можем ввести новую переменную  .
. определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула (1)
(1)


 . Отсюда
. Отсюда  .
.  .
.
 и
и  , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
, это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики. , откуда
, откуда  и
и  .
. , в свою очередь
, в свою очередь  .
.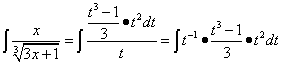 ,
,

 .
. .
. .
. ,
,  ,
,  .
.
 .
. .
. .
. , откуда
, откуда  ,
,  .
.

 .
. , тогда
, тогда  .
.
 .
.


