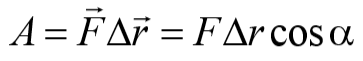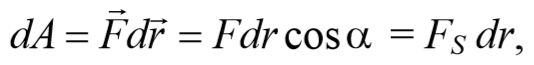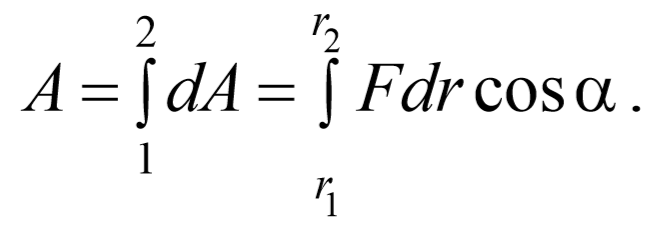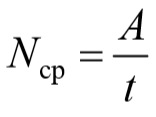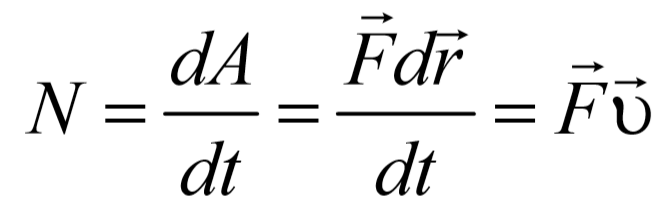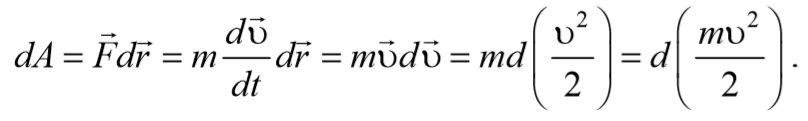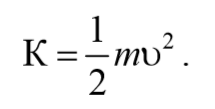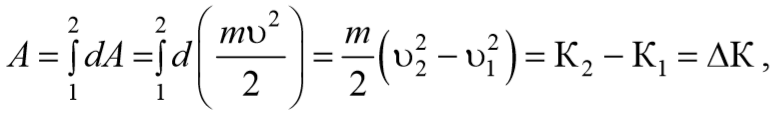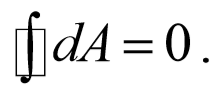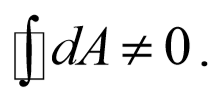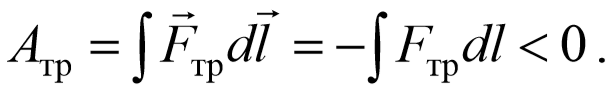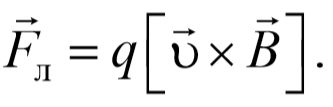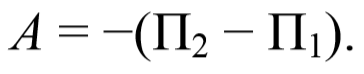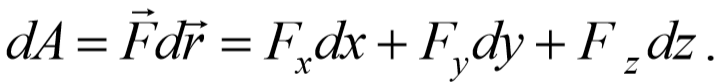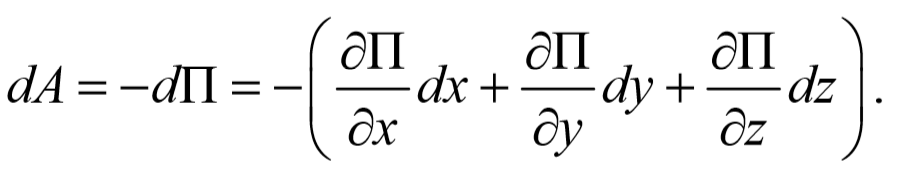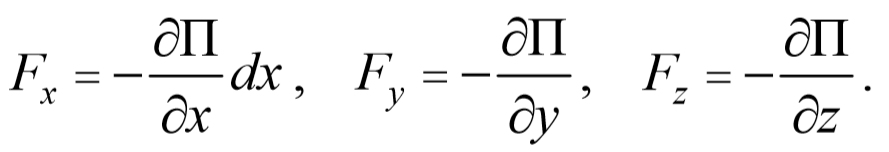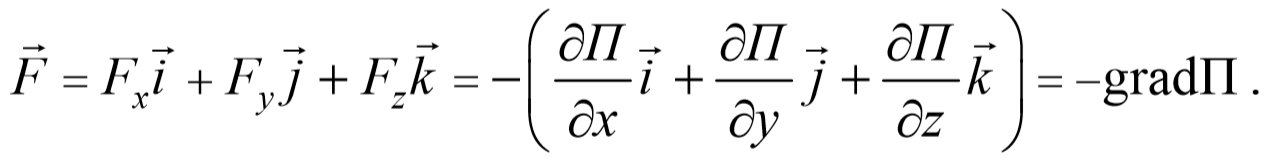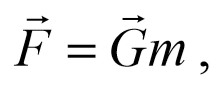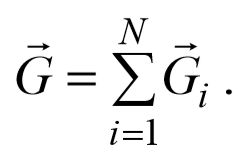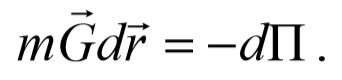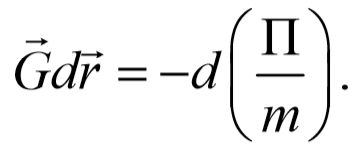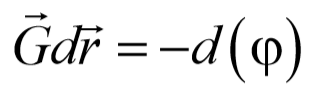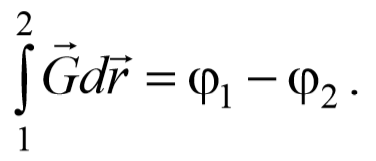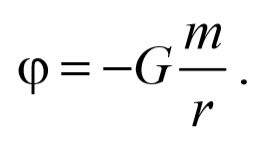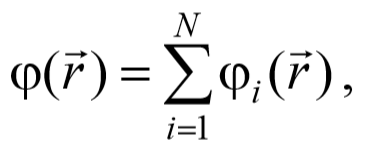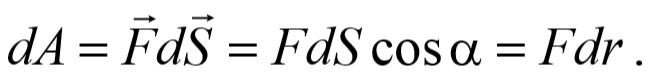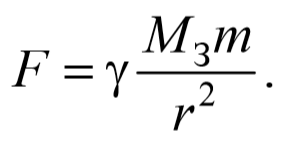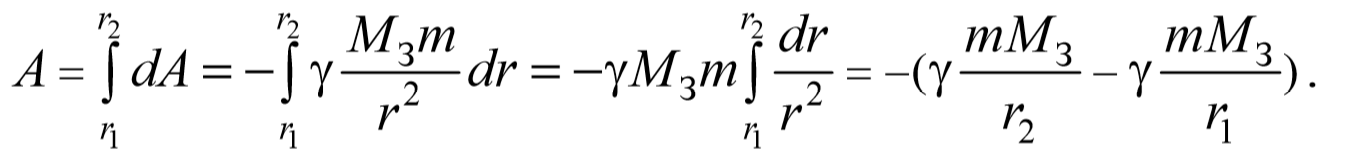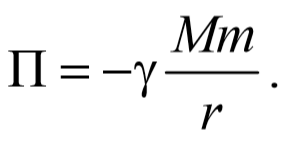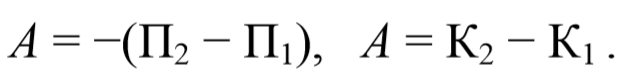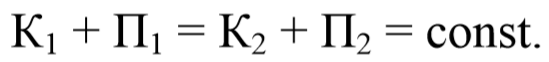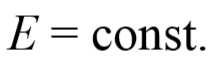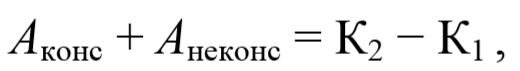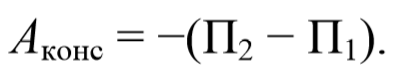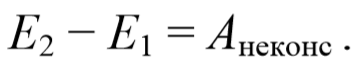- Механическое движение. Траектория. Путь. Перемещение
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Лекция №4. Работа, мощность, энергия
- 3.1. Работа постоянной и переменной силы. Мощность.
- 3.2. Кинетическая энергия. Теорема об изменении кинетической энергии.
- 3.3. Консервативные и неконсервативные силы.
- 3.4. Потенциальная энергия. Связь между силой и энергией потенциального поля.
- 3.5. Гравитационное поле. Работа в гравитационном поле.
- 3.6. Закон сохранения механической энергии.
Механическое движение. Траектория. Путь. Перемещение
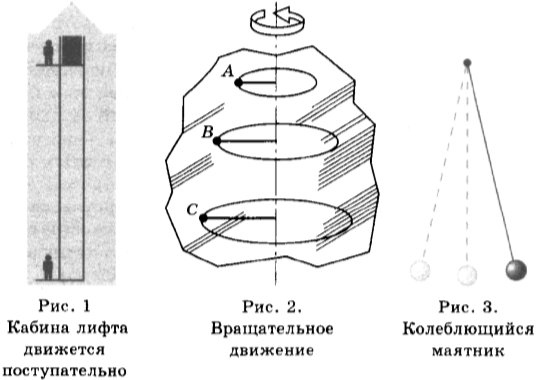
1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).
Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).
Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).
2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.
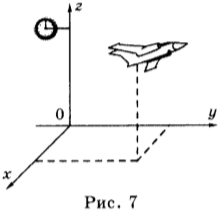
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).
Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.
Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).
3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.
Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.
Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.
Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.
Раздел механики, изучающий способы описания движения тел, называют кинематикой.
4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.
Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.
Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.
Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.
Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.
В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.
Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.
5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.
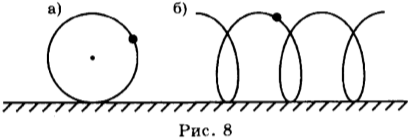
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).
6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.
Если известны траектория тела, его начальное положение и пройденный им путь за время \( t \) , то можно найти положение тела в момент времени \( t \) . (рис. 9)
Путь обозначают буквой \( l \) (иногда \( s \) ), основная единица пути 1 м: \( [\,\mathrm
Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.
7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.
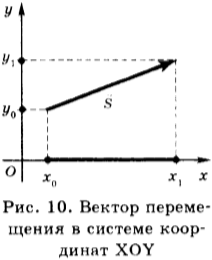
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)
Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается \( \overrightarrow \) . Единица перемещения \( [\,\mathrm\,] \) = 1 м.
Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.
Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.
Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.
При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.
Координаты начала перемещения — \( x_0, y_0 \) ; координаты конца перемещения — \( x_1, y_1 \) . Проекция вектора перемещения на ось ОХ равна: \( s_x=x_1-x_0 \) . Проекция вектора перемещения на ось OY равна: \( s_y=y_1-y_0 \) .
Модуль вектора перемещения равен: \( s=\sqrt
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь \( l \) и модуль перемещения \( s \) мяча за всё время движения?
1) \( l \) = 3,3 м, \( s \) = 3,3 м
2) \( l \) = 3,3 м, \( s \) = 0,7 м
3) \( l \) = 0,7 м, \( s \) = 0,7 м
4) \( l \) = 0,7 м, \( s \) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса \( R \) . Чему равны при этом путь \( l \) и модуль перемещения \( s \) точки обода?
1) \( l=2R \) , \( s=2R \)
2) \( l=\pi R \) , \( s=2R \)
3) \( l=2R \) , \( s=\pi R \)
4) \( l=\pi R \) , \( s=\pi R \) .
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
Источник
Лекция №4. Работа, мощность, энергия
3.1. Работа постоянной и переменной силы. Мощность.
Работа − это количественная характеристика процесса обмена энергией между взаимодействующими телами.
Если тело движется прямолинейно и на него действует постоянная сила, то работа этой силы равна скалярному произведению вектора силы на вектор перемещения:
где α − угол между направлением действия силы и направлением перемещения. Работа измеряется в [ Дж]. 1 Дж − это работа, совершаемая силой в 1 Н на пути в 1 м.
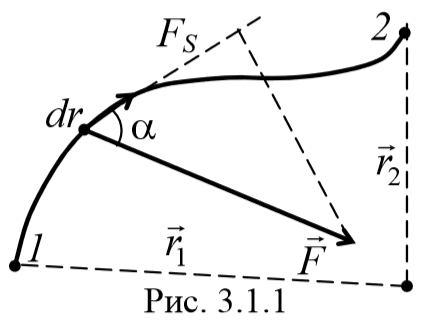
В случае переменной силы водится понятие элементарной работы dA , равной скалярному произведению вектора силы F и вектора элементарного перемещению dr
где Fs − проекция силы на касательную к траектории (рис. 3.1.1).
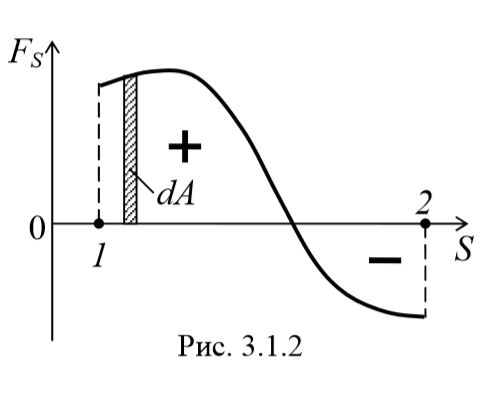
Работа, совершаемая силой на конечном участке пути 1 − 2, равна сумме элементарных работ на отдельных бесконечно малых участках пути (рис. 3.1.2). Она определяется интегралом, вычисленным вдоль участка 1−2 траектории:
Если изобразить график зависимости проекции силы на касательную к траектории от перемещения, то выражение (3.1.3) имеет смысл площади фигуры под кривой.
Для характеристики скорости работы существует мощность. Средняя мощность равна отношению работы к промежутку времени, в течение которого эта работа производится:
Мгновенная мощность , т. е. мощность в данный момент времени определяется как
т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы.
За единицу мощности принимается мощность в 1 Вт, при которой в единицу времени 1 с совершается работа в 1 Дж.
3.2. Кинетическая энергия. Теорема об изменении кинетической энергии.
Рассмотрим понятие кинетической энергии тела. Пусть тело массой m движется поступательно под действием некоторой силы F=m(d υ /dt) (или результирующей нескольких сил). Найдем элементарную работу, которую совершает эта сила на элементарном перемещении d r = υ dt
Отсюда видно, что работа силы F идет на приращение некоторой величины (стоящей в скобках), которую называют кинетической энергией тела. Таким образом, кинетическая энергия − это энергия тела, обусловленная его механическим движением.
Для тела массой m двигающегося поступательно со скоростью υ кинетическая энергия определяется соотношением
Проинтегрировав выражение (3.2.1) от начальной до конечной скорости получим теорему об изменении кинетической энергии
т. е. приращение кинетической энергии тела на некотором перемещении равно работе результирующей всех сил, действующих на тело на том же перемещении.
3.3. Консервативные и неконсервативные силы.
Все силы в механике делятся на консервативные и неконсервативные силы .
В общем случае работа, определяемая выражением (3.1.3), зависит от траектории, которую описывает точка приложения силы. Однако существуют силы (тяготения, тяжести, упругости, электростатические и др., которые являются центральными), работа которых не зависит от формы траектории, а зависит только от начального и конечного положения движущейся точки. Такие силы называются консервативными, а их работа по замкнутому контуру равна нулю
Если работа силы зависит от формы траектории, которую описывает точка приложения силы, то такие силы называются неконсервативными, а их работа по замкнутому контуру не равна нулю
Среди неконсервативных сил выделяют диссипативные и гироскопические силы.
1) Диссипативные силы . К ним относятся, в частности, силы трения и силы сопротивления среды. Полная работа этих сил является отрицательной.
При наличии сил трения и сопротивления энергия механической системы уменьшается, переходя во внутреннюю энергию тел, что приводит к их нагреванию. Такой процесс называют диссипацией энергии, а силы называют диссипативными . Таким образом, сила называется диссипативной, если работа, совершаемая этой силой, зависит от траектории движения тела.
2) Гироскопические силы . Эти силы зависят от скорости движения материальной точки и действуют перпендикулярно к этой скорости. Работа таких сил всегда равна нулю, однако от консервативных сил они отличаются тем, что определяются не только положением точки, но и ее скоростью. Примером такой силы является сила Лоренца. Сила Лоренца − это сила, действующая на заряженную частицу q , движущуюся со скоростью υ , в магнитном поле индукции B
3.4. Потенциальная энергия. Связь между силой и энергией потенциального поля.
Важнейшей составной частью механической энергии является потенциальная энергия , которая определяется как часть общей механической энергии системы, зависящей от взаимного расположения материальных точек системы и их положения во внешнем силовом поле. Из определения следует, что потенциальная энергия системы не должна зависеть от того, каким образом данная конфигурация частиц системы возникла. Это значит, что понятие потенциальной энергии имеет смысл лишь в том случае, когда на материальные точки системы действуют только консервативные силы. Изменение потенциальной энергии системы должно определяться только работой консервативных сил. Другими словами, работа консервативных сил при переходе из состояния 1 в состояние 2 равна убыли потенциальной энергии
Таким образом, силовое поле консервативных сил является потенциальным полем.
Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным . Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.
Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным , а силы, как уже было сказано выше − консервативными. Если это условие не выполняется, то силовое поле не является потенциальным. Силовое поле представляет собой особую форму существования материи, посредством которой осуществляются гравитационное, электромагнитное, ядерное и другие взаимодействия.
Взаимодействие в консервативной системе может быть описано с помощью потенциальной энергии либо с помощью сил взаимодействия точек системы. Поэтому между потенциальной энергией и силой, действующей на материальную точку, должна существовать определенная взаимосвязь. Потенциальная энергия системы является функцией координат П(x,y,z) . Пусть силы, действующие на систему, выполнили элементарную работу
С другой стороны, используя уравнение (3.4.1)
Сравнивая выражения (3.4.2) и (3.4.3), получим выражения для проекций сил поля
Для вектора силы получаем следующее выражение
Смысл градиента станет нагляднее и яснее, если ввести понятие эквипотенциальной поверхности − поверхности, во всех точках которой потенциальная энергия П имеет одно и то же значение. Каждому значению П соответствует своя эквипотенциальная поверхность. Из формул (3.4.4) следует, что проекция вектора на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор нормален эквипотенциальной поверхности в данной точке. Далее, возьмем перемещение в сторону уменьшения П, тогда П F противоположен по направлению вектору grad П, то приходим к выводу, что градиент П − это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии П.
3.5. Гравитационное поле. Работа в гравитационном поле.
Рассмотрим более подробно понятие поля сил. Опыт показывает, что в случае гравитационных взаимодействий сила, действующая на тело (А) массой m со стороны окружающих тел (В), пропорциональна массе. Эта сила может быть представлена в виде произведения двух величии:
где G − некоторый вектор (для гравитационных сил вблизи поверхности Земли он совпадает с вектором ускорения свободного падения), зависящий как от положения тела (А) массой m , так и от свойств окружающих тел (В).
Такое представление силы открывает возможность иной физической интерпретации взаимодействия, связанной с понятием поля. В этом случае говорят, что система тел (В) окружающих тело массой m создает в окружающем пространстве поле, характеризуемое вектором G ( r ) . Иначе можно сказать, что в каждой точке пространства система тел (В) является источником поля и создает такие условия, при которых тело массой m , помещенное в это поле, испытывает действие силы (3.5.1). Причем считают, что поле существует безотносительно к тому, есть ли в нем тело (А) или нет. При переходе к переменным полям выясняется, что понятие поля имеет глубокий физический смысл: поле есть физическая реальность.
Вектор G ( r ) называют напряженностью поля . Если поле образовано несколькими источниками, результирующее поле равно сумме полей, созданных каждым из них. Это утверждение является одним из важнейших свойств полей и напряженность G результирующего поля в произвольной точке
где G i − напряженность поля соответствующего источника в этой же точке, N − число источников поля.
Формула (3.5.2) выражает так называемый принцип суперпозиции (или наложения) полей, который является отражением опытных фактов и дополняет законы механики.
Обратимся теперь к потенциальной энергии тела. Согласно формулам (3.4.1) и (3.5.1), можно записать
Поделим обе части этого уравнения на m
и обозначив П/m=φ , получим
Введенная величина φ( r ) называется потенциалом поля в точке с радиус-вектором r .
Формула (3.5.6) позволяет найти потенциал гравитационного поля. Для этого достаточно вычислить интеграл по произвольному пути между точками 1 и 2 и представить затем полученное выражение в виде убыли некоторой функции, которая и есть потенциал φ( r ) . Так, потенциал гравитационного ноля точечной массы m
Потенциал гравитационного поля является энергетической характеристикой поля. Потенциал поля тяготения − это скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля, или работой по перемещению единичной массы из данной точки поля в бесконечность.
В случае, когда поле создается многими источниками, то результирующий потенциал равен
где φ i − потенциал, создаваемый i − телом в данной точке поля; N − число источников поля.
Потенциал, как и потенциальная энергия, может быть определен только с точностью до прибавления некоторой произвольной постоянной, также совершенно несущественной. Поэтому ее обычно опускают, полагая равной нулю. Таким образом, поле можно описывать или в векторном виде G ( r ) , или в скалярном φ( r ) . Оба способа эквивалентны.
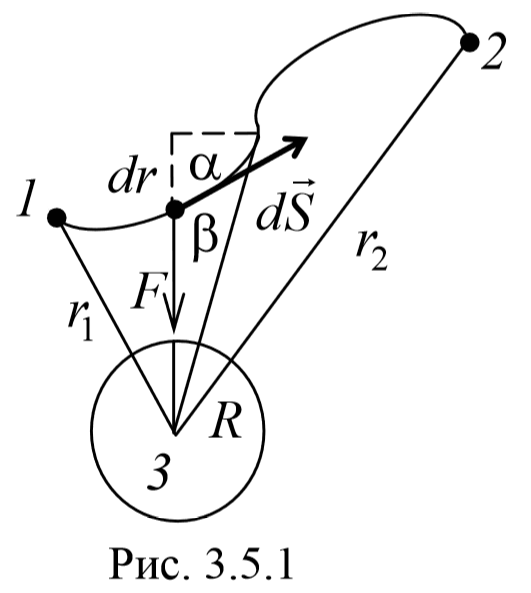
Определим работу, совершаемую силами гравитационного поля Земли при перемещении в нем материальной точки массой m . При перемещении материальной точки на расстояние dS совершается работа
На некотором расстоянии r , согласно закону всемирного тяготения, на тело действует сила
Подставляя (3.5.10) в (3.5.9) и интегрируя в пределах от r1 до r2 , получим
Знак «минус» появляется потому, что направления перемещения и силы противоположны. Из формулы (3.5.10) вытекает, что затраченная работа в поле тяготения не зависит от траектории перемещения, а определяется лишь начальным и конечным положением материальной точки. Следовательно, силы тяготения являются консервативными силами , а поле тяготения является потенциальным . Сравнивая (3.5.11) с (3.4.1) получим, что потенциальная энергия в поле тяготения Земли равна
3.6. Закон сохранения механической энергии.
Пусть на материальные точки системы действуют только консервативные силы. Тогда при переходе системы из одного состояния работа консервативных сил равна
Из (3.6.1) получаем, что
Величину E=K+П называют полной механической энергией системы.
Из соотношения (3.6.2) следует закон сохранения полной механической энергии: полная механическая энергия системы, на материальные точки которой действуют только консервативные силы, с течением времени не изменяется:
Если на систему действуют помимо консервативных сил еще и неконсервативные силы то
а работа консервативных сил равна
Тогда с учетом формулы (3.6.5), выражение (3.6.4) примет следующий вид
В этом случае изменение полной механической энергии системы равно работе неконсервативных сил.
Таким образом, в системе, в которой кроме консервативных сил, действуют также неконсервативные силы, полная механическая энергия системы не сохраняется, и закон сохранения механической энергии не выполняется. Но всегда возникает эквивалентное количество энергии другого вида взамен механической энергии, т. е. выполняется фундаментальный закон сохранения и превращения энергии. Энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
Источник