Назовите способы задания движения точки

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Способы задания движения точки

Для решения задач кинематики необходимо, чтобы изучаемое движение было задано. Оно считается заданным, если в любой момент времени однозначно можно определить положение точки в пространстве относительно заданной системы отсчета. Используют три основных способа задания движения точки: векторный, координатныйи естественный.

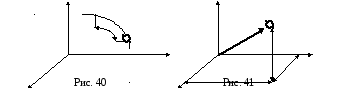
Векторный способ. Положение движущейся точки М в любой момент времени можно определить с помощью ее радиус-вектора, проведенного из центра О, связанного с телом отсчета, в точку М (рис. 1.1). Чтобы задать движение векторным способом, необходимо определить векторную функцию времени в виде:

(1.1)

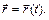
Зависимость (1.1) называют уравнением движения точки в векторной форме. Начало радиус-вектора движущейся точки находится в точке О, а конец его перемещается по траектории вместе с точкой М. Геометрическое место концов радиус-вектора, т.е. годограф этого вектора, определяет траекторию движущейся точки.

Координатный способ. С телом отсчета связывают прямоугольную систему декартовых координат, при этом положение точки определяют ее координатами, которые являются скалярными функциями времени (рис. 1.2):

(1.2)

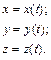
Уравнения (1.2) называют уравнениями движения точки в координатной форме. Они являются параметрическими уравнениями траектории точки. Исключив из этих уравнений параметр – время, можно получить уравнение траектории.

Между способами задания движения точки имеется связь. Так, если начало декартовой системы координат совпадает с центром, из которого проводится радиус-вектор точки при векторном способе изучения ее движения (см. рис. 1.2), то координаты точки равны проекциям на соответствующие оси радиус-вектора точки

,

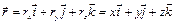
где 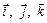– единичные орты координатных осей.

Естественный способ. Этот способ используют в тех случаях, когда заранее известна траектория точки. На траектории выбирают неподвижную точку О (начало отсчета), а также положительное и отрицательное направления отсчета расстояний точки от начала отсчета (рис. 1.3). Тогда положение точки М на траектории будет однозначно определяться зависимостью криволинейной координаты S = ОМ от времени

(1.3)

Связь между координатным и естественным способами определяется выражением

,

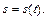
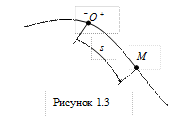
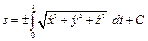
где 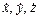– первые производные от координат точки по времени; С – постоянная интегрирования, зависящая от начальных условий.

Источник

Способы задания движения точки

Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех способов: естественный, координатный, векторный.

1. Естественный способ задания движения точки

Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным.

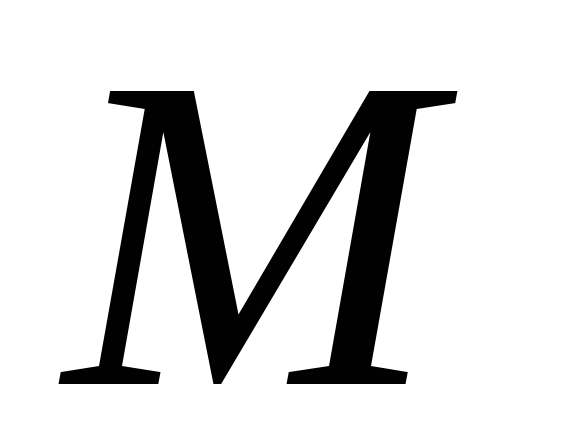
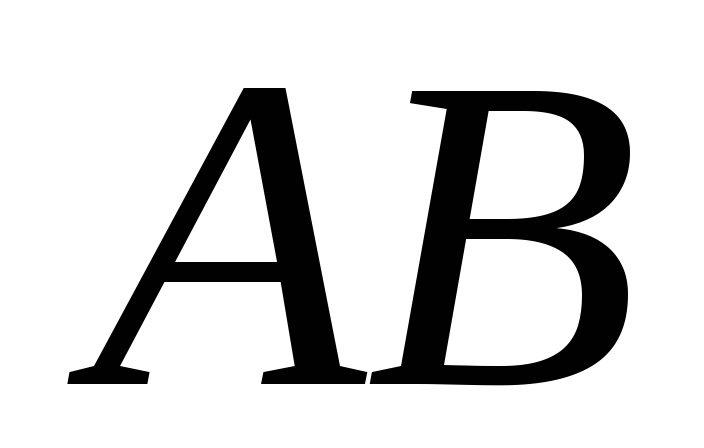
Пусть точка движется относительно системы отсчета вдоль некоторой траектории (рис. 40). Выберем на этой траектории какую-нибудь неподвижную точку , которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.

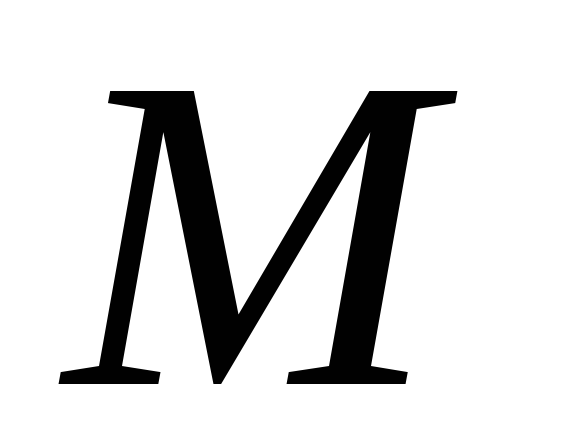
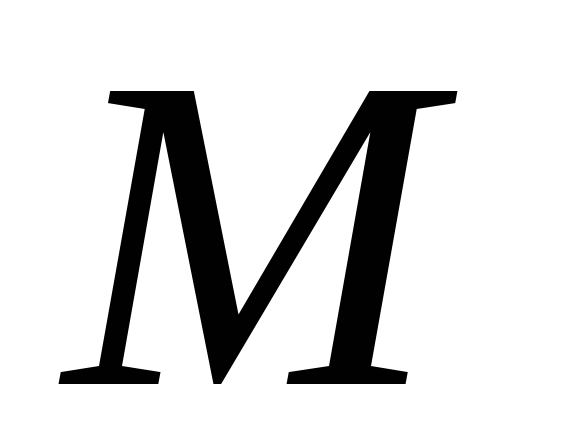
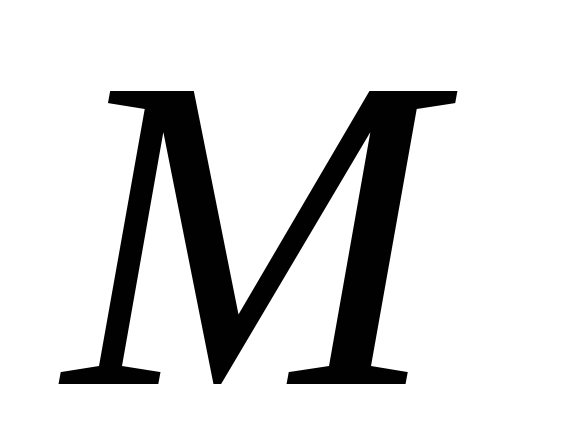
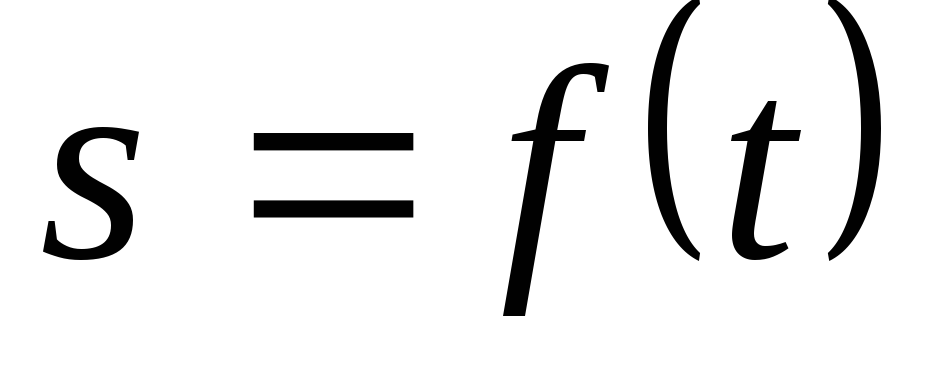
Тогда положение точки на траектории будет однозначно определяться криволинейной координатой , равной расстоянию от точки до точки , измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка будет перемещаться вдоль траектории, следовательно, расстояние будет с течением времени изменяться. Чтобы определить положение точки на траектории в любой момент времени, надо знать зависимость вида:

. (13)

Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным способом, необходимо знать:

1. Траекторию движения точки;

2. Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета;

3. Закон движения точки вдоль траектории .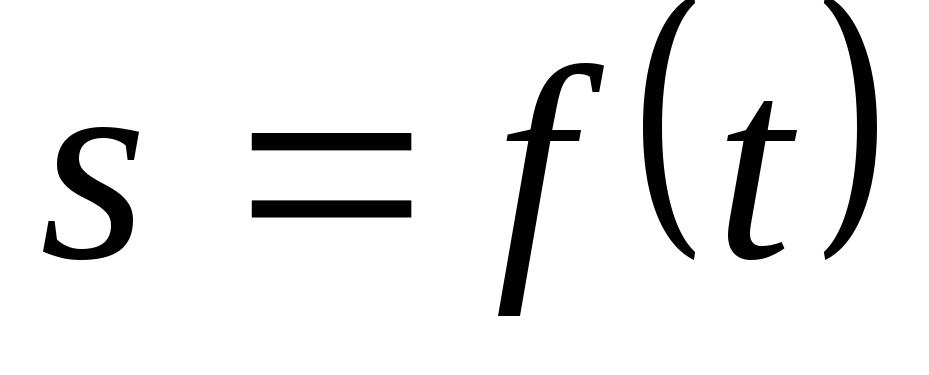

Следует отметить, что величина определяет положение точки, а не пройденный ей путь. Например, если точка, двигаясь из начала отсчета, доходит до положения , а затем, двигаясь в обратном направлении, приходит в положение , то в этот момент ее координата , а пройденный за это время путь будет равен.

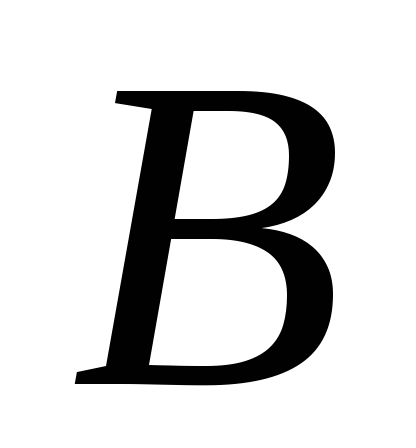
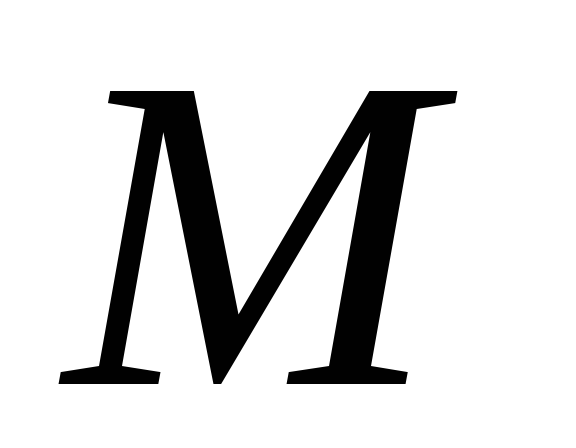
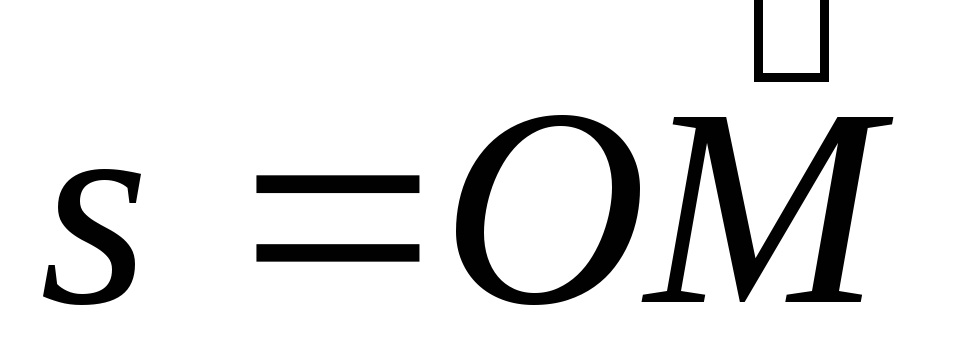
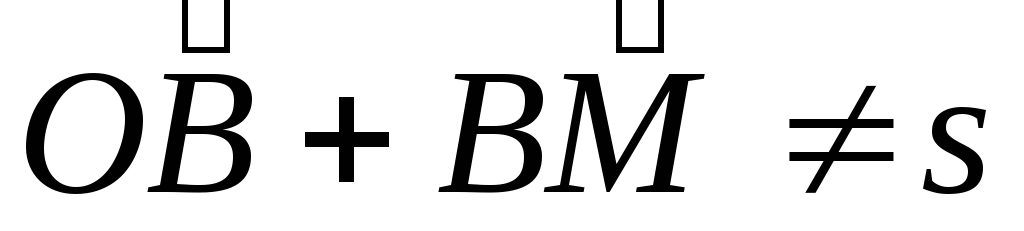
2.Координатный способ задания движения точки

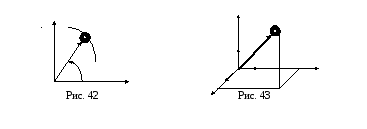
В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде

, ,.(14)

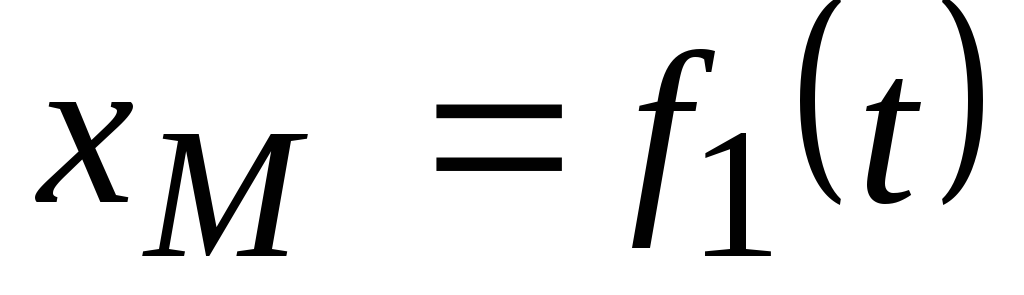
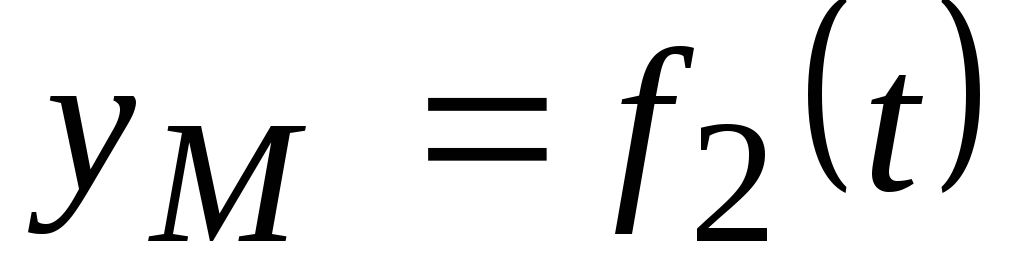
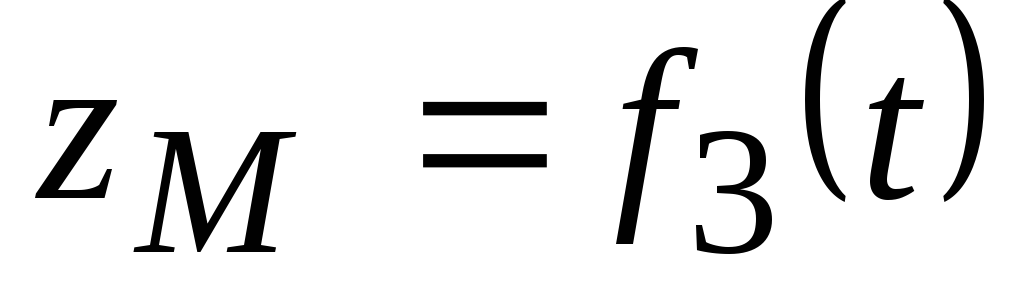
При координатном способе задания движения точки траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами 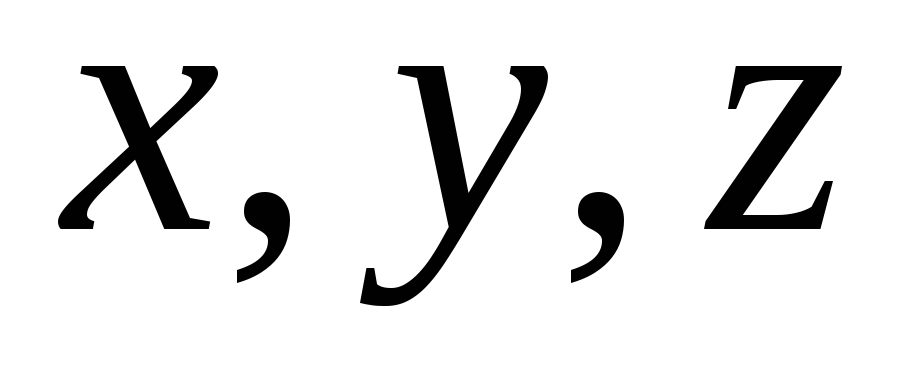, которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.

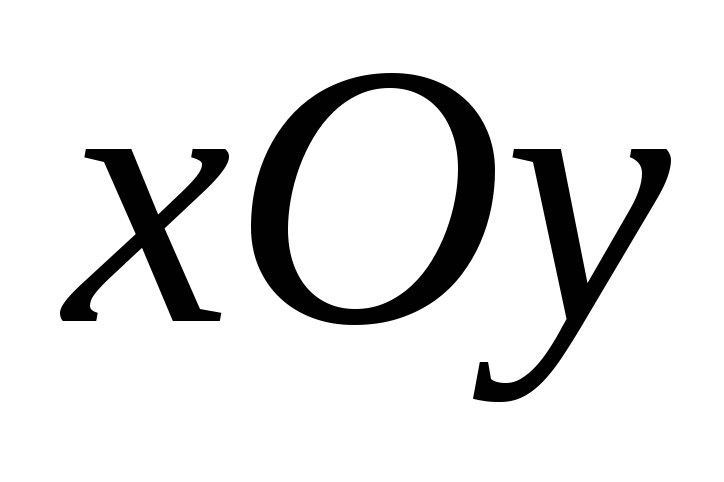
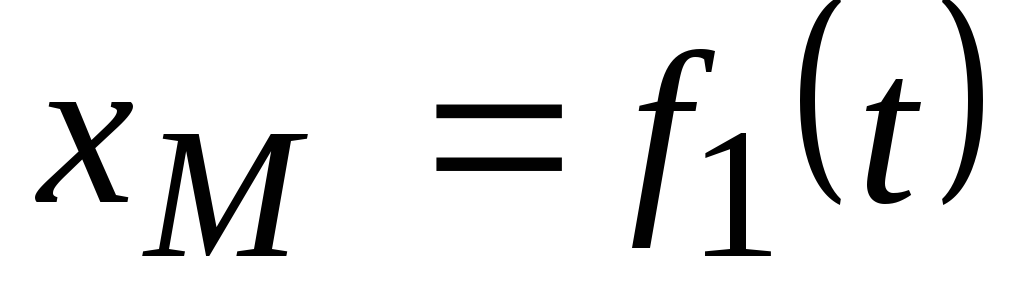
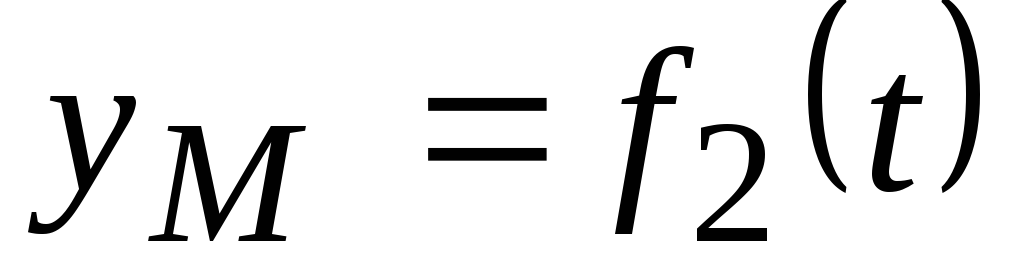
Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную , получаем два уравнения движения,.

Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории.

При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).

Положение точки в этом случае будут определять полярными координатами и, т.е. уравнения движения точки вполярных координатах имеют вид .

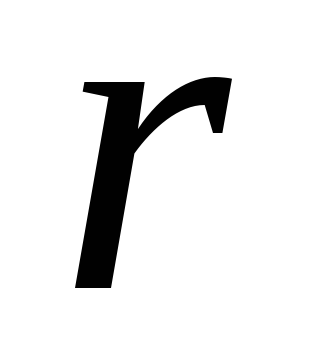
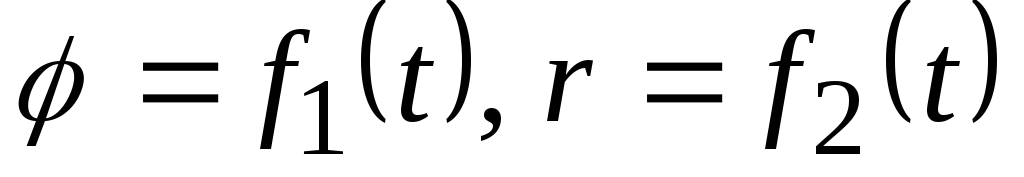
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Тема 1.6. Основные понятия кинематики

§1. Кинематика точки. Введение в кинематику.

Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени.

Механическое движение — это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Тело отсчета — тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел.

Система отсчета — это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).

Рис.1. Система отчета

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t.

Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) — значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Положение тела можно определить с помощью радиус-вектора или с помощью координат.

Радиус-вектор точки М — направленный отрезок прямой, соединяющий начало отсчета О с точкой М (рис. 2).

Координата х точки М — это проекция конца радиуса-вектора точки М на ось Ох. Обычно пользуются прямоугольной системой координат Декарта. В этом случае положение точки М на линии, плоскости и в пространстве определяют соответственно одним (х), двумя (х, у) и тремя (х, у, z) числами — координатами (рис. 3).

Рис.2. Радиус-вектор

Рис.3. Координаты точки М

Материальная точка — тело, размерами которого в данных условиях можно пренебречь.

Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно.

Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движе­нии все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки.

В дальнейшем под словом «тело» будем понимать «материальная точка».

Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. Вид траектории зависит от выбора системы отсчета.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0.Единицы измерения в системе СИ: м (метр).

Перемещение тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка М₀) и конечное (точка М) положение тела (см. рис. 2):

где и — радиус-векторы тела в эти моменты времени.Единицы измерения в системе СИ: м (метр).

Проекция перемещения на ось Ох: ∆r_x =∆х = х-х₀, где x₀ и x — координаты тела в начальный и конечный моменты времени.

Модуль перемещения не может быть больше пути: ≤s.

Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется.

Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:

Видео-урок «Механическое движение»

§2. Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из на­чала координат О в точку М (рис. 4).

Рис.4. Движение точки М

При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента t:

Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки.

Геометрическое место концов вектора , т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.4), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

3. Естественный способ задания движе­ния точки.

Рис.5. Движение точки М

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О’, которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О’ до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂. . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t).

§3. Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий.

Скорость — мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной.

Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с.

Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным.

Для равномерно-прямолинейного движения ∆r=v∆t, где v – постоянный вектор скорости.

Из соотношения видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени.

Источник