Назовите способы проверки правильности вычитания многозначных чисел

Конспект урока с презентацией по математике «Способы проверки правильности результатов вычислений»
план-конспект урока по математике (4 класс) по теме

Познакомить с различными способами проверки результатов вычислений многозначных чисел.

Скачать:

Вложение	Размер
matematika_.docx	25.24 КБ
matematika_.ppt	1.38 МБ

Предварительный просмотр:

Конспект урока математики

Тема: «Способы проверки правильности результатов вычислений»

ЦЕЛЬ УРОКА: познакомить с разными способами проверки правильности результатов.

• создать условия для отработки навыков вычитания многозначных чисел и проверки правильности выполнения вычитания;
• обеспечить усвоение учащимися проверки правильности выполнения вычитания;
• помочь учащимся осознать социальную, практическую и личностную значимость материала.

• познавательные: развивать умение самостоятельно выделять и формулировать познавательную цель; строить математическое высказывание в устной форме; выдвигать гипотезу; устанавливать причинно-следственные связи; делать обобщение; искать и выделять необходимую информацию; моделировать информацию.
• коммуникативные: формировать умение договариваться и приходить к общему решению в совместной деятельности; учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве;
• регулятивные: учить ставить новую учебную задачу в сотрудничестве с учителем; принимать и сохранять учебную задачу; осуществлять контроль по результату и способу действия.

• формировать внутреннюю позицию школьника на уровне положительного отношения к школе; учебно-познавательные мотивы; учебно-познавательный интерес к новому материалу; способность к самооценке на основе критерия успешности учебной деятельности.

ТИП УРОКА: комбинированный

В.Н. Рудницкая,Т.В. Юдачёва, Математика: учебник для 4 класса. Ч. 1. — М.: «Вентана-Граф», 2013г

3.Чтение высказывания «Человеку свойственно ошибаться»

-Это известная латинская фраза. Как вы объясните смысл данной фразы?

-Что мы должны делать, чтобы не ошибаться? (Контролировать свои действия)

-Что должны сделать, чтобы узнать: ошиблись мы или нет? (Уметь проверить)

4. Знакомство со способами проверки

1. По последней цифре.

2. По числу цифр в ответе.

3. Приближенными вычислениями.

4. Выполнением обратного действия.

5. Устные упражнения

1. 28000 + 49000 = 77005

-Верно ли решено данное выражение?

-Как определили? (По последней цифре)

-Чему равна сумма? (77000)

2. 8400 : 4 = 210 (2100)

-Какой способ можно использовать при проверке? (По числу цифр в частном)

3. 300 х 19 = 5000 (5700 )

-Как можно проверить? (Приближенным вычислением)

-Что мы округлим?

300 х 20 = 6000 6000 – 300 = 5700

4. 250 х 40 = 10000

-Что используем при проверке? (Обратное действие)

-Каким способом мы пользуемся чаще всего? (Выполнение обратного действия)

6. Выполнение № 9 с проверкой (на деление)

12. 587 x 6=75.522

41.005 x 3=123.015

5 072 x 4= 20. 288

1 364 x 2 = 2.728

60. 005 x 3=180.015

110.084 x 4=440.336

40.003 x 8=320.024

7. Решение задачи №8 стр.153

1)2.532 X 3 = 7.596 ( деталей) в большом ящике

2)2.532 x 7 = 17.724 (деталей) в маленьком ящике

3)7.596 x10 = 75.960 (деталей) в большом ящике

17.724 +75.960 = 936.840 ( деталей) всего

140 + 280 = 420 (руб) – было всего у покупателя.

8. Решение задачи №11 стр.153

1)950 x 3= 2.850 (км) пролетел за 3 ч

2) 650 x 2= 1300 (км) пролетел за 2

3)2.850 +1.300 = 4.150(км)

9.Итог урока. Рефлексия

Дети на карточках пишут:

Мне было интересно _________________________

Я сегодня понял (а) __________________________

Мне было трудно ____________________________

Я хочу научиться ____________________________

10.Выставление оценок за урок

Предварительный просмотр:

Подписи к слайдам:

Каждому человеку свойственно ошибаться, но только … повторяют свои ошибки. Марк Ту́ллий Цицеро́н древнеримский политический деятель, оратор и философ

ТЕМА: « СПОСОБЫ ПРОВЕРКИ ПРАВИЛЬНОСТИ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ» УРОК МАТЕМАТИКИ

ЦЕЛЬ УРОКА: Познакомиться с разными способами проверки правильности результатов вычислений.

Способы проверки 1. По последней цифре. 2. По числу цифр в ответе. 3. Приближенными вычислениями. 4. Выполнением обратного действия.

Давайте подумаем 28000 + 49000 = 77005 -Верно ли решено данное выражение? -Как определили? (По последней цифре) -Чему равна сумма? (77000)

Давайте подумаем 8400 : 4 = 210 -Верно ли решено данное выражение? -Как определили? (По числу цифр в частном) -Чему равно частное? (2100)

Давайте подумаем -Верно ли решено данное выражение? -Как определили? (Приближенным вычислением, округлением) -Чему равно произведение? 5700 300 х 19 = 5000

Давайте подумаем -Верно ли решено данное выражение? -Как проверить? (Обратным действием) -Чему равно произведение? 10000 250 х 40 = 10000

Реши примеры и проверить ответ 1.258 x 7 = 8.806 12. 587 x 6=75.522 41.005 x 3=123.015 5 072 x 4= 20 . 288 1 364 x 2 = 2.728 973 x 5 = 4 865 60 . 005 x 3= 180.015 110 . 084 x 4=440.336 40.003 x 8=320.024

Реши задачу В вагон погрузили 10 больших и 7 маленьких ящиков. В маленьком ящике помещается 2.532 детали, а в большом ящике таких деталей в 3 раза больше. Сколько всего деталей погрузили в вагон?

Проверь решение 1)2.532 х 3 = 7.596 ( деталей) в большом ящике 2)2.532 x 7 = 17.724 (деталей) в маленьком ящике 3)7.596 x 10 = 75.960 (деталей) в большом ящике 4)17.724 +75.960 = 936.840 ( деталей) всего 5)140 + 280 = 420 (руб.) – было всего у покупателя.

Реши задачу Турист пролетел 3 ч на самолёте Ту-154 со скоростью 950 км/ч и 2 ч на самолёте Ан-24 со скоростью 650 км/ч. Сколько всего километров пролетел турист?

Проверь решение 1)950 x 3= 2.850 (км) пролетел за 3 ч 2) 650 x 2= 1300 (км) пролетел за 2 3)2.850 +1.300 = 4.150(км)

Источник

Лекция 41. Алгоритмы арифметических действий над целыми неотрицательными числами в десятичной системе счисления

1. Алгоритм вычитания

2. Алгоритм умножения

3. Алгоритм деления

2. Решение примеров.

Алгоритм вычитания

Вычитание однозначного числа b из однозначного или двузначно­го числа а, не превышающего 18, сводится к поиску такого числа с, что b + с = а, и происходит с учетом таблицы сложения однозначных чисел.

Если же числа а и b многозначные и b 2 + 8∙10 + 5)-(2∙10 2 + 3∙10 + 1). Чтобы вычесть из числа 4∙10 2 + 8∙10 + 5 сумму 2∙10 2 + 3∙10 + 1, достаточно вычесть из него каждое слагаемое этой суммы одно за другим, и тогда:

(4∙10 2 + 8∙10 + 5) – (2∙10 2 + 3∙10 + 1) =

(4∙10 2 + 8∙10 + 5) – 2∙10 2 — 3∙10 — 1.

Чтобы вычесть число из суммы, достаточно вычесть его из какого-либо одного слагаемого (большего или равного этому числу). Поэтому число 2∙10 2 вычтем из слагаемого

4∙ 10 2 , число 3∙10 — из слагаемого 8∙10, а число 1 — из слагаемого 5, тогда:

(4∙10 2 + 8∙10 + 5) – 2∙10 2 — 3∙10 – 1 =

(4∙10 2 – 2∙10 2 ) + (8∙10 — 3∙10) + (5 – 1)

Воспользуемся дистрибутивностью умножения относительно вычита­ния и вынесем за скобки 10 2 и 10. Тогда выражение будет иметь вид: (4 — 2) ∙10 2 + (8 — 3) ∙ 10 + (5 — 1). Видим, что вычитание трехзначного числа 231 из трехзначного числа 485 свелось к вычитанию однозначных чисел, изображенных цифрами соответствующих разрядов в записи заданных трехзначных чисел. Разности 4-2, 8-Зи5-1 находим по таблице сложения и получаем выражение: 2∙10 2 + 5∙10 + 4, которое является записью числа 254 в десятичной системе счисления. Таким об­разом, 485 — 231 = 254. Выражение (4 — 2) ∙10 2 + (8 — 3) ∙ 10 + (5 — 1) задает правило вычитания, которое обычно выполняется столбиком:

_485

231

Видим, что вычитание многозначного числа из многозначного основывается на:

— способе записи числа в десятичной системе счисления;

— правилах вычитания числа из суммы и суммы из числа;

— свойстве дистрибутивности умножения относительно вычитания;

— таблице сложения однозначных чисел.

Нетрудно убедиться в том, что если в каком-нибудь разряде умень­шаемого стоит однозначное число, меньше числа в том же разряде вычитаемого, то в основе вычитания лежат те же теоретические факты и таблица сложения однозначных чисел. Найдем, например, разность чисел 760 — 326. Воспользуемся правилом записи чисел в десятичной системе счисления и представим эту разность в таком виде:

760 — 326 = (7∙10 2 + 6∙10 + 0) – (3∙10 2 + 2∙10 + 6)

Поскольку из числа 0 нельзя вычесть 6, то выполнить вычитание аналогичное тому, как было сделано в первом случае, невозможно. Поэтому возьмем из числа 760 один десяток и представим его в виде 10 единиц — десятичная система счисления позволяет это сделать — тогда будем иметь выражение: (7∙10 2 + 6∙10 + 0) – (3∙10 2 + 2∙10 + 6).

Если теперь воспользоваться правилами вычитания суммы из числа и числа из суммы, а также дистрибутивностью умножения относительно вычитания, то получим выражение (7 — 3) ∙10 2 + (5 — 2) ∙10 + (10 — 6) или 4∙10 2 + 3∙10+4. Последняя сумма есть запись числа 434 в десятичной системе счисления. Значит, 760 — 326 = 434.

Рассмотрим процесс вычитания многозначного числа из многозначного в общем виде.

Пусть даны два числа

Эта формула задает алгоритм вычитания, но при условии, что для всех к выполняется условие а_к > b_к. Если же это условие не выполняется, то берем наименьшее к, для которого

а_к к и а_т ≠ 0, а а_т-1 = . = а_к+1 = 0. Имеет место равенство а_т ·10 т = (а_т — 1) ·10 т + 9_· 10 т-1 + . + 9_· 10 к+1 +10·10 (например, если т = 4, к = 1, а_т = 6, то 6∙10⁴ = 5∙10⁴ + 9∙10³+9∙10²+10·10). Поэтому в равенстве (1) выражение (am — b m ) ·10 т +…+ (a к — b к) ·10

можно заменить на (am — b m — 1) · 10 т + (9 — b m-1) ·10 + … + (9 — b к+1) ·10 + (a к+10 — b к) ·10 .

Из того, что а_к n +…+ (am — b m — 1) ·10 т + (9 — b m-1) ·10 + . + (9 — b к+1) ·10 +

(a к+10 — b к) ·10 +…+.( а₁ — b₁ ) _·10 + ( а₀ — b₀) все коэффициенты с индексом, мень­шим т, неотрицательны и не превосходят 9. Применяя далее те же пре­образования к коэффициентам a_n — b_n, . am — b m — 1, через п шагов при­дем к записи разности х — у в виде

где для всех к выполняется неравенство 0 а₀, а цифра десятков уменьшаемого отлична от нуля, то уменьшаем цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитаем из числа 10 + а₀ число b₀ и записываем разность в разряде единиц искомого числа, далее переходим к следующему разряду.

4. Если цифра единиц вычитаемого больше цифры единиц умень­шаемого, стоящие в разряде десятков, сотен и т.д. уменьшаемого, равны нулю, то берем первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшаем ее на 1, вес цифры в младших разрядах до разряда десятков включительно увеличиваем на 9, а цифру в разряде единиц на 10: вычитаем b₀ из 10 + а₀, записываем разность в разряде единиц искомого числа и переходим к следующему разряду.

5. В следующем разряде повторяем описанный процесс.

6. Вычитание заканчивается, когда производится вычитание из старшего разряда уменьшаемого.

Упражнения

1. На примере нахождения разности чисел 469 и 246, 757 и 208 про­иллюстрируйте теоретические основы алгоритма вычитания чисел столбиком.

2. Выполните вычитание, используя запись и объясняя каждый шаг алгоритма:

а) 84072 — 63894; в) 935204 — 326435;

б) 940235 — 32849; г) 653481 — 233694.

3. Сколько пятизначных чисел можно записать, используя цифры 1 и 0? Чему равна разность между наибольшим и наименьшим из этих пятизначных чисел?

4. Назовите способы проверки правильности вычитания многозначных чисел и дайте им обоснование.

5. Вычислите (устно) значение выражения, использованные приемы обоснуйте:

в) (7929 + 5027 + 4843) — (2027 + 3843).

6. Докажите, что а + (b-с) =

(а + b) — с, если b ≥ с,

(а — c) + b, если а ≥ с, b ≥ с

Используя это правило, вычислите значение выражения:

а) 6420+ (3580-1736);

б) 5480 + (6290 — 3480).

7. Докажите, что а-(b -с) =

(а — b) + с, если b ≥ с, а ≥ b

(а + c) — с, если b ≥ с, b ≥ а+ с

Используя это правило, вычислите значение выражения:

8. Докажите, что (а — b) — с =

(а — с) — b , если а ≥ с, а ≥ b

а – (b + c), если а ≥ b + с

Используя это правило, вычислите значение выражения:

а) (4317 -1928) -317;

9. Не выполняя вычислений, найдите пары выражений, значения
которых равны:

а) 6387 — 1486 — 821; г) 6387 — 1486 + 821;

б) 6387 — (1486 — 821); д) 6387 + 1486 — 821;

в) 6387 — (1486 + 821); е) 6387 + (1486 — 821).

10. Как изменится разность, если:

а) уменьшаемое уменьшить на 277, а вычитаемое увеличить на 135;

б) к уменьшаемому и вычитаемому прибавить 198;

в) к уменьшаемому прибавить, а из вычитаемого вычесть 198?

11. Решить следующие задачи арифметическим методом, решение запишите в виде числового выражения; выбор действий обоснуйте, используя соответствующую математическую теорию:

а) Первый овощной магазин получил с базы на 500 кг овощей больше, чем второй магазин. Первый магазин продал за день 1 т 300 кг овощей, второй 1 т 100 кг. На сколько меньше овощей осталось к концу дня во втором магазине?

б) В двух мешках лежат яблоки; в первом мешке на 70 яблок больше, чем во втором. В каком мешке яблок будет меньше и на сколько, если переложить из первого мешка во второй 45 яблок?

в) В первой библиотеке 6844 книги, что на 959 книг меньше, чем во второй, а в третьей на 2348 книг меньше, чем в первой и второй библио­теках вместе. Сколько книг в третьей библиотеке?

Алгоритм умножения

Умножение однозначных чисел можно выполнить, основываясь на определении этого действия. Но чтобы всякий раз не обращаться к определению, все произведения однозначных чисел записывают в особую таблицу, называемую таблицей умножения однозначных чи­сел, и запоминают.

Естественно, что смысл умножения сохраняется и для многознач­ных чисел, но меняется техника вычислений. Произведение много­значных чисел, как правило, находят, выполняя умножение столби­ком, по определенному алгоритму. Выясним, каким образом возника­ет этот алгоритм, какие теоретические факты лежат в его основе.

Умножим, например, столбиком 428 на 263.

Видим, что для получения ответа нам пришлось умножить 428 на 3, 6 и 2, т.е. умножить многозначное число на однозначное; но, умножив на 6, результат записали по-особому, поместив единицы числа 2568 под десятками, так как умножали на 60 и получили число 25680, но нуль в конце записи опустили. Слагаемое 856 — »то результат умножения на 2 сотни, т.е. число 85600. Кроме того, нам пришлось найти сумму многозначных чисел.

Итак, чтобы выполнять умножение многозначного числа на мно­гозначное, необходимо уметь:

умножать многозначное число на однозначное и на степень десяти;

складывать многозначные числа.

Сначала рассмотрим умножение многозначного числа на однозначное. Умножим, например, 428 на 3. Согласно правилу записи чи­сел в десятичной системе счисления, 428 можно представить в виде 4∙10² + 2∙10 + 8 и тогда 428∙3 = (4∙10² + 2∙10 + 8) ∙ З; На основании дистрибутивности умножения относительно сложения раскроем скобки: (4∙10²) ∙ З + (2∙10)∙ З + 8 ∙ З

Произведения в скобках могут быть найде­ны по таблице умножения однозначных чисел. Видим, что умножение многозначного числа на однозначное свелось к умножению однозначных чисел. Но чтобы получить окончательный результат, надо преобразовать выражение 12∙10² + 6∙10 + 24 — коэф­фициенты перед степенями 10 должны быть меньше 10. Для этого представим число 12 в виде 1 • 10 + 2, а число 24 в виде 2•10 + 4. Затем раскроем скобки и на основании ассоциативности сложения и дистрибутивности умножения относительно сложения сгруппируем слагаемые.

Таким образом, умножение многозначного числа на однозначное основывается на:

— записи чисел в десятичной системе счисления;

— свойствах сложения и умножения;

— таблицах сложения и умножения однозначных чисел.

Выведем правило умножения многозначного числа на однозначное в общем виде. Пусть требуется умножить х = х= a_n ·10 n + a _n-1 ·10 n -1 + . +а_1·10 + а_0,

на однозначное число у:

причем преобразования выполнены на основании свойств умножения. После этого, используя таблицу умножения, заменяем все произведе­ния а_к ∙ у =b _к∙∙10 + с и получаем:

По таблице сложения заменяем суммы ск + b к-1, где 0 £ к £ n и к: = 0, 1, 2, . n, их значениями. Если, например, с ₀ одно­значно, то последняя цифра произведения равна с ₀. Если же с ₀ = 10 + m ₀, то последняя цифра равна m ₀, а к скобке ( с₁ + b₀ ) надо прибавить 1. Продолжая этот процесс, получим десятичную запись числа х ∙ у.

Описанный процесс позволяет сформулировать в общем виде ал­горитм умножения многозначного числа х = а_n а _n-1 …а₁ а₀ на однозначное число у.

1. Записываем второе число под первым.

2. Умножаем цифры разряда единиц числа х на число у. Если произведение меньше 10, его записываем в разряд единиц ответа и пере­ходим к следующему разряду (десятков).

3. Если произведение цифр единиц числа х на число у больше или равно 10, то представляем его в виде 10 q₁ + c₀; , где c₀ – однозначное число; записываем c₀ в разряд единиц ответа и запоминаем q₁ — пере­нос в следующий разряд.

4. Умножаем цифры разряда десятков на число у, прибавляем к по­лученному произведению число q₁ и повторяем процесс, описанный в пп. 2 и 3.

5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда.

Как известно, умножение числа х на число вида 10 сводится к приписыванию к десятичной записи данного числа к нулей. Покажем это. Умножим число )

х = a_n ·10 n + a _n-1 ·10 n -1 + . +а_1·10 + а₀ на 10 :

(a_n ·10 n + a _n-1 ·10 n -1 + . +а_1·10 + а₀)×10

Полученное выражение является суммой разрядных слагаемых числа

a_n ·10 n + + a _n-1 ·10 n + -1 + . + а_{0 ·} 10 + 0 × 10 + 0 × 10 +…+ 0 × 10 + 0.

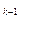
Например, 347 × 10 ³ ⁵⁴ = (3× 10 ² + 4 ×10 + 7) × 10 ³ = 3 × 10 ⁵ + 4 × 10 ⁴ + 7 × 10 ³ + 0 × 10 ² + 0 × 10 + 0 = 347000.

Заметим еще, что умножение на число у × 10 , где у — однозначное число, сводится к умножению на однозначное число у и на число 10 . Например, 52 × 300 = 52 × (3 × 10 ² ) = (52× 3) = 156 × 10 ² = 15600.

Рассмотрим теперь алгоритм умножения многозначного числа на многозначное. Обратимся сначала к примеру, с которого начинали, т.е. к произведению 428 × 263. Представим число 263 в виде суммы 2× 10 ² + 6 ×10 + 3 и запишем произведение 428 × (2× 10 ² + 6 ×10 + 3 ). Оно, согласно дистрибутивности умножения относительно сложения, равно 428 × (2× 10 ²) + 428 × (6 ×10 ) + 428 × 3 . Отсюда, применив ассоциативное свойство умножения, получим: (428 × 2) × 10 ² + (428 × 6) ×10 + 428 × 3 . Видим, что умножение многозначного числа 428 на многозначное число 263 свелось к умножению многозначного числа 428 на однозначные числа 2, 6 и 3, а также на степени 10.

Рассмотрим умножение многозначного числа на многозначное в общем виде. Пусть х и у — многозначные числа, причем у

у = b ·10 + b ·10 + . + b_1·10 + b_0,

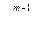
В силу дистрибутивности умножения относитель­но сложения, а также ассоциативности умножения можно записать: х × у = (х · b ·10 + b ·10 + . + b_1·10 + b₀ ) =

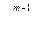
(х · b ) ·10 + (х · b ) ·10 + . + (х · b₁) _· 10 + х · b₀ . Последовательно умножая число х на однозначные числа b , b , . , b₁ , b_0, а затем на степени 10,

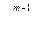
получаем слагаемые, сумма которых равна х · у.

Сформулируем в общем виде алгоритм умножения числа х на число у.

1. Записываем множитель х и под ним второй множитель у.

2. Умножаем число х на младший разряд b₀ числа у и записываем произведение х · b₀ под числом у.

3. Умножаем число х на следующий разряд b₁ числа у и записыва­ем произведение х · b₁, но со сдвигом на один разряд влево, что соот­ветствует умножению х · b₁ на 10.

4. Продолжаем вычисление произведений до вычисления х · bк.

5. Полученные к + 1 произведения складываем.

Изучение алгоритма умножения многозначных чисел в начальном курсе математики, как правило, проходит в соответствии с выделенны­ми этапами. Различия имеются только в записи. Например, при обосно­вании случая умножения многозначного числа на однозначное пишут:

428 × 3 = (400 + 20 + 8) × 3 = 400 × 3 + 20 × 3 + 8 × 3 = 1200 + 60 + 24 = 1284. Основой выполненных преобразований являются:

— представление первого множителя в виде суммы разрядных слагаемых (т.е. запись числа в десятичной системе счисления);

правило умножения суммы на число (или дистрибутивность умножения относительно сложения);

умножение «круглых» (т.е. оканчивающихся нулями) чисел на однозначное число, что сводится к умножению однозначных чисел.

Упражнения

1. На примере умножения числа 357 на 4 проиллюстрируйте теоре­тические основы алгоритма умножения многозначного числа на однозначное.

2. На примере умножения 452 на 186 проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на многозначное.

3. Объясните, почему нижеприведенные задачи решаются при по­мощи умножения чисел и решите их.

а) Земля при обращении вокруг Солнца за сутки проходит пример­но 2 505 624 км. Какой путь проходит Земля за 365 дней?

б) В школу привезли 56 пачек книг, по 24 книги в каждой пачке. Сколько всего книг привезли в школу?

4. Решение задачи запишите в виде числового выражения, а затем найдите его значение:

а) На элеватор отвезли 472 т овса, ржи на 236 т больше, чем овса, а пшеницы в 4 раза больше, чем овса и ржи вместе. Сколько тонн пшеницы отвезли на элеватор?

б) Столяр делает в день 18 рам, а его помощник на 4 рамы меньше. Сколько рам они сделают за 24 дня, если каждый день будут работать вместе?

5. Как могут рассуждать учащиеся, выполняя следующее задание:
«Ширина земельного участка прямоугольной формы равна 24 м. Это в 6 раз меньше его длины. Объясни, что обозначают выражения, записанные по условию задачи, и вычисли их значения: 24 × 6; 24× (24× 6); (24 + 24 × 6) × 6; 24 × 2; 24× 2 + 24 × 6 × 2».

6. Выполните умножение чисел, используя запись столбиком, и объясняя каждый шаг алгоритма:

а) 984 × 27; в) 7040 × 234;

6) 8276 × 73; г) 4569 × 357.

7. Используя свойства умножения, найдите наиболее рациональ­ным способом значение выражения:

а) 8× 13 × 4125× 25; г) 124× 4 + 116× 4;

б) 24× (27 × 125); д) (3750 — 125) × 8;

в) (88 + 48) × 125; е) 1779× 1243 – 779× 1243.

8. Зная, что 650-34 = 22100, найдите произведение чисел, не выпол­няя умножения столбиком:

а) 650 • 36; б) 650 • 32; в) 649•34.

9. Найдите и обоснуйте приемы умножения 24 на 35 и, пользуясь ими, умножьте на 35 числа: 12, 18, 24, 32, 48, 64.

10. Вычислите рациональным способом значение выражения:

а) (420 -394) • 405 – 25 • 405;

б) 105 • 209 + (964 — 859) • 209 • 400.

11. Найдите значения выражений 13•11, 27•11, 35•11, 43•11, 54•11.
Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа меньше 10, достаточно между цифрами данного числа написать число, равное сумме его цифр?

12. Найдите значение выражений 29 • 11, 37 • 11, 47 • 11, 85 • 11, 97 • 11.
Верно ли: чтобы найти результат умножения двузначного числа на 11 в случае, когда сумма цифр двузначного числа больше или равна 10, достаточно между цифрой десятков, увеличенной на 1, и цифрой еди­ниц написать число, равное разности между суммой его цифр и чис­лом 10?

13. На множестве выражений, приведенных ниже, задано отноше­ние «содержать в произведении цифру 0». Определяет ли оно разбие­ние этого множества на классы? Если да, то выполните его, не вычис­ляя произведений.

2602•3 1803•6 17009•4

2602•7 1803•2 17019•4

26002•8 18003•7 17019•7.

Алгоритм деления

Когда речь идет о технике деления чисел, то этот процесс рассматривают как действие деления с остатком: разделить целое неотрицательное число а на натуральное число b — это значит найти такие целые неотрицательные числа q и r, что a = bq + r, причем 0≤ r b и число разрядов в числах а и b одинаково, то частное q находим перебором, последовательно умножая b на 3, 4, 5, 6, 7, 8, 9, так как а b и число разрядов в числе а больше, чем в чис­ле b, то записываем делимое а и справа от него делитель b, который отделяем от а уголком и ведем поиск частного и остатка в такой последовательности:

a) Выделяем в числе а столько старших разрядов, сколько разрядов в числе b или, если необходимо, на один разряд больше, но так, чтобы они образовывали число d₁, больше или равное b. Перебором находим частное q₁, чисел d₁, и b, последовательно умножая b на 1, 2, 3, 4, 5, 6, 7, 8, 9. Записываем q₁ под уголком (ниже b).

б) Умножаем b на q₁, и записываем произведение под числом a так, чтобы младший разряд числа bq₁, был написан под ним разрядом выделенного числа d₁.

в) Проводим черту под bq₁ и находим разность r₁ = d₁ — bq₁.

г) Записываем разность r₁ под числом bq_1, приписываем справа к r₁ старший разряд из неиспользованных разрядов делимого а и сравниваем полученное число d₂ с числом b.

д) Если полученное число d₂ больше или равно b, то относительно него поступаем согласно п. 1 или п. 2. Частное q₂ записываем после q ₁ .

е) Если полученное число d₂ меньше b, то приписываем еще столько следующих разрядов, сколько необходимо, чтобы получить первое число d₃, большее или равное b. В этом случае записываем после q₁ такое же число нулей. Затем относительно d₃ поступаем согласно пп. 1, 2. Частное q₂ записываем после нулей. Если при использовании младшего разряда числа а окажется, что d₃ или

Источник

Читайте также:  Способы прекращения юридических лиц без универсального правопреемства