Назовите способы образования поверхностей

Назовите способы образования поверхностей

Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б

Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.

Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.

В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.

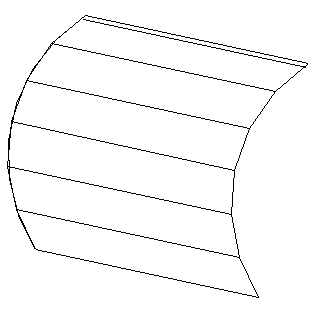
Рисунок 37

На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.

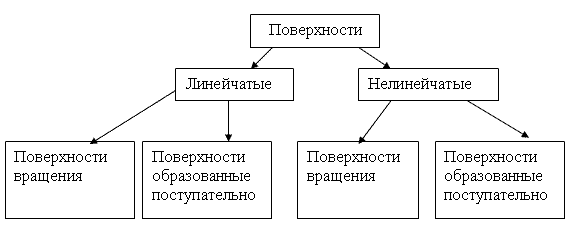
Рисунок 38

Линейчатые поверхности вращения – это конус, цилиндр.

Линейчатые поверхности поступательного движения – все гранные поверхности.

К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.

Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.

Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.

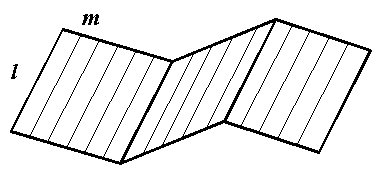
Рисунок 39

Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.

Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.

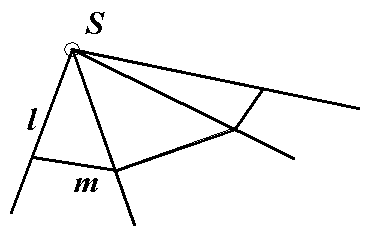
Рисунок 40

Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.

1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?

2. Назовите линейчатые поверхности вращения.

3. Какие нелинейчатые поверхности вы знаете?

4.Какая линия является направляющей у гранных поверхностей, какая является образующей?

5. Как образуется поверхность пирамиды, призмы?

6. Какая призма называется прямой?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Назовите способы образования поверхностей

Контрольные задания по теме:
Рабочая тетрадь задача 58а, задача 58б

Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.

Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.

В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.

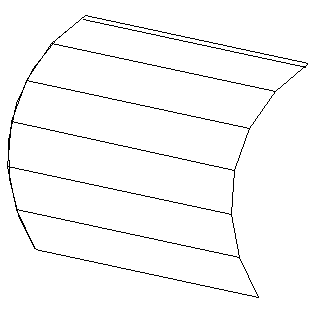
Рисунок 37

На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.

Рисунок 38

Линейчатые поверхности вращения – это конус, цилиндр.

Линейчатые поверхности поступательного движения – все гранные поверхности.

К нелинейчатым поверхностям вращения относятся сфера, шар, эллипсоид. Нелинейчатые поверхности, образованные поступательным движением – это гиперболический параболоид и другие сложные поверхности.

Образующей является прямая линия, направляющая – ломаная. Гранная поверхность представляет из себя совокупность пересекающихся плоскостей – граней. Линии пересечения граней – ребра. Точки пересечения ребер – вершины.

Наиболее простой является призматическая поверхность. Она изображена на рисунке 39. Образующая l передвигается вдоль ломаной линии m, которая является направляющей. Все образующие поверхности параллельны.

Рисунок 39

Призмой называется геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которое получается, если призматическую поверхность ограничить двумя основаниями. Основания будут иметь форму многоугольников, боковые грани параллелограммов. Если плоскости основания перпендикулярны боковым граням, то призма называется прямой, если нет то наклонной. Если в основании призмы лежит правильный многоугольник, то призма называется правильной.

Пирамидальная поверхность изображена на рисунке 40. Один конец образующей l неподвижен, а другой передвигается вдоль ломаной линии m.

Рисунок 40

Пирамидой является геометрическое тело, образующееся при ограничении призматической поверхности плоскостью, которая будет называться основанием. Точка S-вершина пирамиды. Боковые грани – треугольники. Пирамида будет называться правильной, если в основании лежит правильный многоугольник, а высота опущенная из вершины попадает в центр основания.

1. Что называется поверхностью? Какие способы образования поверхностей вы знаете?

2. Назовите линейчатые поверхности вращения.

3. Какие нелинейчатые поверхности вы знаете?

4.Какая линия является направляющей у гранных поверхностей, какая является образующей?

5. Как образуется поверхность пирамиды, призмы?

6. Какая призма называется прямой?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Способы образования поверхностей

Образование поверхностей. Классификация поверхностей. Гранные поверхности. Сечение гранных поверхностей плоскостями. Построение разверток призмы, пирамиды

Мир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения.

Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией.

В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим.

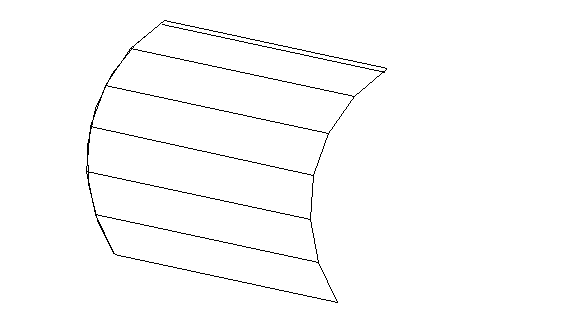На рисунке 37 прямая линия — образующая, а дуга, вдоль которой она перемещается, — направляющая. Другим способом образования поверхности и задания ее на чертеже является задание множества принадлежащих ей точек и линий. Такой способ называется каркасным, а упорядоченное множество точек и линий поверхности называется ее каркасом.

Источник

Способы образования поверхностей

Существует два наиболее распространенных способа образования поверхностей: 1) при помощи движущейся линии; 2) при помощи движущейся поверхности. Рассмотрим указанные способы.

1. Пусть некоторая линия s (называемая образующей поверхности) непрерывно перемещается в пространстве, занимая последовательно положения s₁, s₂, . s_i , . ,s_n (рис.9.1). При движении линия может быть неизменной или непрерывно менять свою форму. Каждая точка A_j, принадлежащая линии s, при своем перемещении опишет некоторую траекторию t_j. Линии t, называются направляющими, так как их можно рассматривать как линии, по которым перемещается образующая s. Совокупность линий s_i и t_j образует каркас поверхностиили сеть. Данный способ образования поверхностей называется кинематическим и является основным в начертательной геометрии. Он широко используется в технике. Например, так происходит формообразование поверхностей при обработке деталей на металлорежущих станках с линейным контактом режущего инструмента (резца, фрезы и т.п.) и заготовки. В этом случае поверхность детали несет на себе «отпечаток» профиля инструмента. Поверхности, образованные таким способом, называются кинематическими.

Рис.9.1

2. В этом случае некоторая поверхность F (называемая производящей поверхностью) перемещается в пространстве, занимая ряд последовательных положений F₁, F₂, …, F_n. Совокупность всех положений поверхности F определяет некоторую новую поверхность Φ, являющуюся огибающей этих поверхностей. Огибающая поверхность может касаться производящей поверхности по некоторой линии (например, ковш обычного или роторного экскаватора при рытье траншей, каналов, проходке тоннелей) или в точке (обработка некоторой выпуклой поверхности торцом сферической или пальцевой фрезы).

Кроме этих двух наиболее распространенных способов образования поверхностей в научных исследованиях по начертательной и прикладной геометрии применяются еще некоторые другие способы, такие, например, как способ конкурирующих поверхностей, способ мгновенных преобразований.

Суть способа конкурирующих поверхностейзаключается в следующем. Пусть в пространстве заданы две конкурирующие поверхности, проекции которых на одну из плоскостей проекций совпадают всеми своими точками. Тогда две оставшиеся не совпавшие проекции (по одной от каждой поверхности) определяют новую поверхность. Этот способ является обобщением так называемых «ключевых» способов образования поверхности, когда искомая поверхность конструируется графически без применения аналитических расчетов.

Способ мгновенных преобразований, в отличие от предыдущего способа, является аналитическим. Он связан с заданием в пространстве некоторого преобразования Т, определяемого уравнениями:

где t — переменный параметр.

Придавая параметру различные непрерывные значения, можно получить непрерывное множество преобразований T₁, T₂. T_j, зависящих от параметра t. Каждое отдельно взятое преобразование T_j, соответствующее значению параметра t_j, называется мгновенным преобразованием. Такое однопараметрическое множество размножает точку пространства в линию, линию пространства в поверхность, поэтому способ применяется для образования поверхностей. Совокупность аналитического выражения исходной образующей линии (если она задана математически) и преобразований дает уравнение непрерывного каркаса сконструированной поверхности (о каркасе поверхности более подробно ниже).

Дата добавления: 2014-12-18 ; просмотров: 861 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник