Найти значение разности разными способами 2 класс

Математика 2 класс учебник Петерсон 1 часть — страница 28

• Тип: ГДЗ, Решебник.
• Автор: Л. Г. Петерсон.
• Год: 2021.
• Серия: Учись Учиться.
• Издательство: Просвещение/Бином.

Подготовили готовое домашнее задание к упражнениям на 28 странице по предмету математика за 2 класс. Ответы на задания: 1, 2, 3, 4, 5 и 6.

Учебник 1 часть — Страница 28.

Ответы 2021 года.

15 УРОК

Повторяются приемы сложения и вычитания двузначных чисел с переходом через разряд, а с другой – наблюдаем взаимосвязь между компонентами и результатами сложения и вычитания, которая позволяет упростить вычисления.

Так, в первом столбике можно вычислить значения сумм либо три раза, либо всего лишь один, если заметить, что одно слагаемое не изменяется, а второе увеличивается на 1. Значит, сумма тоже будет увеличиваться на 1. Поэтому, вычислив значение суммы 29 + 62 = 91, остальные значения получаем сразу: 92, 93.

Аналогично во втором столбике уменьшаемое увеличивается на 1, а вычитаемое не изменяется. Значит, разность тоже будет увеличиваться на 1. Поскольку 90 – 64 = 26, то остальные значения разностей получаем, не вычисляя: 27, 28.

В третьем столбике уменьшаемое не изменяется, а вычитаемое увеличивается на 1. Значит, разность будет, наоборот, уменьшаться на 1. Значение первой разности 54 – 16 = 38, поэтому остальные значения разностей: 34, 36.

29 + 62 = 91 90 – 64 = 26 54 – 16 = 38
29 + 63 = 92 91 – 64 = 27 54 – 17 = 37
29 + 64 = 93 92 – 64 = 28 54 – 18 = 36

а b – 5
4 > d – d так как d – d = 0

a + b = b + a от перестановки слагаемых
значение суммы не меняется.
k + 26 54 – n но если n = 0, то 54 + n = 54 – n

38 – b c – 90 так как 19 > 90
a – 0 = a + 0

Объясни приём вычислений: 73 – 19 = 74 – 20 = 54.
Вычисли, используя этот приём.

73 – 19 = 74 – 20 = 54 Если уменьшаемое и вычитаемое увеличить на одинаковое количество единиц, то разность не изменится.

35 – 9 = 36 – 10 = 26
62 – 18 = 64 – 20 = 44
91 – 37= 94 – 40 = 54
54 – 29 = 55 – 30 = 25

а) В ателье приняли заказ на пошив 37 юбок, а платьев – на 2 меньше, чем юбок. Сколько всего платьев и юбок должно сшить ателье по этому заказу?
б) В магазине продали за час 29 кукол, что на 2 меньше, чем продали за это же время медведей. Сколько всего кукол и медведей продали за этот час?

а) Оформить задачу можно по-разному:

– Чтобы узнать, сколько всего платьев и юбок должно сшить ателье, надо сложить количество платьев и юбок. (Ищем целое.) Количество юбок известно – 37. Количество платьев не известно, но сказано, что их было на 2 меньше, чем юбок.
Значит, мы можем его найти, уменьшив 37 на 2. Затем сложим полученное число с 37 и ответим на вопрос задачи.

1) 37 – 2 = 35 (шт.) – заказали платьев.
2) 37 + 35 = 72 (шт.)
Ответ: должно сшить всего 72 платья и юбок.

б) Оформить задачу можно по-разному:

– Чтобы узнать, сколько всего кукол и медведей продали за час, надо сложить их количество. (Ищем целое.) Известно, что за час продали 29 кукол. Количество проданных медведей не известно, но сказано, что их было на 2 больше, чем кукол. Значит, мы можем его найти, увеличив 29 на 2. Затем сложим полученное число с 29 и ответим на вопрос задачи.

1) 29 + 2 = 31 (шт.) – продали медведей.
2) 29 + 31 = 60 (шт.)
Ответ: за час продали 60 кукол и медведей.

Вспомним:
Сравнивать, складывать и вычитать величины можно только тогда, когда они выражены в одних и тех же единицах измерения.
1 дм = 10 см

3 дм 7 см + 4 дм 5 см = 37 см + 45 см = 82 = 8 дм 2 см

7 дм 2 см – 56 см = 72 см – 56 см = 16 см = 1 дм 6 см

26 см + 3 дм 8 см = 26 см + 38 см = 64 см = 6 дм 4 см

6 дм 8 см – 9 см = 68 см – 9 см = 59 см = 5 дм 9 см

Вставь в квадраты пропущенные цифры:

Рейтинг

Источник

Как найти разность чисел в математике

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

Каждый результат этих действий также имеет своё название:

• сумма — результат, получившийся при сложении чисел;
• разность — результат, получившийся при вычитании чисел;
• произведение — результат умножения чисел;
• частное — результат деления.

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

• сумма — прибавить;
• разность — отнять;
• произведение — умножить;
• частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

• Разность чисел означает, насколько одно из них больше другого.
• Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
• Это вычитание одного числа из другого.
• Это цифра, составляющая остаток при минусовании двух величин.
• Это величина, являющаяся результатом вычитания двух значений.
• Разность показывает количественное различие между двумя цифрами.
• Это результат одного из четырёх арифметических действий, которым является вычитание.
• Это то, что получится, если из уменьшаемого отнять вычитаемое.

Видео: Математика 6 Делимость суммы и разности чисел

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

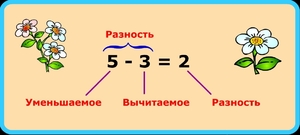
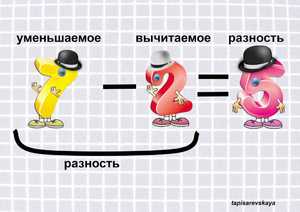
• Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

• Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

• Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
• Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Видео: Математика 2 класс. Разность двухзначных чисел

Простые примеры

• Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

• Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

• Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

• Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);

Ответ: 40 — разница трёх значений.

• Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

• Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

• Удвоенное число — это величина, умноженная на два.
• Утроенное число — это величина, умноженная на три.
• Удвоенная разность — это разница величин, умноженная на два.
• Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

• Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина;

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

• Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

• сумму — сложением слагаемых;
• произведение — умножением множителей;
• частное — делением делимого на делитель.

Источник

Как найти разность чисел в математике

Содержание:

Само слово «разность» мы часто употребляем в нашей повседневной речи, объясняя им различие чего либо. Например, говоря о различии разных мнений и взглядов можно сказать о «разности» в них. Часто этот термин употребляется в науках, им обозначают разные количественные показатели, скажем разность электрических потенциалов, атмосферного давления или количества сахара в крови человека. Но прежде всего «разность» – это математический термин и об этой его ипостаси мы поговорим в нашей статье.

Арифметические действия с числами

Все основные арифметические действия с числами делятся на четыре большие группы:

Результат каждого из этих действий в свою очередь имеет свое уникальное название:

• сумма – результат от сложения чисел или говоря простым языком – сума, когда мы прибавляем,
• разность – результат от вычитания чисел или – когда мы отнимаем,
• произведение – результат от умножения чисел,
• частное – результат от деления чисел.

Роль в математике

Исходя из выше написанного, несложно дать определение того, что такое разность чисел, причем это понятие можно обозначить сразу несколькими способами:

• Разность между числами показывает нам, насколько одно число является больше другого.
• Разностью также называют итог, который получился при отнимании друг от друга двух или больше чисел.
• Разность двух чисел – вычитание одного числа от другого.
• Разность – цифра, составляющая остаток при минусовании двух величин.
• Она показывает количественное различие между цифрами.

Все эти определение разности являются правильными.

Как найти разность величин

Разность – это результат вычитания одного числа из другого. Первое из этих чисел, с которого делается вычитание, называют уменьшаемым, а второе число называется вычитаемым, его как раз вычитают из первого числа. Итак, чтобы найти значение разности чисел нужно просто от уменьшаемого отнять вычитаемое.

Тут все предельно просто, но при этом у нас появилось еще два дополнительных термина, которые также надо знать:

• Уменьшаемое – математическое число, от которого отнимают, в результате оно уменьшается.
• Вычитаемое – это то математическое число, которое вычитают от уменьшаемого.

Итого, для того, чтобы найти разность необходимо знать значение уменьшаемого и вычитаемого, они должны быть известны.

Порой необходимо решить задачу обратную, при известной разности найти уменьшаемое или вычитаемое число. Сделать это тоже просто:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Примеры нахождения

Пример 1. Найти разницу двух величин.
Дано: 20 — уменьшаемое, 15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.
Дано: 48 — разность, 32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.

Пример 3. Найти вычитаемое значение.
Дано: 7 — разность, 17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: 10.

И немного более сложных примеров, ведь в математике зачастую высчитывают разность с использованием не только двух, но и гораздо большего количества компонентов, в которых могут быть к тому же не только лишь целые числа, но и дробные, рациональные, иррациональные числа.

Пример 4. Найти разницу трех значений.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение, 12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми);
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трех значений.

Пример 5. Найти разницу величин 7 и 18.
Дано: 7 — уменьшаемое значение, 18 — вычитаемое.
Вроде все просто, но ведь вычитаемое у нас больше уменьшаемого, как быть в таком случае? В таком случае действует следующее правило: если вычитаемое больше уменьшаемого, то разность окажется отрицательной или другими словами, она будет числом со знаком минус.
Решение: 7 — 18 = —11
Ответ: —11 — отрицательное число со знаком минус.

Источник