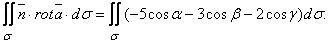Найти циркуляцию векторного поля по контуру двумя способами

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 12.14 Найти модуль циркуляции векторного поля 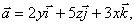&nbsp &nbsp
вдоль контура
&nbsp &nbsp

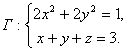
Решение

&nbsp &nbsp &nbsp &nbsp Согласно формуле Стокса:

.
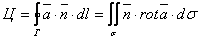
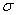
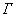
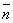
&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — участок поверхности, ограниченный контуром &nbsp &nbsp &nbsp &nbsp , &nbsp &nbsp &nbsp &nbsp — единичный вектор нормали к данной поверхности.

&nbsp &nbsp &nbsp &nbsp Найдём ротор векторного поля

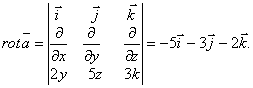
&nbsp &nbsp &nbsp &nbsp Тогда интеграл запишется

&nbsp &nbsp &nbsp &nbsp Здесь &nbsp &nbsp &nbsp &nbsp — направляющие косинусы нормали к поверхности или координаты единичного вектора нормали.
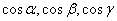
&nbsp &nbsp &nbsp &nbsp Из общего уравнения плоскости запишем координаты нормального вектора 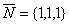&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Находим длину нормального вектора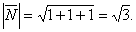
.
&nbsp &nbsp &nbsp &nbsp Тогда направляющие косинусы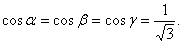
.

&nbsp &nbsp &nbsp &nbsp Элемент поверхности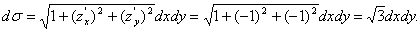
.

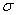
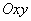
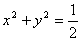
&nbsp &nbsp &nbsp &nbsp Проекцией поверхности &nbsp &nbsp &nbsp &nbsp на плоскость &nbsp &nbsp &nbsp &nbsp является круг

&nbsp &nbsp &nbsp &nbsp Этот круг имеет центр в начале координат и радиус 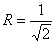&nbsp &nbsp &nbsp &nbsp.

&nbsp &nbsp &nbsp &nbsp Площадь данного круга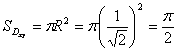
.
&nbsp &nbsp &nbsp &nbsp Переходя от поверхностного интеграла к двойному, получим

&nbsp &nbsp &nbsp &nbsp Тогда модуль циркуляции 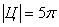&nbsp &nbsp &nbsp .
&nbsp &nbsp &nbsp &nbsp Ответ: Модуль циркуляции равен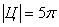&nbsp &nbsp &nbsp .

Источник

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $\overline=(3x-y) \overline+(6z+5x) \overline$

Задача 4. Вычислить потенциальную функцию векторного поля

Поток поля через поверхность

Циркуляция векторного поля

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ \overline = (3x-1) \overline+ (y-x+z)\overline+4z \overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $\overline = xz \overline -\overline+y \overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y \ge 0)$ от точки $M(\sqrt(3);0;1)$ до точки $N(-\sqrt(3);0;1)$.

Читайте также: Способы формирования положительного отношения
Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ \overline = z \overline+ (x+y)\overline+y \overline, \quad (p): 2x+y+2z=2. $$

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.

Источник