Найти сумму чисел от 1 до 10 2 способами

Вычисли удобным способом значение суммы чисел от 1 до 10

Ответ или решение 2

В предложенном задании нас просят вычислить удобным способом сумму чисел от 1 до 10 включительно. Для простого решения данной и подобных заданий существует специальный способ.

Способ вычисления суммы чисел в промежутке

• Для решения подобного рода задач необходимо составить максимальное количество пар, которые в сумме дают одно и то же число, плюс само это число, которое, как правило, является последним в промежутке.
• Затем умножить количество этих пар плюс ещё один (само число) на число, которое они дают в сумме.
• Теперь осталось прибавить число из середины промежутка, которое осталось без пары. Так мы легко и максимально быстро получим правильный ответ.

Рассмотрим на примере промежутка от 1 до 100

• Составим максимальное количество пар, которые в сумме дают одно и тоже число. Такими парами будут 1 и 99, 2 и 98, 3 и 97, 4 и 96 и так далее до пары 49 и 51. В сумме они дают 100. Таких пар всего будет 49 (потому что на 49 мы остановились), плюс само число 100, на которое оканчивается промежуток, то есть получается 50 пар по сто.
• Умножаем количество пар, то есть 50 на саму их сумму, то есть также на 100:

• Теперь осталось только прибавить число 50, которое не имеет пару и поэтому не было посчитано:

• Всё, так мы нашли сумму всех цифр от 1 до 100 включительно.

Наконец, используя данный метод вычисления, можем выполнить предложенное задание.

Сумма цифр от 1 до 10

• В данном примере пары будут такими: 1 и 9, 2 и 8, 3 и 7, 4 и 6, которое дают в сумме 10, плюс само число 10.
• Теперь умножаем количество пар, то есть 5 на их сумму, то есть на 10:

• Осталось только прибавить число 5, которое не имело пары:

У данной задачи есть как минимум два решения. Первый самый простой, но не совсем удобный. Для этого просто нужно сложить весь цифрой ряд от 1 до 10 между собой.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55:

Но есть способ немного проще и быстрее. В ряду от от единицы до десяти находится 10 цифр, если разложить их двумя рядами, то и сложить, то можно увидеть закономерность.

То есть если числовой ряд кратен двум и не прерывается, то достаточно сложить сложить первую и последнюю цифру в числовом ряду и умножить ее на половину количества цифр в числовом ряду.

Источник

Найти сумму чисел от 1 до 10

1 Найти сумму чисел от 1 до 10
2 Найти сумму четный чисел от 1 до 10
3 Найти сумму нечетных чисел от 1 до 10
4 Найти произведение чисел от 1 до 10
5 Найти произведение четных чисел от 1 до 10
6 Найти произведение нечетных от 1 до 10
7 Найти сумму чисел от 1 до n
8 найти сумму четных чисел от 1 до n
9 найти сумму нечетных чисел от 1 до n
10 найти произведение чисел от 1 до n
11 найти произведение четных чисел от 1 до n
12 найти произведение нечетных от 1 до n
13 найти сумму четных и произведение нечетных чисел от 1 до n

14 Найти сумму отрицательных элементов массива состоящего из 20 целых элементов заданного случайным образом в диапазоне от -20 до 10. а также найти кол-во этих элементов.

15 задан массив из 10 целых элементов,заданного случайным образом в диапазоне от -10 до 10. Найти максимальный и минимальный элементы массива. Найти произведение макс и мин элементов массива.

16 задан массив состоящий из 15 целых элементов заданного случайным образом в диапазоне от -10 до 10 отсортировать элементы массива по возрастания.

Или объясните как их решать

Дана последовательность из n-чисел.Найти сумму всех чисел,начиная с 5-го числа и вычислить сумму первых 4-х чисел.
Дана последовательность из n-чисел.Найти сумму всех чисел,начиная с 5-го числа и вычислить сумму.

С клавиатуры вводится N целых чисел a1, a2,….,aN. Найти сумму этих чисел. Найти номер первого четного числа последовательности чисел.
Решить задачу 3 способами: 1. Используя метки и оператор goto (не используя никакой цикл) 2.

Найти сумму квадратов чётных чисел и сумму кубов нечётных чисел от 1 до Н
Даны 2 задания , 1) найти сумму квадратов чётных чисел и сумму кубов нечётных чисел от 1 до Н .

Если последняя цифра первого числа чётная то найти сумму чисел, иначе найти произведение последних цифр чисел
Дано два двузначных числа. Если последняя цифра первого числа четная то найти сумму исходных чисел.

Источник

Сумма от 1 до 10 через while

Сумма денег S в банке под процентом T. Какая будет сумма через 1, 2, 3, 4, 5 лет?
Помогите((( сума денег S в банку под процентом T. Какая будет сума через 1, 2, 3, 4, 5, лет?

На счет в банке положена денежная сумма под процент. Какая сумма будет на счете через 5 лет?
На счет в банке на 5 лет была положена определенная денежная сумма под определенный годовой.

Под какой процент была вложена сумма x рублей, если через n лет сумма наращенного капитала составила y рублей?
Заранее спасибо.

Решение

Сумма ряда через for
Помогите исправить ошибки к задаче. Вычислить значение суммы S = 1×2 + 2×3×4 +.

Сумма чисел через for
Здравствуйте можете показать 1 из способов сложение двух чисел через программирование цикл for.

Сумма ряда через цикл while
Как правильно написать программу с циклом while? Попыталась решить вторую последовательность, но.

Сумма из цифр через пробелы
Есть задача: «В текстовое поле вводится строка из трех цифр, разделенных пробелами. При нажатии.

Сумма цифр через рекурсию
Найти сумму всех цифр введённого числа через рекурсию.

Сумма Гаусса n элементов через while
Вот написала 2 способа для вычисления суммы элементов по формуле суммы Гаусса. Ошибок не выдает.

Сумма диапазона через макрос
Здравствуйте, помогите, пожалуйста, написать макрос, который будет считать сумму значений ячеек в.

Источник

Сумма чисел от 0 до 10.

Вычислить разность между S1 и S2, где S1-сумма четных чисел от I1 до I2, S2-сумма четных чисел от J1 до J2.
Помогите пожалуйста написать вот такую программу: Вычислить разность между S1 и S2, где S1-сумма.

Найти индекс элемента, сумма чисел идущих до него минус сумма чисел идущих после него будет минимальной
Дан динамеческий массив. Найти индекс элемента, сумма чисел идущих до него минус сумма чисел.

Сумма всех натуральных чисел от 1 до 1000, сумма цифр которых равна 10
Я сначала хотел написать рекурсивную функцию, которая сводила бы расчёт от 3-охзначных чисел к.

Запросить 100 четвёрок чисел, сосчитать число четвёрок, где сумма 1 числа больше чем сумма 2 и 3
задача решить на паскале двумя способами 1), Через function. 2). procedura Начиная в Вар, Бегин. .

Вычислить произведение P кубов трех чисел a, b и c, если их сумма меньше нуля, произведение P модулей трех чисел a, b и c, если их сумма больше нуля
Вычислить произведение P кубов трех чисел a, b и c, если их сумма меньше нуля, произведение P.

Найти все пары чисел а и b такие, что сумма чисел равна х
Задание:Требуется написать программу которая по заданным числам х и y найдет все пары чисел а и b.

Если сумма двух чисел меньше 1, то большее из чисел заменить их произведением
помогите решить в С++. Если сумма двух действительных чисел x и y меньше 1, то большее из чисел x и.

Определить номер строки массива натуральных чисел, сумма чисел которой наибольшая
Сформировать массив натуральных чисел с M рядков и N столбцов.Определить номер рядка, сумма чисел.

Вычислить 2 числа из 2-х диапазонов чисел, сумма этих чисел равна заданному числу
Здравствуйте, уважаемые форумчане. Помогите, пожалуйста, с пониманием алгоритма написания этой.

Источник

Занимательная математика: правило Гаусса

Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.

Первая статья из этого цикла посвящена правилу Гаусса.

Немного истории

Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.

Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:

Найти сумму всех натуральных чисел от 1 до 100.

Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.

Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.

Гаусс сгруппировал числа следующим образом:

(1+10) + (2+9) + (3+8) + (4+7) + (5+6)

Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо

Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:

1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100

Находим количество пар в ряде натуральных чисел. В данном случае их 50.

Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.

Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050

Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.

Задачи на использование правила Гаусса

А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.

Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.

В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.

Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.

Задача 1

Найти сумму чисел:

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
• 1 + 2 + 3 + … + 14 + 15 + 16;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.

Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
• 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
• 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050

Задача 2

Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?

С помощью правила Гаусса находим сумму всех весов:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)

Далее смотрим, можно ли этот вес разбить на три равных веса:

Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.

Один из вариантов:

Другие возможные варианты найдите сами с ребенком.

Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).

Задача 3

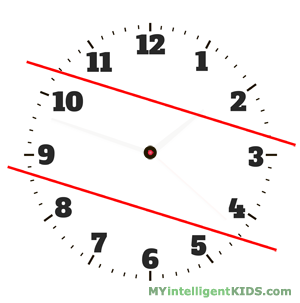
Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

Значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.

Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.

Задача 4

Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?

Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78

78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.

По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:

1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.

Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.

Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.

Задача 5

Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?

Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:

1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.

Задача 6

Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?

Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:

• первая клетка — 1,
• вторая — 2,
• третья — 3,
• …
• восьмая — 8,
• девятая — 9.

Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.

Задача 7

Вычислить сумму, используя прием Гаусса:

• 31 + 32 + 33 + … + 40;
• 5 + 10 + 15 + 20 + … + 100;
• 91 + 81 + … + 21 + 11 + 1;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
• 1 + 2 + 3 + 4 + 5 + 6;
• 4 + 6 + 8 + 10 + 12 + 14;
• 4 + 6 + 8 + 10 + 12;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.

• 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
• 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
• 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
• 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
• 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
• 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
• 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.

Задача 8

Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?

Применяем правило Гаусса, чтобы найти общую массу гирек:

1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)

Вычисляем массу гирек, которые убрали:

Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.

Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.

Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):

1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.

Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.

Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.

Источник