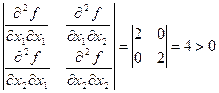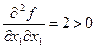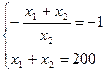Найти оптимальный способ реализации

Анализ оптимального плана симплекс-таблицы

Решение находим с помощью калькулятора. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 3x₁ + 2x₂ при следующих условиях-ограничений.
x₁ + 2x₂ 0 в столбце x2 означает, что использование x₂ — не выгодно. Значение 3 в столбце x₄ означает, что теневая цена (двойственная оценка) равна 3.

Пример . Фирме «Иерихонская сталь» предстоит решить, какое количество чистой стали, и какое количество металлолома следует использовать для приготовления (из соответствующего сплава) литья для одного из своих заказчиков. Пусть производственные затраты в расчете на 1т чистой стали равняются 3 у.е., а затраты в расчете на 1 т металлолома – 5у.е. (последнее число больше предыдущего, т.к. использование металлолома сопряжено с его предварительной очисткой). Заказ предусматривает поставку не менее 5 т литья; при этом заказчик готов купить большее количество литья, если фирма «Иерихонская сталь» поставит перед ним такие условия.
Предположим, что запасы чистой стали, ограничены и не превышают 4 т, а запасы металлолома не превышают 6 т. Отношение веса металлолома к весу чистой стали в процессе получения сплава не должно превышать 7:8. Производственно – технологические условия таковы, что на процессы плавки и литья не может быть отведено более 18 часов, при этом на 1 т стали уходит 3 часа, а на 1 т металлолома – 2 часа производственного времени.
Постройте линейную оптимизационную модель.

x₁ — чистая сталь, [т], x₂ — металлолом, [т]

Ограничения по структуре:
x₁ : x₂ ≤ 7:8

Ограничения по ресурсам:
3x₁ + 2x₂ ≤ 18

Ограничения по поставкам:
x₁ + x₂ ≥ 5

Источник

Пример 4.4.1

Расчет экономико-математической модели при нелинейных затратах на производство

Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции.

Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации автомобилей через магазин расходы на реализацию составляют усл. ед., а при продаже автомобилей через торговых агентов расходы составляют усл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 штук.

Составим математическую модель задачи.

Целью является минимизация суммарных расходов

.

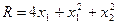
Управляющие переменные – это число автомобилей, реализуемых первым и вторым способом: и соответственно (200 штук). Окончательно математическая модель имеет следующий вид:

.

.

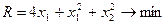
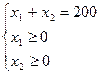
Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид

.

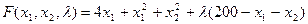
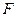
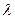
Найдем частные производные функции по , и и приравняем их к нулю.

Получим следующую систему уравнений:

.

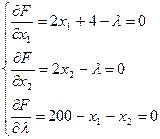
Решая систему, найдем

=99, =101, =202, =20398.

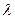
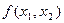
Определитель, составленный из вторых частных производных функций 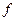по , , имеет вид

Следовательно, по теореме о достаточном условии существования условного экстремума функция 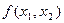в точке =99, =101 действительно имеет экстремум.

следовательно в этой точке функция 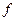имеет условный минимум.

Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20398 усл. ед.

Данную задачу можно было решить и графическим методом (рис. 4.4.1).

Рис. 4.4.1

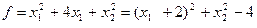
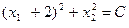
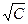
Областью допустимых решений задачи является отрезок АВ, линиями уровня функции являются концентрические окружности с центром в точке =-2, =0 и радиусом .

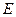
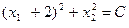
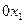
Из рисунка видно, что минимальное значение функции, принадлежащее области допустимых решений, достигается в точке , в которой совпадают угловой коэффициент прямой =200-и касательной к окружности к оси .

Продифференцировав последнее уравнение по , получим

,

.

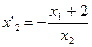
Приравняем последнее выражение к угловому коэффициенту прямой и добавим к этому уравнению уравнение прямой, которой принадлежит точка Е.

Решив последнюю систему, найдем оптимальные значения: =99, =101, =20398.

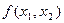
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Подробный разбор симплекс-метода

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

• Если , то
• Если — любой, то , где

Замечание: Будем нумеровать по номеру неравенства, в которое мы его добавили.

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m

Источник