Задача № 5
По заданным в таблице координатам построить наглядное изображение и эпюр точки. Для каждой точки построить отдельный чертеж. Ось оу проводим под углом 45 0 к горизонтали и откладываем на ней размеры в 2 раза меньше заданного в таблице размера. При построении ортогональных проекций точек размеры откладываем в натуральную величину.
| 1. А | 2. В | 3. С | 4.Д | ||||||||||||
| № | х | у | z | № | х | у | z | № | х | у | z | № | х | у | z |
Задача № 6* и образец ее решения.
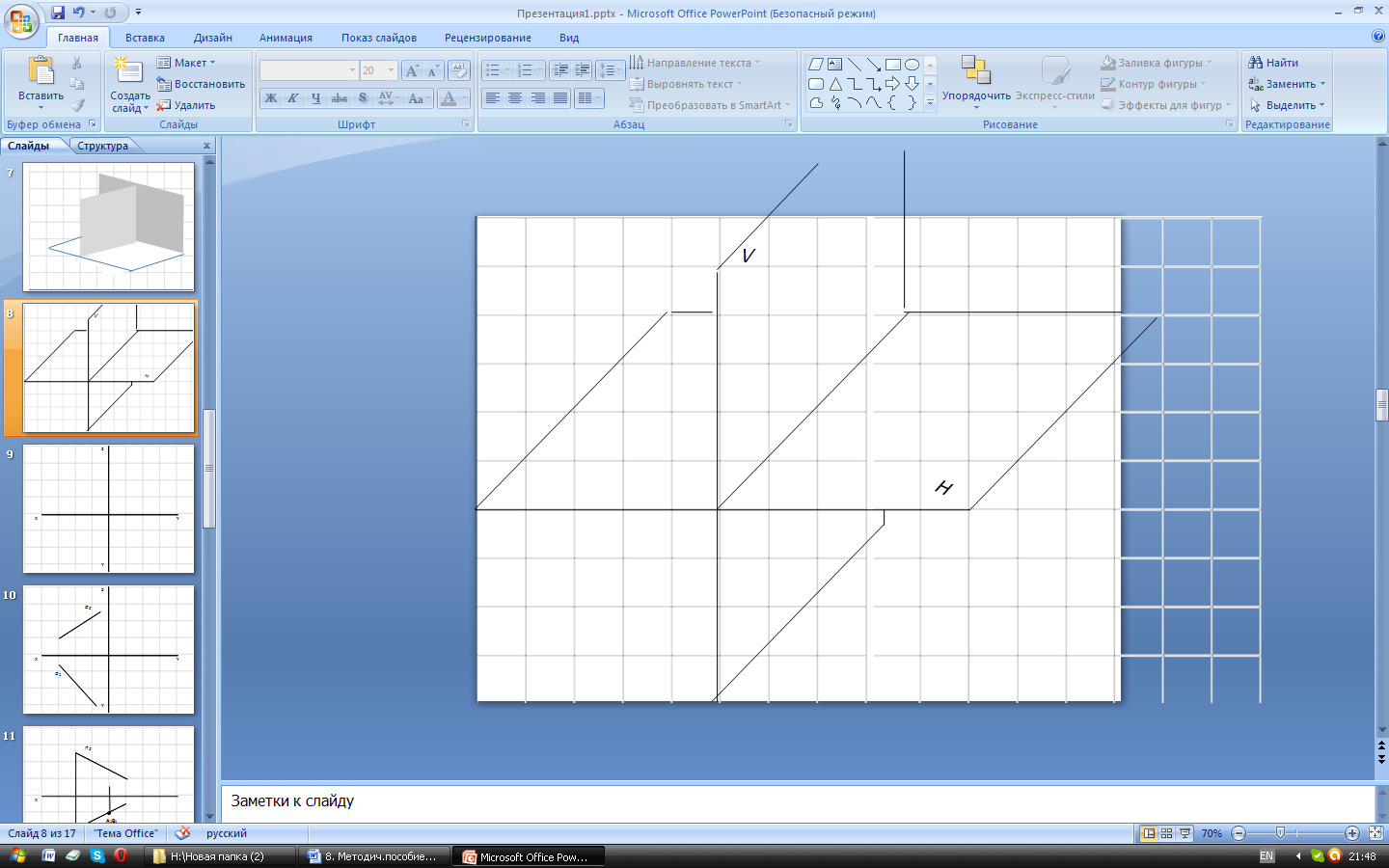
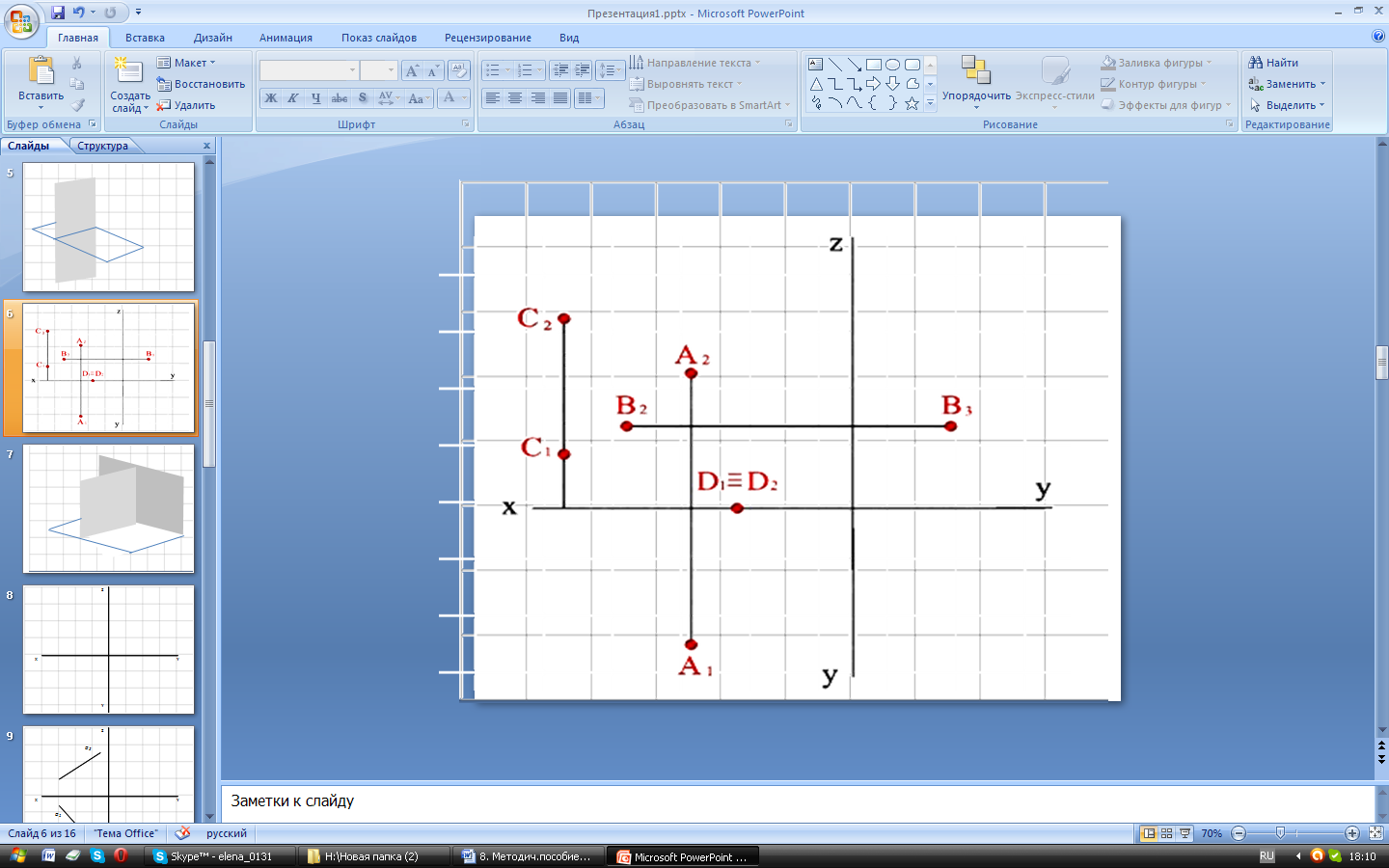
Дать наглядные изображения точек А, В, С, D Относительно плоскостей V и H. Точки заданы своими проекциями (рис. а).
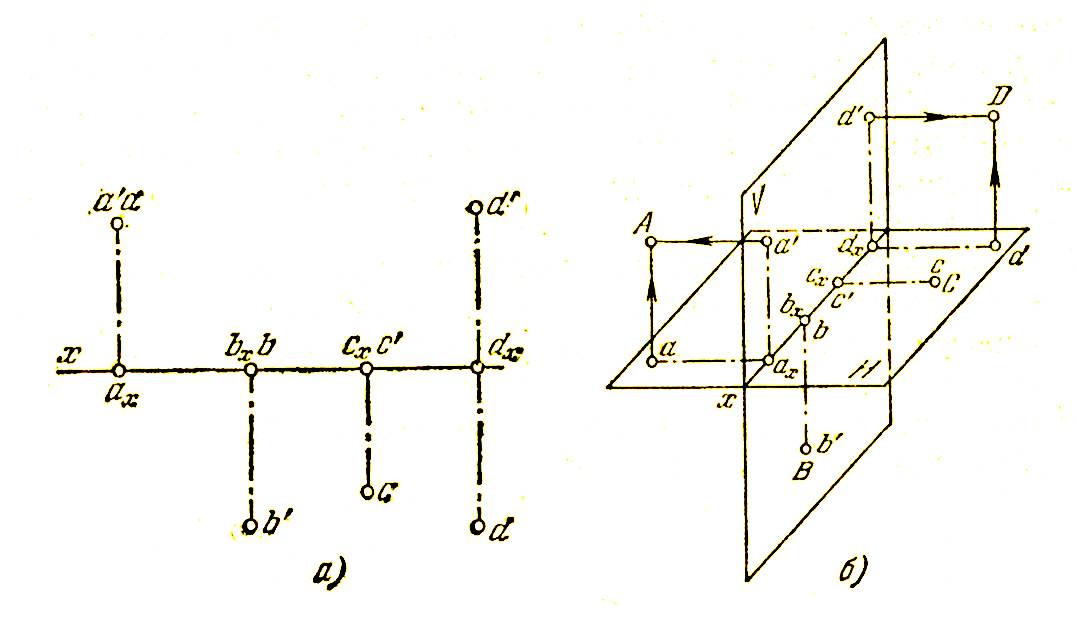 |
Решение: Точки ах, вх, сх, dх ( рис. б) выбираем на оси х произвольно. Так как точка А находится во второй четверти (аппликата точки положительна, ордината отрицательна), то отрезок аха, соответствующий значению ординаты откладываем влево от плоскости V . Отрезок аха‘, соответствующий значению аппликаты, откладываем вверх от плоскости Н.
Для построения точки D, находящейся в первой четверти (аппликата и ордината положительны), отрезок dxd откладываем влево от плоскости, а отрезок dxd’ – вверх от плоскости Н.
Положения точек А и D, получены на пересечении перпендикуляров, проведенных через точки а и d к плоскости Ни через точки а’ и d’ к плоскости V.
Точка В лежит в плоскости V, это следует из того, что проекция b лежит на оси х (ордината равна 0) следовательно на рис б, точка b совпадает с bх . Отрезок bхb’ соответствующий отрицательному значению аппликаты откладываем вниз от плоскости Н. Положение самой точки В совпадает с положением ее фронтальной проекции b’.
Точка С располагается на плоскости Н, это следует из того, что проекция с’ лежит (рис. а) на оси х (аппликата точки С равна 0) Поэтому и на рис. б схс’.
Так как для точки С ордината положительна, то соответствующей этой ординате отрезок схс откладывается вправо от плоскости V, положение самой точки совпадает с положением ее горизонтальной проекции с.
Задача № 7.Изобразить наглядно положения точек А,B,C,D и E, заданных своими проекциями на рисунке.
Задача № 8*.Построить проекции точек А и В по их координатам. Построить проекцию точки С, расположенной симметрично точке А относительно фронтальной плоскостей проекций. Изобразить наглядно положения этих точек относительно плоскостей V и Н.
| координаты точка | x | y |
| A | 13,5 | |
| B | 6,5 | -20 |
Решение.Намечаем ось х (рис.а) и на ней точку ах . Так кА точка А положительна, расположена в первой четверти (аппликата и ордината положительны), то проекция а’ находится над осью х на расстоянии 13,5.
Для построения точки В сначала задаемся (на оси х) произвольно точкой bх и откладываем вниз отрезок bх b равный значению ординаты 6,5 и отрезок bх b’, соответствующий отрицательному значению аппликаты (-20). Точка В находится в первой четверти.
Точка С должна быть расположена симметрично точке А относительно плоскости V. Следовательно ордината точки С равна -13,5, а аппликата равно 20. Точка сх совпадает с точкой ах, с’ – с а’, а горизонтальная проекция с находится над осью х на расстоянии 13,5.
Задача № 9.Построить проекции точек А, В, С по их координатам. Построить проекцию точки D ,расположенной симметрично точке С относительно оси х. Изобразить наглядно положения этих точек относительно плоскостей V и Н.
| координаты точка | x | y |
| A | -25 | |
| B | -20 | |
| С | -30 | -20 |
| х |
Задача № 10. Построить недостающие проекции точек А, В, С, D и их наглядное изображение в системе трех плоскостей проекций.
Тема 1.3. Проекции прямой линии. Взаимное положение прямых в пространстве.
| Задача № 11. По заданным фронтальной а2 и профильной а3 проекциям прямой построить горизонтальную проекцию а1 , прямой а |  |
 | Задача № 12. По фронтальному N2 и профильному T3 следам прямой а построить её проекции. Определить через какие октанты она проходит. |
| Задача № 13. По горизонтальному M1 и профильному T3 следам прямой а построить её проекции. Определить через какие октанты она проходит. | 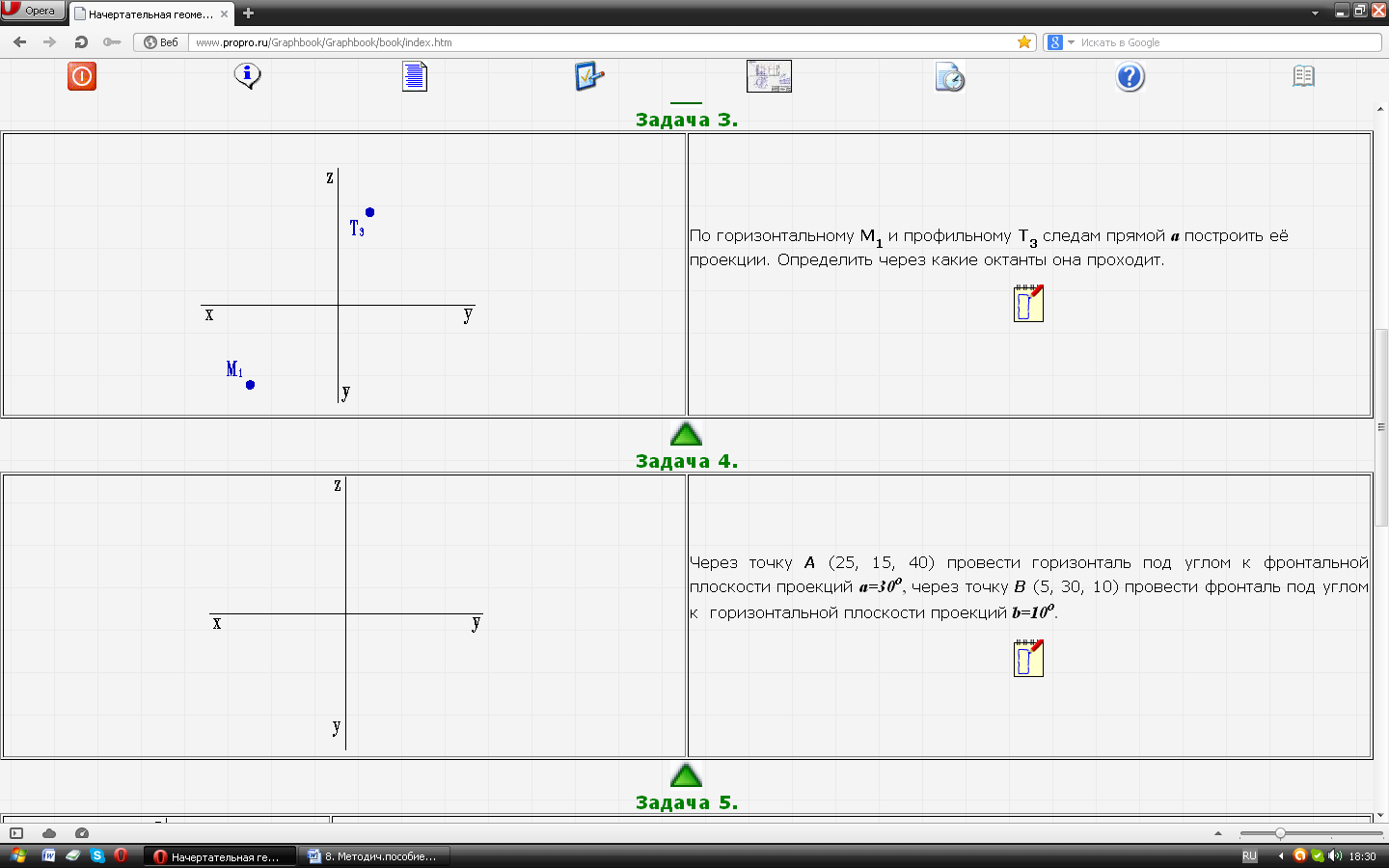 |
| Задача № 14. Через точку А (25, 15, 40) провести горизонталь под углом к фронтальной плоскости проекций a=30 o , через точку В (5, 30, 10) провести фронталь под углом к горизонтальной плоскости проекций b=10 o . | |
 | |
| Задача № 15. Построить три проекции отрезка АВ прямой линии п по заданным координатам ее концов А(30,10,10) , В(10,25,40). Построить проекции точки С, делящей отрезок в отношении АС:СВ=1:2. | |
 | |
| Задача № 16. Построить следы прямой линии заданной отрезком | 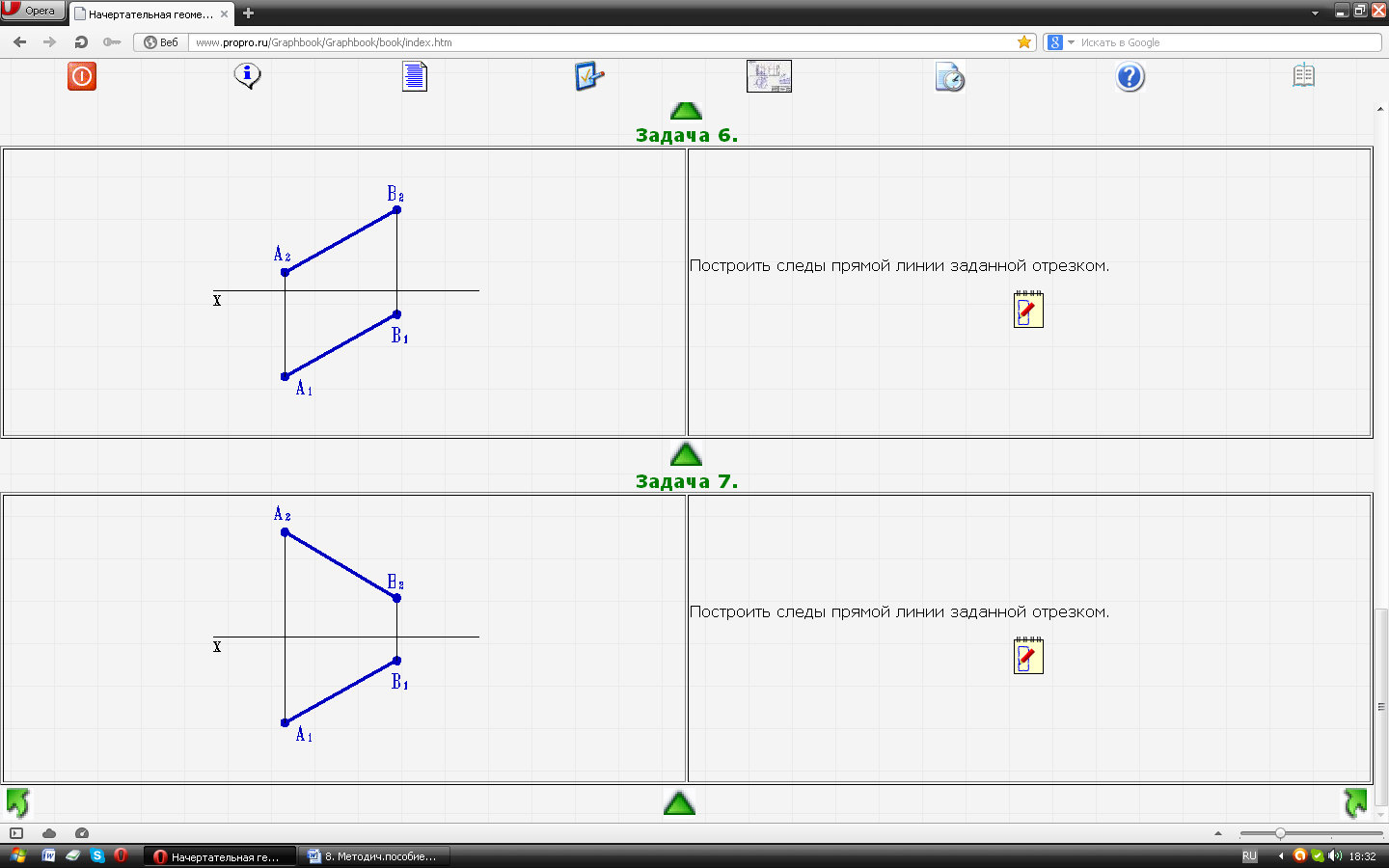 |
 | Задача № 17. Построить следы прямой линии заданной отрезком |
| Взаимное расположение точки и прямой | |
| Задача № 18.Определить какая из предложенных на проекциях точек принадлежит прямой m. |  |
 | Задача № 19.Построить проекции точки А равноотстоящей от плоскостей П1 и П2 и принадлежащей прямой а заданной на эпюре. |
| Задача № 20.Построить недостающие проекции точек А и В, если известно, что точка А лежит на прямой п, а В на 10 мм выше точки А. |  |
 | Взаимное расположение прямых Задача № 21.Через точку Е провести прямую, пересекающую прямые АВ и СD. |
Тема 1.4. Плоскость.
| Задача № 22.По координатам трех точек А(45,30,10), B(30,10,45) и С(5,25,5) построить проекции плоскости и её следы. | 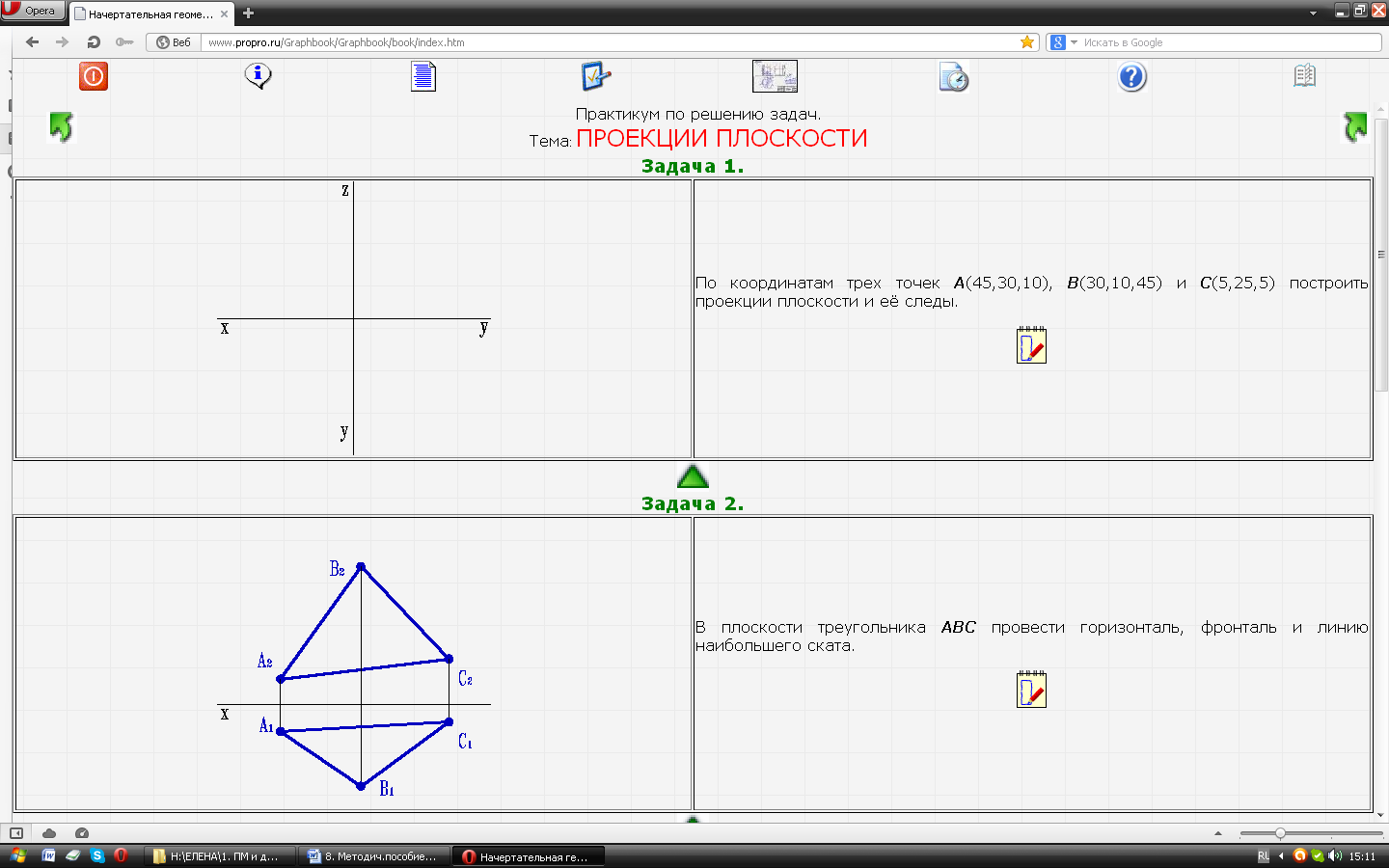 |
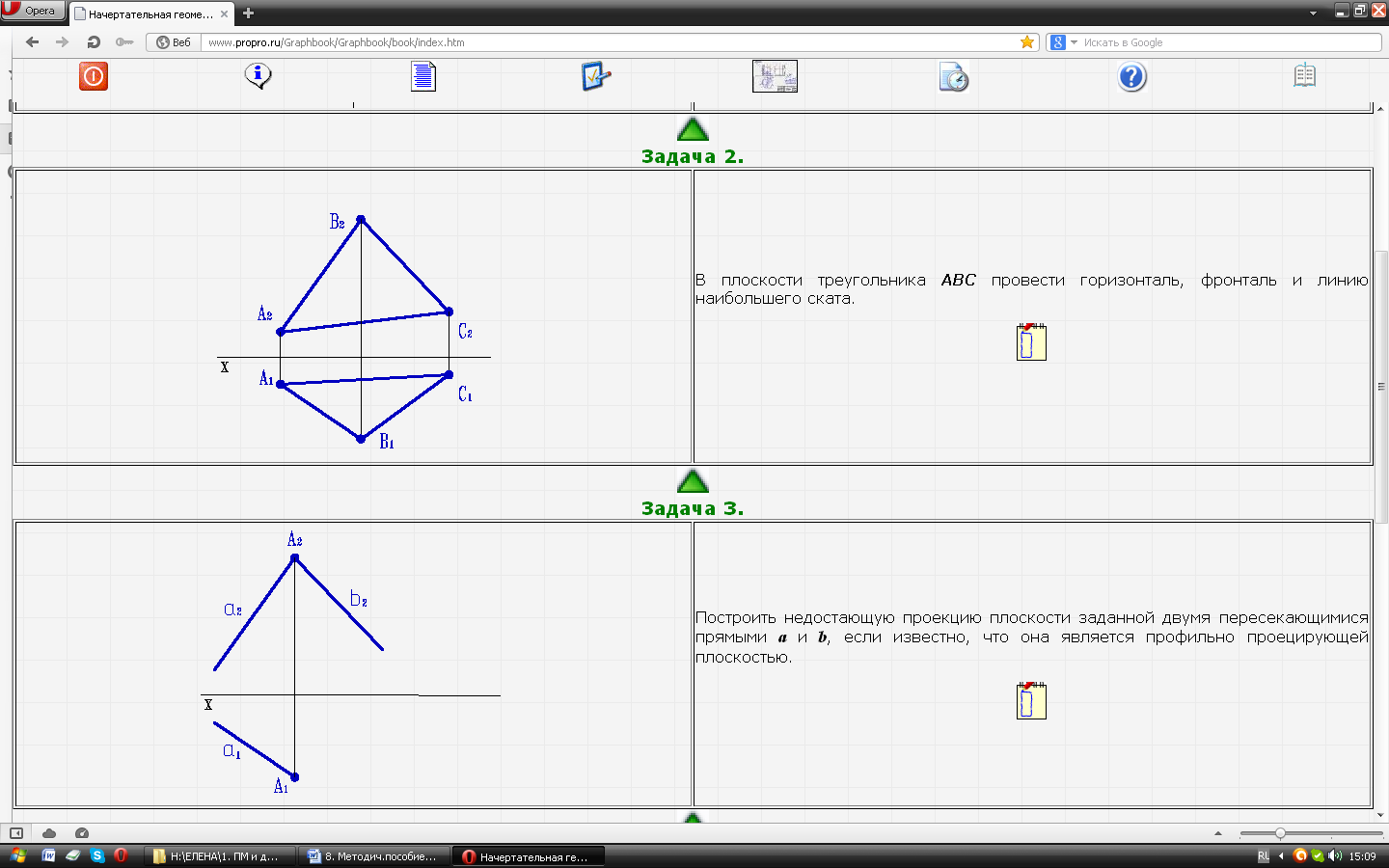 | Задача № 23. В плоскости треугольника АВС провести горизонталь, фронталь и линию наибольшего ската. |
| Задача № 24.Построить недостающую проекцию плоскости заданной двумя пересекающимися прямыми a и b, если известно, что она является профильно проецирующей плоскостью. |  |
Тема 1.5. Задание точки и прямой в плоскости.
Прямая и точка в плоскости. Главные линии плоскости. Пересечение прямой и плоскости. Определение видимости на чертеже.
| Задача № 25 Построить недостающую проекцию точки D принадлежащей плоскости АВС. | 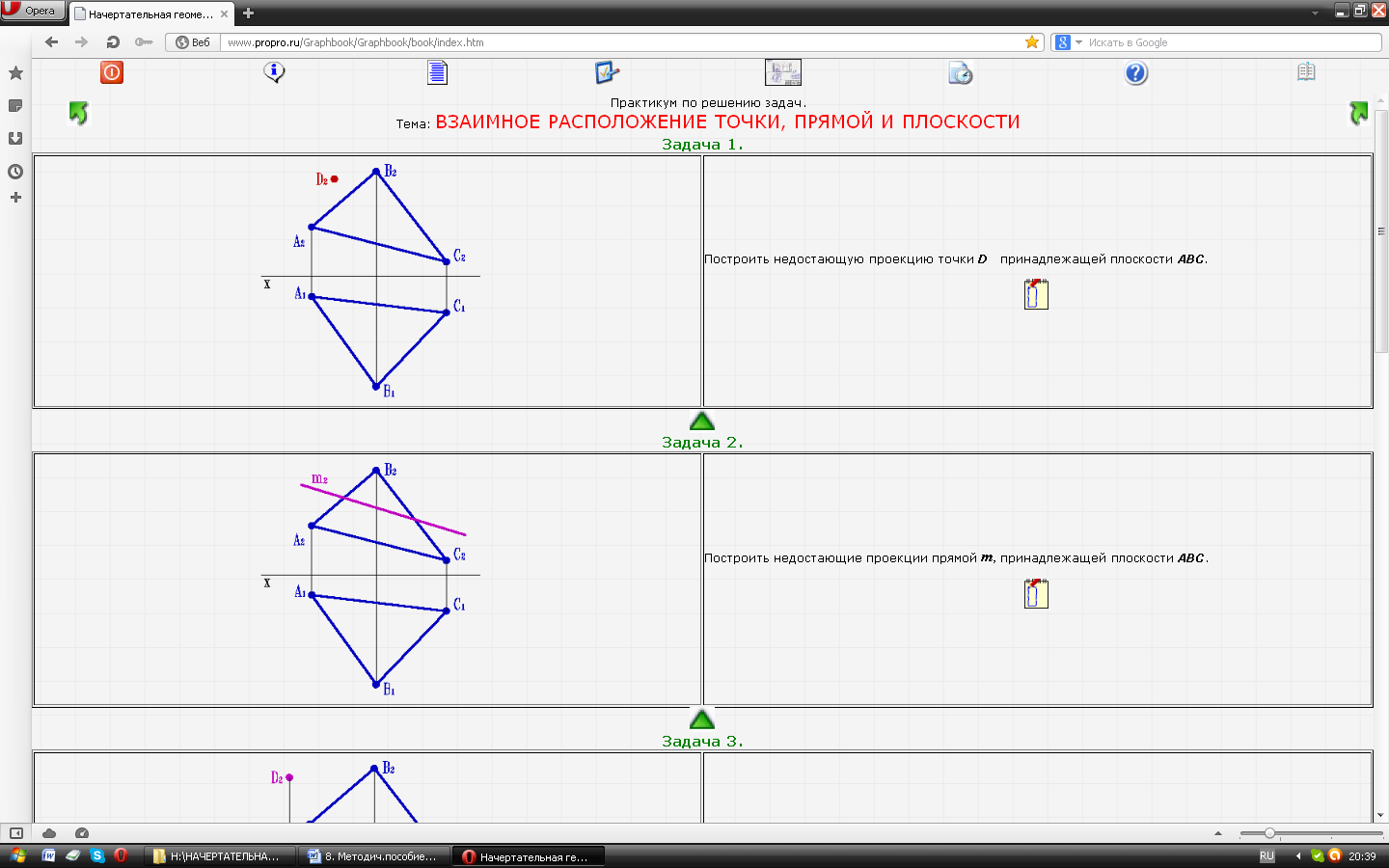 |
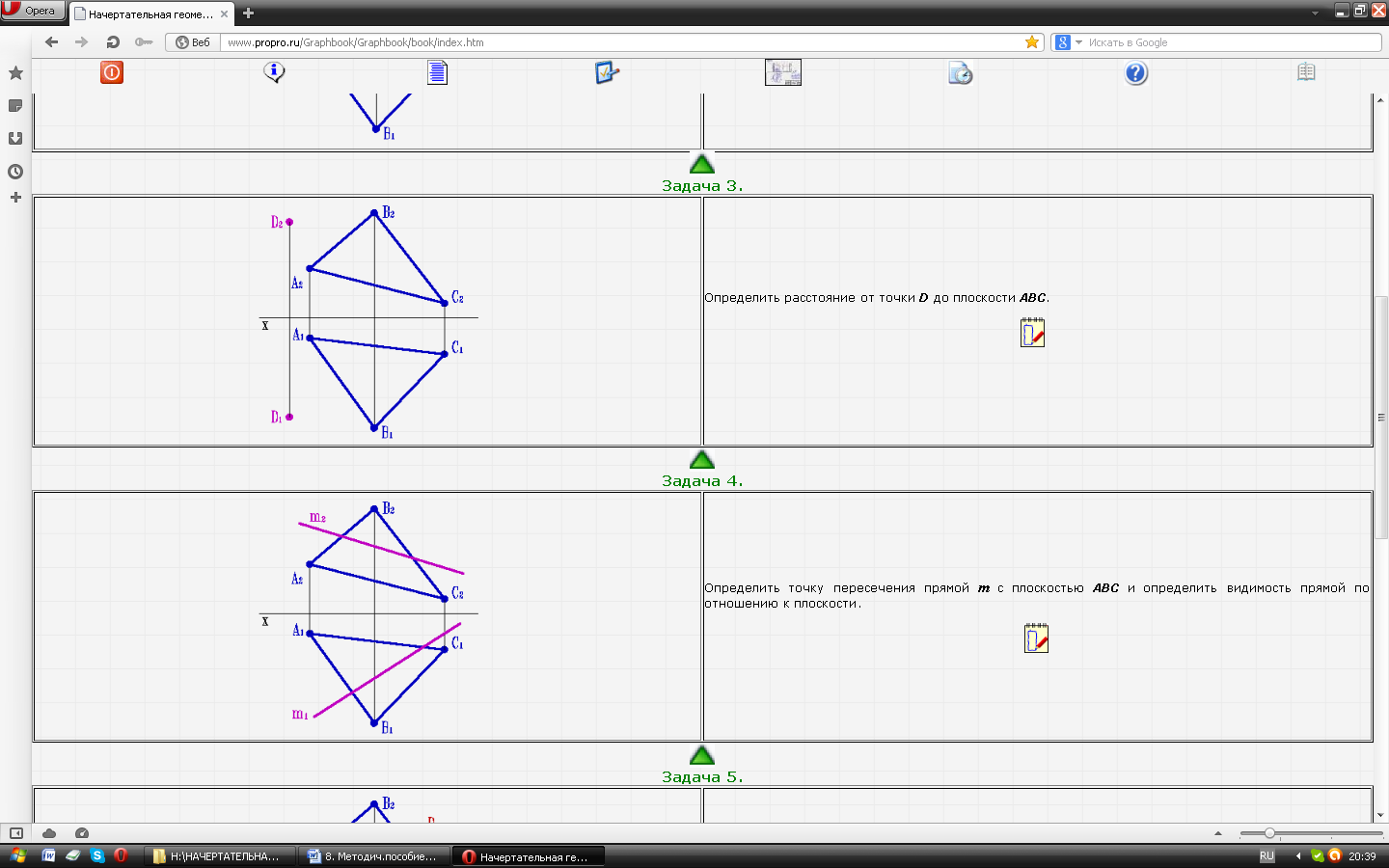 | Задача № 26. Определить расстояние от точки D до плоскости АВС |
 | Задача № 27. Построить недостающие проекции прямой m, принадлежащей плоскости АВС.. |
| Задача № 28 Определить точку пересечения прямой m с плоскостью АВС и определить видимость прямой по отношению к плоскости. |  |
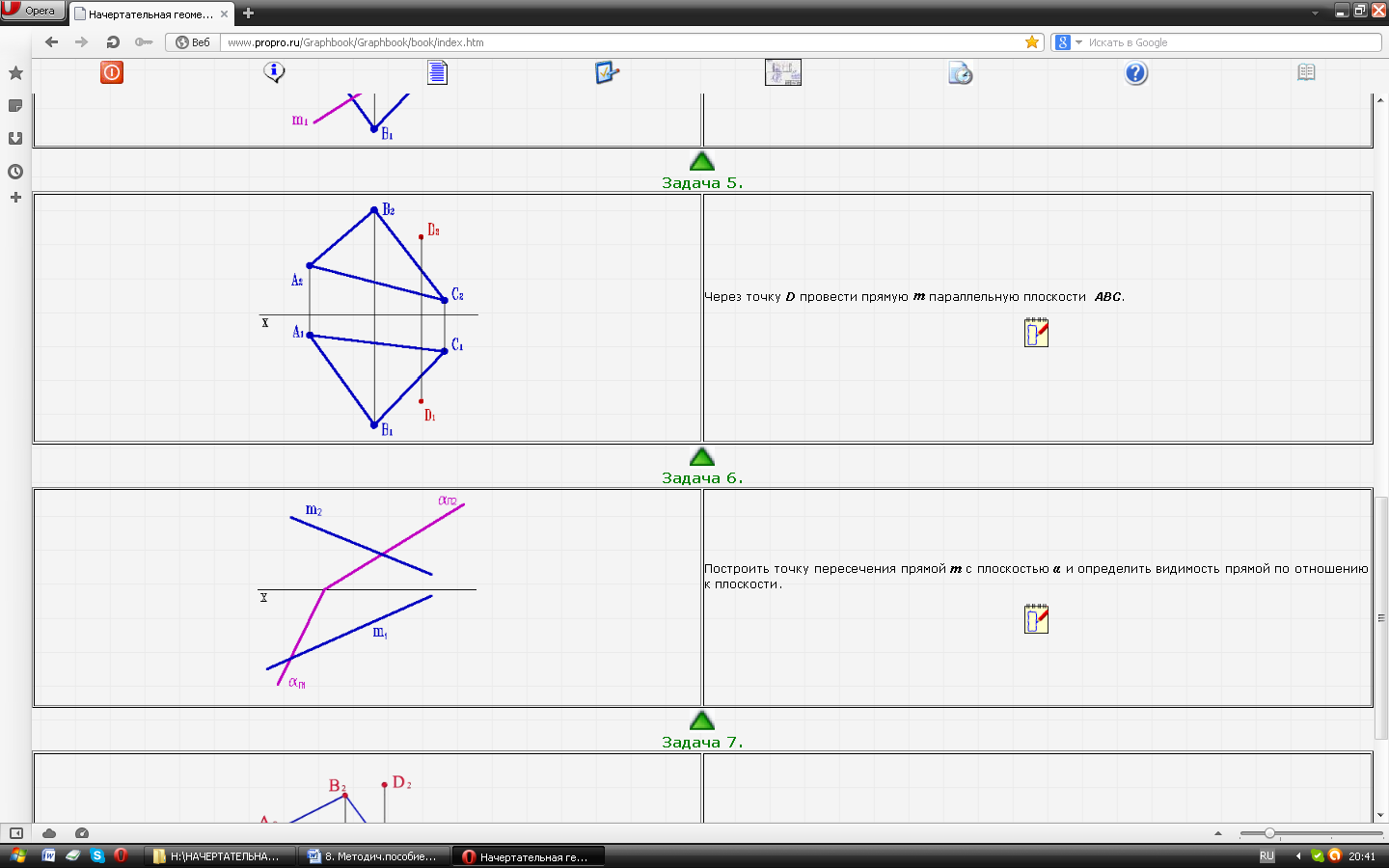 | Задача № 29. Через точку D провести прямую параллельную плоскости АВС. |
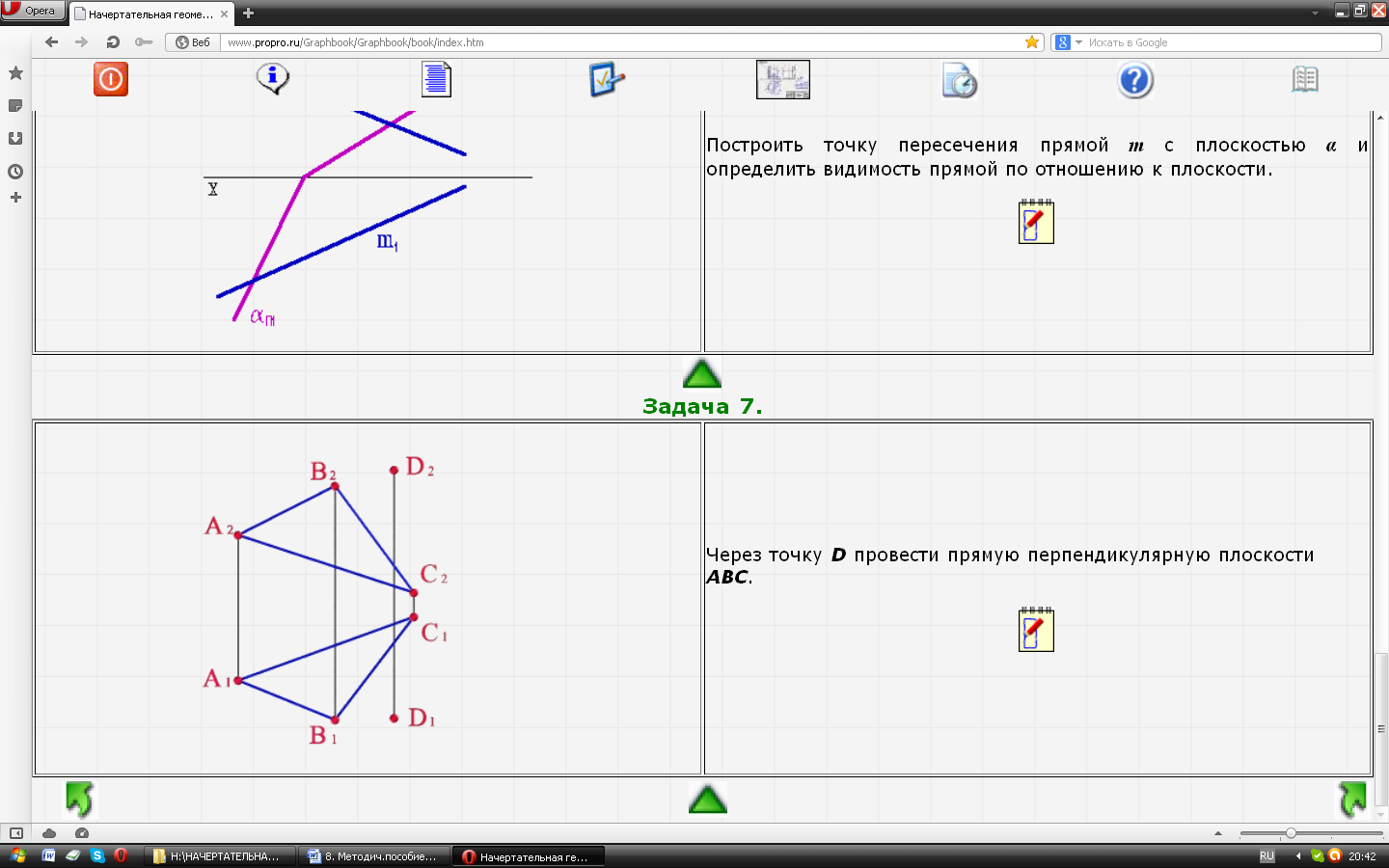 | Задача № 30. Через точку D провести прямую перпендикулярную плоскости АВС. |
| Тема 1.6.Взаимное положение плоскостей. | |
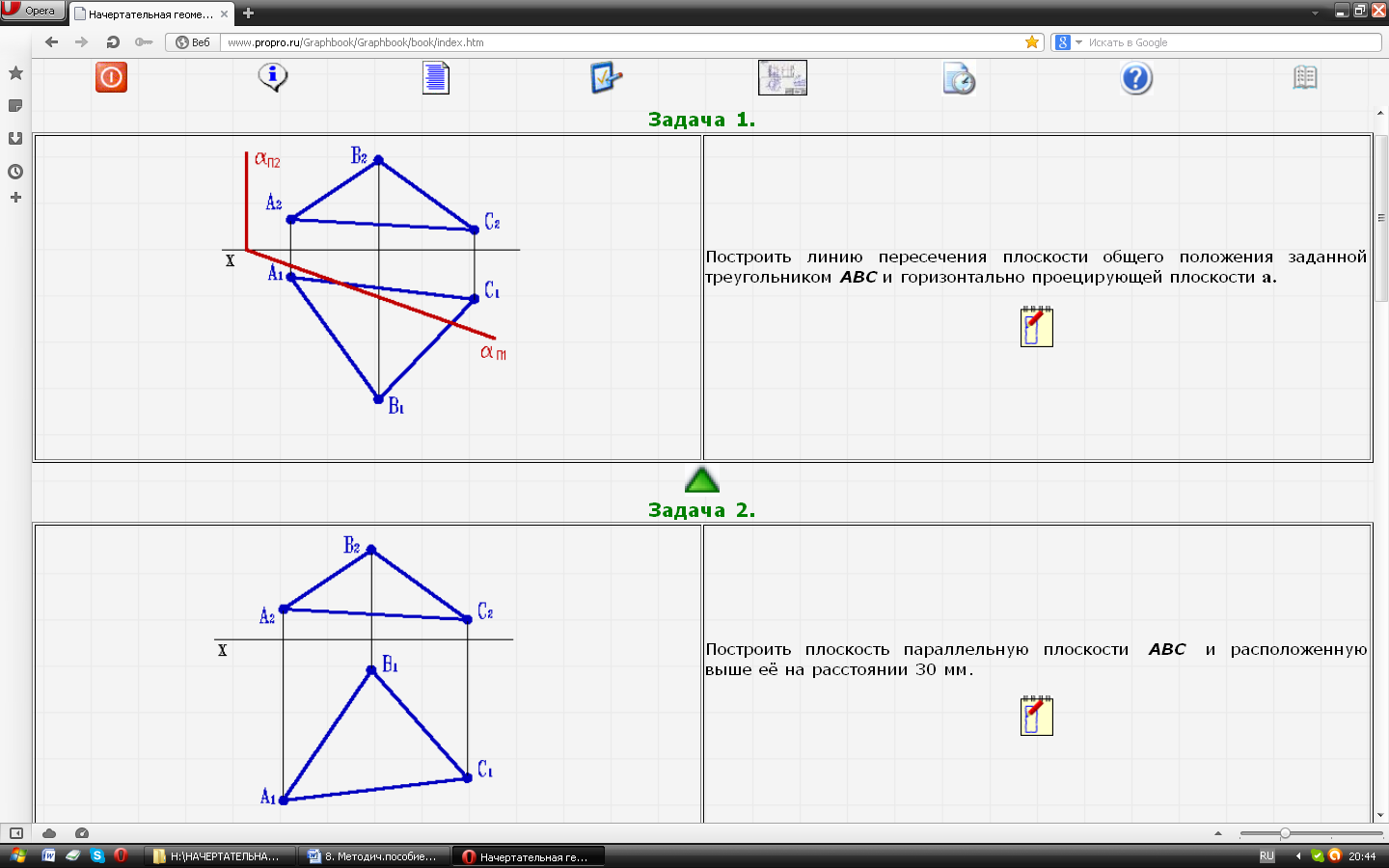 | Задача № 31. Построить плоскость параллельную плоскости АВС и расположенную выше её на расстоянии 30 мм. |
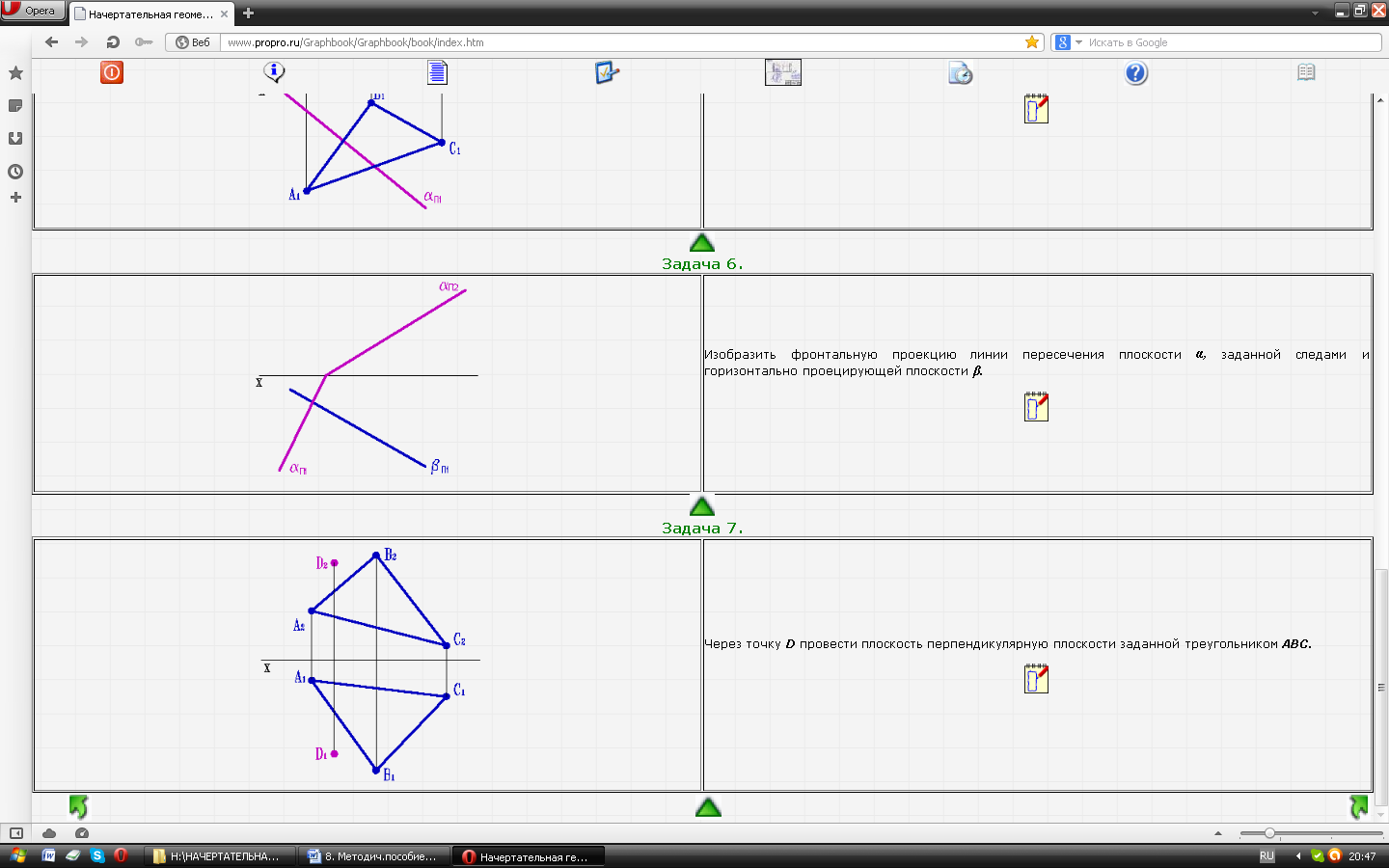 | Задача № 32. Через точку D провести плоскость перпендикулярную плоскости заданной треугольником АВС. |
| Задача № 33. Построить линию пересечения плоскости АВС и плоскости заданной двумя параллельными прямыми п и т. Определить видимость. | 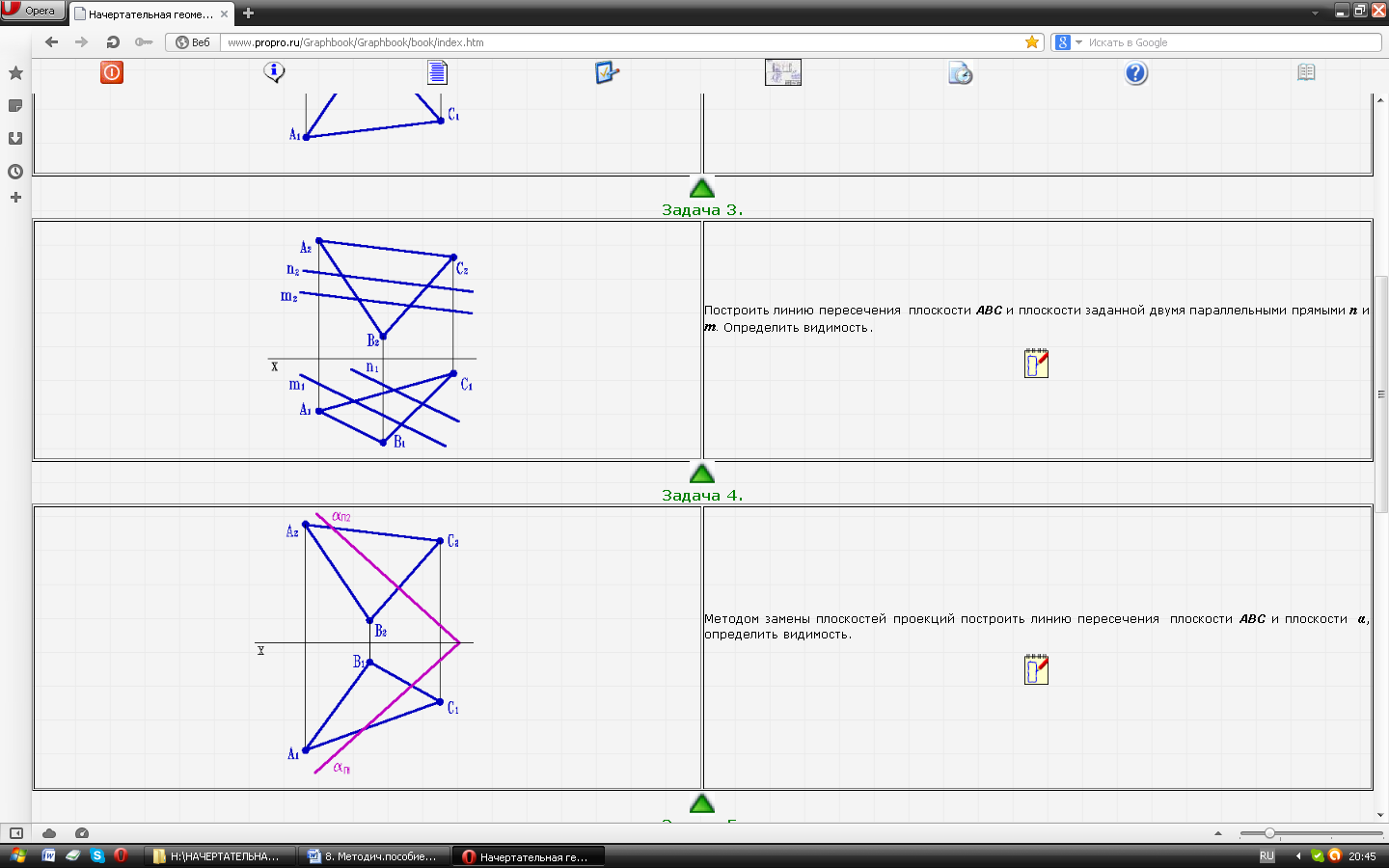 |
Тема 1.7.Способы преобразования проекционного чертежа.
Источник
Метод вращения вокруг оси
Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.
Способ вращения вокруг проецирующей прямой
Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.
- Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
- При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
- При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.
Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.
При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’1 так, чтобы выполнялось условие C’1D’1 || X. Для нахождения точки C»1 из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’1.
На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.
Сначала вращением вокруг оси i1 CD перемещают в положение C1D1, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i2 отрезок переводится в искомое положение C2D2, где он перпендикулярен горизонтальной плоскости проекции.
Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i1 проходит через точку D, а проекция i»2 фронтально проецирующей прямой i2 лежит на продолжении отрезка C»1D»1.
Способ вращения вокруг линии уровня
Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.
Основные правила построения
- Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
- При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
- При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.
Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.
- Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
- Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
- Определяем натуральную величину радиуса вращения R = O’A’0. Для этого строим прямоугольный треугольник O’A’A’0, катет которого A’A’0 равен расстоянию от A» до h».
- Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’1. Соединяем A’1 с точками 1′ и 2′. Искомый угол ϕ построен.
Источник