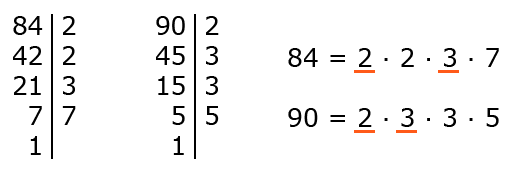НОД, НОД
НОД — это наибольший общий делитель.
НОК — это наименьшее общее кратное.
Определения:
- Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.
- Наименьшее общее кратное (НОК) двух целых чиселm и n есть наименьшее натуральное число , которое делится на m и n без остатка
Способы нахождения НОД двух чисел:
1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Выписываем все делители числа а;
- Выписываем все делители числа b;
- Выбираем среди них общие делители;
- Среди общих делителей выбираем самое большое число – это и есть НОД(a, b).
2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД) натуральных чисел.
- Найти делители меньшего из данных чисел.
- Найти, начиная с большего, тот из выписанных делителей, который является также делителем другого числа.
- Записать найденное число – НОД.
3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.
- Находим разложение чисел на простые множители.
- Подчеркиваем общие числа.
- Находим произведение подчеркнутых чисел у одного числа.
- Записываем ответ.
4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел вычитанием.
- Из большего числа вычитается меньшее.
- Если получается 0, то числа равны друг другу и являются наибольшим общим делителем.
- Если результат вычитания не равен 0, то большее число заменяется на результат вычитания.
- Переход к пункту 1.
Способы нахождения НОК двух чисел:
1 способ: Метод перебора
1. Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
2 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители
- Разложить данные числа на простые множители.
- Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
- Подчеркнуть в разложении меньшего числа множители, которые не вошли в разложение бóльшего числа и добавить эти множители в разложение большего числа.
- Полученное произведение записать в ответ.
Свойства наибольшего общего делителя:
- НОД(a, b) = НОД(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОД(a, 0) = |a|
- НОД(a, к • a) = |a|, при любом к ∈ Z
- НОД(a, НОД(b, с)) = НОД(НОД(a, b), c)
Свойства наименьшего общего кратного:
- НОК(a, b) = НОК(b, a)
- НОД(a, b) = НОД(-a, b)
- НОД(a, b) = НОД(|a|,|b|)
- НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)
Источник
Наибольший общий делитель (НОД), свойства и формулы
О чем эта статья:
5 класс, 6 класс
Понятие наибольшего общего делителя
Начнем с самого начала и вспомним, что такое общий делитель. У целого числа может быть несколько делителей. А сейчас нам особенно интересно, как обращаться с делителями сразу нескольких целых чисел.
Делитель натурального числа — это такое натуральное число, которое делит данное число без остатка. Если у натурального числа больше двух делителей, его называют составным.
Общий делитель нескольких целых чисел — это такое число, которое может быть делителем каждого числа из указанного множества. Например, у чисел 12 и 8 общим делителем будет четверка. Чтобы это проверить, напишем верные равенства: 8 = 4 * 2 и 12 = 3 * 4. Но у этой пары чисел есть и другие общие делители: 1, -1 и -4.
Любое число можно разделить на 1, -1 и на само себя. Значит у любого набора целых чисел будет как минимум три общих делителя. Если общий делитель больше 0 — противоположное ему значение со знаком минус также является общим делителем.
Если b — делитель целого числа a, которое не равно нулю, то модуль числа b не может быть больше модуля числа a. Значит любое число, не равное 0, имеет конечное число делителей.
Наибольшим общим делителем двух чисел a и b называется наибольшее число, на которое a и b делятся без остатка. Для записи может использоваться аббревиатура НОД. Для двух чисел можно записать вот так: НОД (a, b).
Например, для 4 и -16 НОД будет 4. Как мы к этому пришли:
Проверить результаты вычислений можно с помощью онлайн-калькулятора НОД и НОК.
- Зафиксируем все делители четырех: ±4, ±2, ±1.
- А теперь все делители шестнадцати: ±16, ±8, ±4, ±3 и ±1.
- Выбираем общие: это -4, -2, -1, 1, 2 и 4. Самое большое общее число: 4. Вот и ответ.
Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.
Найдем наибольший общий делитель нескольких целых чисел: 10, 6, 44, -18. Он будет равен трем. Ответ можно записать так: НОД (12, 6, 42, -18) = 3. А чтобы проверить правильность ответа, нужно записать все делители и выбрать из них самые большие.
Взаимно простые числа — это натуральные числа, у которых только один общий делитель — единица. Их НОД равен 1.
Помимо НОД есть еще и НОК, что расшифровывается, как наименьшее общее кратное и означает наименьшее число, которое делится на каждое из исходных чисел без остатка.
Еще один пример. Рассчитаем НОД для 28 и 64.
- Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Свойства наибольшего общего делителя
У наибольшего общего делителя есть ряд определенных свойств. Опишем их в виде теорем и сразу приведем доказательства.
Важно! Все свойства НОД будем формулировать для положительных целых чисел, при этом будем рассматривать делители только больше нуля.
Свойство 1. Наибольший общий делитель чисел а и b равен наибольшему общему делителю чисел b и а, то есть НОД (a, b) = НОД (b, a). Перемена мест чисел не влияет на конечный результат.
Доказывать свойство не имеет смысла, так как оно напрямую исходит из самого определения НОД.
Свойство 2. Если а делится на b, то множество общих делителей чисел а и b совпадает со множеством делителей числа b, поэтому НОД (a, b) = b.
Доказательство
Любой общий делитель чисел а и b является делителем каждого из этих чисел, в том числе и числа b. Так как а кратно b, то любой делитель числа b является делителем и числа а, благодаря свойствам делимости. Из этого следует, что любой делитель числа b является общим делителем чисел а и b.
Значит, если а делится на b, то совокупность делителей чисел а и b совпадает с совокупностью делителей одного числа b. А так как наибольшим делителем числа b является само число b, то наибольший общий делитель чисела и b также равен b, то есть НОД (а, b) = b.
В частности, если a = b, то НОД (a, b) = НОД (a, a) = НОД (b, b) = a = b.
- Например, НОД (25, 25) = 25.
Доказанное свойство наибольшего делителя можно использовать, чтобы найти НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число.
- Например, НОД (4, 40) = 4, так как 40 кратно 4.
Свойство 3. Если a = bq + c, где а, b, с и q — целые числа, то множество общих делителей чисел а и b совпадает со множеством общих делителей чисел b и с. Равенство НОД (a, b) = НОД (b, c) справедливо.
Доказательство
Существует равенство a = bq + c, значит всякий общий делитель чисел а и b делит также и с, исходя из свойств делимости. По этой же причине, всякий общий делитель чисел b и с делит а. Поэтому совокупность общих делителей чисел а и b совпадает с совокупностью общих делителей чисел b и c.
Поэтому должны совпадать и наибольшие из этих общих делителей, и равенство НОД (a, b) = НОД (b, c) можно считать справедливым.
Свойство 4. Если m — любое натуральное число, то НОД (mа, mb) = m * НОД(а, b).
Доказательство
Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (mа, mb)= mr, где r — это НОД (а, b). На этом свойстве наибольшего общего делителя основан поиск НОД с помощью разложения на простые множители.
Свойство 5. Пусть р — любой общий делитель чисел а и b, тогда НОД (а : p, b : p) = НОД (а, b) : p. А именно, если p = НОД (a, b) имеем НОД (a : НОД (a, b), b: НОД (a, b)) = 1, то есть, числа a : НОД (a, b) и b : НОД (a, b) — взаимно простые.
Так как a = p(a : p) и b = p(b : p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД (a, b) = НОД (p(a : p), p(b : p)) = p * НОД (a : p, b : p), откуда и следует доказываемое равенство.
Способы нахождения наибольшего общего делителя
Найти наибольший общий делитель можно двумя способами. Рассмотрим оба, чтобы при решении задач выбирать самую оптимальную последовательность действий.
1. Разложение на множители
Чтобы найти НОД нескольких чисел, достаточно разложить их на простые множители и перемножить между собой общие множители для всех чисел.
Пример 1. Найти НОД (84, 90).
- Разложим числа 84 и 90 на простые множители:
Подчеркнем все общие множители и перемножим их между собой:
Ответ: НОД (84, 90) = 6.
Пример 2. Найти НОД (15, 28).
- Разложим 15 и 28 на простые множители:
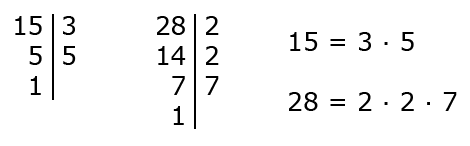
Ответ: НОД (15, 28) = 1.
Пример 3. Найти НОД для 24 и 18.
- Разложим оба числа на простые множители:
Найдем общие множители чисел 24 и 18: 2 и 3. Для удобства общие множители можно подчеркнуть.
Перемножим общие множители:
НОД (24, 18) =2 * 3 = 6
Ответ: НОД (24, 18) = 6
2. Алгоритм Евклида
Способ Евклида помогает найти НОД через последовательное деление. Сначала посмотрим, как работает этот способ с двумя числами, а затем применим его к трем и более.
Алгоритм Евклида заключается в следующем: если большее из двух чисел делится на меньшее — наименьшее число и будет их наибольшим общим делителем. Использовать метод Евклида можно легко по формуле нахождения наибольшего общего делителя.
Формула НОД: НОД (a, b) = НОД (b, с), где с — остаток от деления a на b.
Пример 1. Найти НОД для 24 и 8.
Так как 24 делится на 8 и 8 тоже делится на 8, значит, 8 — общий делитель этих чисел. Этот делитель является наибольшим, потому что 8 не может делиться ни на какое число, большее его самого. Поэтому: НОД (24, 8) = 8.
В остальных случаях для нахождения наибольшего общего делителя двух чисел нужно соблюдать такой порядок действий:
- Большее число поделить на меньшее.
- Меньшее число поделить на остаток, который получается после деления.
- Первый остаток поделить на второй остаток.
- Второй остаток поделить на третий и т. д.
- Деление продолжается до тех пор, пока в остатке не получится нуль. Последний делитель и есть наибольший общий делитель.
Пример 2. Найти наибольший общий делитель чисел 140 и 96:
- 140 : 96 = 1 (остаток 44)
- 96 : 44 = 2 (остаток 8)
- 44 : 8 = 5 (остаток 4)
- 8 : 4 = 2
Последний делитель равен 4 — это значит: НОД (140, 96) = 4.
Ответ: НОД (140, 96) = 4
Пошаговое деление можно записать столбиком:
Чтобы найти наибольший общий делитель трех и более чисел, делаем в такой последовательности:
- Найти наибольший общий делитель любых двух чисел из данных.
- Найти НОД найденного делителя и третьего числа.
- Найти НОД последнего найденного делителя и четвёртого числа и т. д.
Знакомство с темой наибольшего общего делителя начинается в 5 классе с теории и закрепляется в 6 классе на практике. В этой статье мы узнали все основные определения, свойства и их доказательства, а также как найти НОД.
Источник