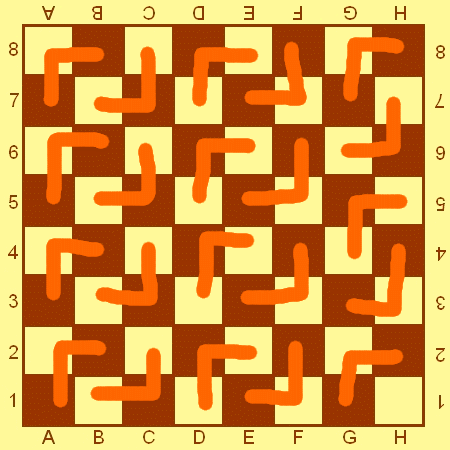ОЛИМПИАДА ПО МАТЕМАТИКЕ. МОЖЕТЕ СКИДОВАТЬ ОТВЕТЫ ПО ОДНОЙ ЗАДАЧЕ. Заранее спасибо.
Задача 1. Сумма двух
Чему равна сумма двух чисел, если она в 7 раз больше одного из них и на 8 больше другого?
Задача 2. Много цифр
Пару соседних цифр в многозначном числе назовем хорошей, если при их перестановке число увеличивается. Какое наибольшее количество цифр может быть в многозначном числе, если известно, что все пары соседних
цифр в нём, кроме 3, хорошие?
Задача 3. Строчки и столбики
В квадрате 160 × 160 закрашено несколько клеток. В каждой строчке есть либо 1, либо 7 закрашенных клеток, а в каждом столбце есть либо 3, либо 4 закрашенных клетки. Какое наименьшее число клеток может быть закрашено?
Задача 4. Большой куб
Мистер Фокс сложил большой куб из одинаковых маленьких кубиков.
Затем он покрасил некоторые грани получившегося большого куба, а затем разобрал его обратно на маленькие кубики.
Число кубиков, у которых нет ни одной покрашенной грани, оказалось равно 45.
У скольких кубиков есть хоть одна покрашенная грань?
Задача 5. Десять квадратов
Прямоугольник разделён на 10 квадратов.
Периметр закрашенного квадрата равен 72.
Найдите площадь исходного прямоугольника.
РИСУНОК ЕСТЬ ВНИЗУ.
Задача 6. Отметки
В дневнике Поли в текущей четверти стоит 16 отметок по математике; в дневнике Тани — такое же число отметок по тому же предмету. Поля получила пятёрок столько же, сколько Таня четвёрок, четвёрок столько же, сколько Таня троек, троек столько же, сколько Таня двоек, и двоек столько же, сколько Таня – пятёрок. При этом средний балл в этой четверти у девочек одинаковый. Сколько двоек получила Поля?
Задача 7. Вычёркиваем цифры
Сколько существует 2015-значных чисел таких, что при вычёркивании его любой одной цифры получается 2014-значное число, и это 2014-значное число является делителем исходного числа (Напомним, что многозначное число не может начинаться с нуля и что на ноль ничего не делится, кроме, быть может, нуля)?
Задача 8. Тупые углы
На плоскости из одной точки отложено 24 лучей. Какое наибольшее количество тупых углов могут образовывать пары этих лучей?
Задача 10. Лестница
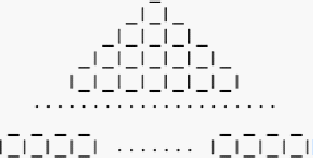
Дана клетчатая фигура в виде лестницы, содержащей n ступенек (на рисунке приведён пример для n=11).
Сколько значений n, удовлетворяющих неравенству 300 Лучший ответ
1) Раз сумма в 7 раз больше числа, то сотношение чисел 1:6. Решение в одну строку.
2) Хорошая пара = вторая цифра меньше первой. Найдите наибольшее количество хороших пар в числе. Решение в одну строку.
3) Столбцы. К квадрате не менее 160*3 закрашенных клеток. Строки. Будем увеличивать это число до тех пор, пока мы не сможем обеспечить нужное количество в строках. А это означает «можно отнять 160 по 1 клетке, остаток (по 6 клеток) должен делиться на 6». Ну и пример обязателен.
4) Оценить 45 сверху и снизу в зависимости от стороны куба n. Т. е. число незакрашенных кубиков должно быть менее . и не менее . Решение в две строки.
5) Найти сторону закрашенного, потом найти сторону маленького, потом — среднего. Устная задача.
6) Обозначить количество каждой оценки буквами (всего 4 буквы в задаче) и всё записать. Решение в две строки.
Источник
Найти количество способов закрасить некоторые клетки лесенки
Оценка. 10 лошадей — это 40 копыт. Если кузнецы выполняют одинаковый объём работы (по-другому работать невыгодно, так как производительность у всех одинаковая), то каждый должен подковать 40 : 8 = 5 копыт, потратив на это 5·5 = 25 минут (в случае, если им всем удастся работать одновременно так, чтобы никакая лошадь не стояла на двух ногах). Так же делается оценка в пункте б.
Пример. Разобьём кузнецов на группы по 4, а лошадей — на группы по 5. В пункте а таких групп будет по две, а в пункте б — по 12. Каждая группа кузнецов будет работать со своей группой лошадей по следующему графику:
| Время | I кузнец | II кузнец | III кузнец | IV кузнец |
| 1-5 минуты | 1 | 2 | 3 | 4 |
| 6-10 минуты | 2 | 3 | 4 | 5 |
| 11-15 минуты | 3 | 4 | 5 | 1 |
| 16-20 минуты | 4 | 5 | 1 | 2 |
| 21-25 минуты | 5 | 1 | 2 | 3 |
В этой таблице указан номер лошади, которую в соотвествующий момент времени подковывает кузнец. В каждой строке все лошади разные, значит, никакой лошади не нужно стоять на двух ногах. Каждый номер от 1 до 5 встречается в таблице 4 раза, значит, каждой лошади подковали все 4 ноги.
а) Чтобы число делилось на 10, оно должно оканчиваться на 0. Если число будет двузначным с нулём на конце, то его сумма цифр будет не больше 9. Значит, число должно быть по крайней мере трёхзначным. Наименьшим из трёхзначных чисел с указанными свойствами будет то, у которого в разряде сотен стоит единица. Чтобы сумма цифр этого числа была равна 10, в разряде десятков у него должна стоять девятка.
б) Чтобы число делилось на 100, оно должно оканчиваться двумя нулями. Если число будет не более чем 13-значным с двумя нулями на конце, то (поскольку каждая цифра не больше 9) сумма его цифр будет не больше 99. Значит, число должно быть по крайней мере 14-значным. Из 14-значных чисел с указанными свойствами наименьшим числом будет то, у которого в старшем разряде единица. Тогда остальные его цифры (кроме двух нулей на конце) должны быть девятками, и это будет число 19999999999900.
в) Чтобы число делилось на 5, оно должно оканчиваться нулём или пятёркой. Если число не более чем трёхзначное и оканчивается нулём или пятёркой, то сумма его цифр не больше 5+9+9 = 23. Значит, число должно быть по крайней мере четырёхзначным. Среди четырёхзначных чисел с указанными свойствами наименьшим будет то, у которого в разряде тысяч стоит наименьшая цифра. Если там стоит единица, то сумма цифр числа не превосходит 1+9+9+5 = 24. Значит, там должна стоять хотя бы двойка. В последнем случае сумма цифр 25 достижима, только если это число 2995. Остальные числа с указанными свойствами будут больше найденного.
Оценка. Разобъём наш квадрат на 16 квадратиков 2×2. В пункте а в каждом из них должна быть хотя бы одна закрашенная клетка (иначе будет квадратик без закрашенных клеток), так что клеток не меньше 16. В пункте б в каждом из этих квадратиков должно быть хотя бы две закрашенные клетки, иначе в этом квадратике поместится незакрашенный уголок. Поэтому в пункте б нужно закрасить
Пример. В пункте а закрасим на доске клетки A1, A3, A5, A7, C1, C3, C5, C7, E1, E3, E5, E7, G1, G3, G5, G7 (обозначения клеток — как на шахматной доске). Легко видеть, что закрашено 16 клеток, и при этом в любом квадратике 2×2 есть ровно одна закрашенная клетка. В пункте б можно использовать, например, обычную шахматную раскраску: при этом будет закрашено 32 клетки, а в каждом трёхклеточном уголке будет либо одна белая клетка и две чёрных, либо одна чёрная и две белых.
Оценка: двух аудиторий может не хватить. В самом деле, если среди шестиклассников есть трое попарно знакомых, то их нельзя посадить ни в одну, ни в две аудитории.
Пример: трёх аудиторий всегда хватит. Объясним, как можно рассадить школьников по трем аудиториям. Всех школьников можно разделить на несколько групп так, чтобы школьники из разных групп между собой знакомы не были (может быть, такая группа будет только одна). Тогда эти группы можно рассаживать по аудиториям независимо друг от друга.
Внутри каждой группы возможна только одна из двух ситуаций. Либо первый человек знаком со вторым, второй с третьим, третий с четвёртым, . предпоследний с последним, последний с первым. Либо всё то же самое, только первый и последний не знакомы. Другие ситуации невозможны, потому что у каждого школьника не больше двух знакомых. (Некоторые группы могут состоять и всего из одного человека, который ни с кем не знаком.) Во втором случае всю группу можно рассадить в две аудитории (школьников с нечётными номерами — в первую аудиторию, школьников с чётными — во вторую). В первом случае делаем то же самое, а если школьников в группе нечётное число, то последнего придётся посадить в третью аудиторию (он знаком с первым, сидящим в первой аудитории, и с предпоследним, номер которого чётный и который поэтому сидит во второй аудитории).
Пример. Первый едет треть пути на самокате, бросает его, бежит дальше пешком. Второй бежит треть пути, хватает валяющийся самокат, берёт его, едет треть пути, бросает, бежит дальше пешком. Третий бежит две трети пути, хватает самокат и финиширует одновременно со сокомандниками. В итоге каждый треть пути (1 км) едет и две трети пути (2 км) бежит. Значит, каждый спортсмен тратит 1000:250 + 2000:125 = 20 минут на преодоление дистанции.
Оценка. Очевидно, что возвращаться назад, чтобы передать транспортное средство товарищу, невыгодно. Поэтому на самокате нужно двигаться только вперёд. Если кто-то проедет на самокате менее трети дистанции, то он потратит на весь забег более 20 минут. Значит, всем нужно проехать ровно треть.
Оценка. Разные прямоугольники — разные по форме или по площади. Прямоугольников площадью в одну клеточку может быть не более одного, площадью в две и в три клеточки — тоже. А вот в 4 клеточки уже может быть два варианта: прямоугольник 1×4 и квадрат 2×2. Таким образом, прямоугольник площадью 1+2+3+4+4=14 клеток можно разрезать не более чем на 5 различных прямоугольников.
Минимальные площади прямоугольников: 1, 2, 3, 4, 4, 5, 6, 6, 7, 8, 8, 9, 9, .
Аналогичные рассуждения приводят к ответам: а) Площадь равна 30, можно сделать не более 7 прямоугольников.
б) Площадь равна 72; не более 13 прямоугольников.
в) Площадь 72; но прямоугольник 3—3 не помещается внутри прямоугольника 2×36, поэтому его использовать нельзя; в итоге получаем не более 12 прямоугольников.
Примеры. На рисунках ниже показано, как разрезать прямоугольник 5×6 на 7 прямоугольников, 12×6 на 13 прямоугольников и прямоугольник 2×36 на 12 прямоугольников.
Источник
Найти количество способов закрасить некоторые клетки лесенки
а) Обозначим искомую сумму S:
S = 1 + 2 + 3 + . + 50
Теперь запишем ту же сумму в обратном порядке:
S = 50 + 49 + 48 + . + 1
Напишем эти формулы одну под другой и «сложим в столбик», складывая слагаемые, написанные друг под другом:
S = 1 + 2 + 3 + . + 50
S = 50 + 49 + 48 + . + 1
2S = 51 + 51 + 51 + . + 51
В последней сумме 50 слагаемых (как и в исходной сумме), поэтому 2S = 51·50, откуда S = 51 · 50 : 2 = 1275.
б) Решаем аналогично пункту а:
S = 10 + 11 + 12 + . + 99
S = 99 + 98 + 97 + . + 10
2S = 109 + 109 + 109 + . + 109
В последней сумме 90 слагаемых (именно столько существует двузначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 109·90, откуда S = 109 · 90 : 2 = 4905.
в) Решаем аналогично пунктам а и б:
S = 1000 + 1001 + 1002 + . + 9999
S = 9999 + 9998 + 9997 + . + 1000
2S = 1099 + 1099 + 1099 + . + 1099
В последней сумме 9000 слагаемых (именно столько существует четырёхзначных чисел и именно столько слагаемых в исходной сумме), поэтому 2S = 1099·9000, откуда S = 1099 · 9000 : 2 = 49495500.
Будем решать эту задачу по аналогии с задачей 1.
а) Обозначим искомую сумму S:
S = 1 + 3 + 5 + . + 99
S = 99 + 97 + 95 + . + 1
2S = 100 + 100 + 100 + . + 100
В последней сумме 50 слагаемых (как и в исходной сумме: среди 100 чисел от 1 до 100 ровно половина нечётных), поэтому 2S = 100·50, откуда S = 100 · 50 : 2 = 2500.
б) Решаем аналогично пункту а:
S = 3 + 6 + 9 + . + 150
S = 150 + 147 + 144 + . + 3
2S = 153 + 153 + 153 + . + 153
В последней сумме 150 : 3 = 50 слагаемых (как и в исходной сумме: среди 150 чисел от 1 до 150 ровно треть делится на 3), поэтому 2S = 153·50, откуда S = 153 · 50 : 2 = 3825.
в) Решаем аналогично пунктам а и б:
S = 1 + 7 + 13 + . + 79
S = 79 + 73 + 67 + . + 1
2S = 80 + 80 + 80 + . + 80
В последней сумме 14 слагаемых (как и в исходной сумме: неполные частные от деления этих чисел на 6 равны, соответственно, 0, 1, 2, . 13), поэтому 2S = 80·14, откуда S = 80 · 14 : 2 = 560.
Обратите внимание: поскольку 1 = 6·0 + 1, число 1 тоже делится на 6 с остатком 1 (и неполным частным 0).
Число клеток в k -м ряду фигуры равно k -му нечётному числу. Значит, площадь такой фигуры из n рядов равна сумме первых n нечётных чисел.
а) 1 + 3 + 5 + 7 + 9 = 25.
б) Двадцать пятое нечётное число — это число 49. Аналогично задаче 1 вычислим, что 1 + 3 + 5 + . + 49 = (1 + 49) · 25 : 2 = 25 2 = 625.
в) Заметим, что число клеток в такой фигуре всегда равно квадрату числа рядов. Это легче всего заметить геометрически (см. рисунок ниже).
Можно получить тот же результат и иначе. Заметим, что k -е нечётное число равно (2 k −1) (проверьте!). Таким образом, если фигура состоит из n рядов, число клеток в ней равно сумме нечётных чисел от 1 до (2 n −1). Вычислим эту сумму:
S = 1 + 3 + 5 + . + (2 n −1)
S = (2 n −1) + (2 n −3) + (2 n −5) + . + 1
2S = 2 n + 2 n + 2 n + . 2 n = 2 n · n
S = n · n = n 2 .
final: Последовательность Фибоначчи — такая последовательность натуральных чисел, в которой первые два числа — единицы, а каждое следующее число равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, 34, . .
а) Очевидно, что полоску 2×1 можно разрезать на доминошки одник способом, а полоску 2×2 — двумя. Далее, если от полоски 2×3 вначале отрезать одну вертикальную доминошку, останется полоска 2×2, которую можно разрезать одним из двух способов (как мы отметили выше). Если же от полоски 2×3 вначале отрезать две горизонтальные доминошки, останется прямоугольник 2×1, который можно разрезать одним способом. Итого полоску 2×3 можно разрезать 2 + 1 = 3 способами.
б) Аналогичным образом поступим с полоской 2×4. Либо мы сначала отрезаем одну вертикальную доминошку, и остаётся прямоугольник 2×3, который можно разрезать пятью способами, либо мы сначала отрезаем две горизонтальные доминошки, и остаётся прямоугольник 2×2, который можно разрезать тремя способами. Итого полоску 2×4 можно разрезать на доминошки 5 + 3 = 8 способами.
в)Рассуждая таким же образом, как в пунктах а и б, посчитаем, что полоску 2×5 можно разрезать 8 + 5 = 13 способами.
Докажем, что (число способов разрезать полоску 2×2013) = (число способов разрезать полоску 2×2012) + (число способов разрезать полоску 2×2011). В самом деле, если сначала отрезать от полоски 2×2013 одну вертикальную доминошку, останется полоска 2×2012, которую ещё надо разрезать; если же сначала отрезать две горизонтальные доминошки, останется разрезать полоску 2×2011. А из этого следует, что Даша и Таня в результате получили одно и то же число.
Вычислим сумму первых n подряд идущих натуральных чисел:
S = 1 + 2 + 3 + . + n
S = n + ( n −1) + ( n −2) + . + 1
2S = ( n +1) + ( n +1) + ( n +1) + . ( n +1) = n ·( n +1)
S = n ·( n +1) : 2.
Чтобы это число оканчивалось цифрой 7, вдвое большее число n ·( n +1) должно оканчиваться цифрой 4 (так как последняя цифра числа 2·7 = 14 равна 4). Последняя цифра произведения двух чисел равна последней цифре произведения их последних цифр (вспомните правило умножения в столбик). Пользуясь этим соображением, составим таблицу:
| Последняя цифра числа n | Последняя цифра числа ( n +1) | Последняя цифра числа n ·( n +1) |
| 0 | 1 | 0 |
| 1 | 2 | 2 |
| 2 | 3 | 6 |
| 3 | 4 | 2 |
| 4 | 5 | 0 |
| 5 | 6 | 0 |
| 6 | 7 | 2 |
| 7 | 8 | 6 |
| 8 | 9 | 2 |
| 9 | 0 | 0 |
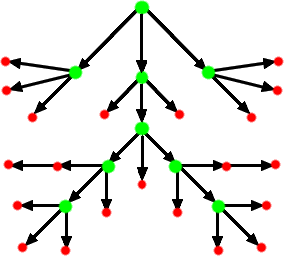
а) Обозначим через аn число способов подняться на лестницу из n ступенек, соблюдая условия задачи. Очевидно, a 1 = 1, a 2 = 2. Пусть Петя запрыгивает на лестницу из n > 2 ступенек. Если первый прыжок был на две ступеньки, то ему осталось запрыгнуть на ( n − 2) ступеньки, и число способов закончить подъем равно an −2. Если же первый прыжок был на одну ступеньку, то число способов закончить подъем равно an −1. Значит, an = an −1 + an −2. Поэтому числа an образуют последовательность Фибоначчи: a 3 = 3, a 4 = 5, a 5 = 8, a 6 = 13, a 7 = 21, a 8 = 34, a 9 = 55, a 10 = 89.
б) Каждую из 9 ступенек (кроме последней) Петя может либо перепрыгнуть, либо не перепрыгнуть независимо от того, на каких из верхних ступенек он останавливался. Поэтому количество способов спуститься по лестнице равно 2 9 = 512.
Источник