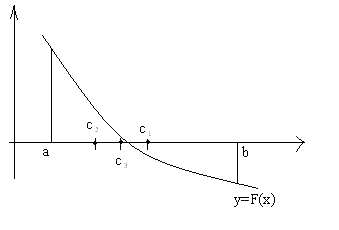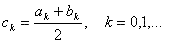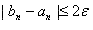- Вычислительная математика копия 1
- 1.1 Отделение корня
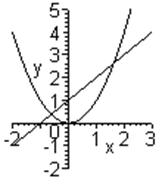
- Графический метод отделения корня
- 1.2 Уточнение корня методом деления отрезка пополам
- 1.3 Метод хорд
- Приближенное нахождение корней уравнения
- I. Графический способ отделения корней
- Графический способ отделения корней
- 1. Графический способ отделения корней
Вычислительная математика копия 1
Уравнение называется алгебраическим, если его можно представить в виде:
Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.
Решить уравнение означает найти такие значения x , при которых уравнение превращается в тождество.
Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.
1.1 Отделение корня
Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.
Отделить корень – значит указать такой отрезок [a , b] , на котором содержится ровно один корень уравнения f(x)=0.
Не существует алгоритмов отделения корня, пригодных для любых функций f (x). Если удастся подобрать такие a и b , что
2) f ( x ) – непрерывная на [ a , b ] функция (1.3)
3) f ( x ) – монотонная на [ a , b ] функция (1.4)
то можно утверждать, что на отрезке [a , b] корень отделен.
Условия (1.2) –(1.4) – достаточные условия того, что корень на [a , b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.
Корень можно отделить аналитически и графически.
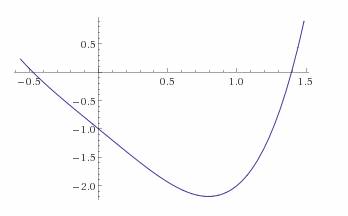
Пример. Аналитически отделить положительный корень уравнения x 3 -7x-5=0 Решение. Составим таблицу
Графический метод отделения корня
1.2 Уточнение корня методом деления отрезка пополам
Уточнить корень – значит найти его приближенное значение с заданной погрешностью e .
Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.
Предположим, что отрезок [a , b], на котором отделен корень уравнения, уже найден.
Пусть, например, f(a)> 0, f(b) e 1=(b-a)/2. Если эта погрешность не превышает некоторую заданную погрешность e , с которой нужно уточнить корень уравнения, то вычисления прекращаем и можно записать: ?=x ±(b-a)/2 . В противном случае определяем новый отрезок [a , b], на котором отделен корень нашего уравнения. Для этого определим знак функции в точке х. В нашем примере f (x )>0. Новый отрезок – отрезок [x , b], так как на концах этого отрезка функция имеет разные знаки. Переобозначим один из концов отрезка – в нашем случае положим a = x — и повторим процедуру для нового отрезка [a , b].
1.3 Метод хорд
Идея метода состоит в следующем. Проводим прямую через точки с координатами (a ,f(a)), (b ,f(b)). Находим точку пересечения прямой с осью Х. Определяем знак функции в этой точке. Далее проводим прямую через те точки, абсциссы которых содержат корень уравнения ? . Вычисления прекращаются, как только выполнится условие |xn+1-xn| e .
Источник
Приближенное нахождение корней уравнения
Задание 2 . 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.
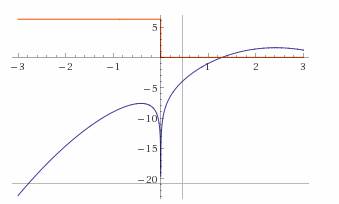
Пример №1 . Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать
Пример №2 . Определить и найти действительные корни с точностью до 0,001: а) x 4 – 2x – 1 = 0 — методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) — (x-2) 2 = 0 — методами: 1) хорд; 2) итераций.
Решение.
Найдем корни уравнения:
x 4 -2•x-1 = 0
Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h1 = -1 + 1*(2-(-1))/10 = -0.7
h2 = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4) 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 1.25 | 1.1 | 1.4 | -1.06 | -1.06 |
| 2 | 1.33 | 1.25 | 1.4 | -0.57 | -0.57 |
| 3 | 1.36 | 1.33 | 1.4 | -0.28 | -0.28 |
| 4 | 1.38 | 1.36 | 1.4 | -0.12 | -0.12 |
| 5 | 1.39 | 1.38 | 1.4 | -0.0415 | -0.0415 |
| 6 | 1.4 | 1.39 | 1.4 | -0.000217 | -0.000217 |
| 7 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0206 |
| 8 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0102 |
| 9 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.00498 |
Ответ:
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 — 1.4)/9 = 6.5E-5
Посмотрите как можно быстро решить задачу.
Источник
I. Графический способ отделения корней
Отделение корней
Постановка задачи
Решение уравнений с одной переменной
Рассмотрим уравнение вида F(x)=0, где F(x) – определенная и непрерывная на отрезке [a,b] функция.
Корнем уравнения F(x)=0 называется такое значение x * , которое обращает уравнение в верное равенство.
x * — корень уравнения F(x)=0 x * — нуль функции y=F(x).
Решить уравнение – значит установить, имеет ли оно корни, сколько корней, и найти их значения с заданной степенью точности.
Нахождение корней уравнения состоит из двух этапов:
I. Отделение корней – выделение промежутков, содержащих ровно 1 корень.
II. Уточнение корней – нахождение корней с заданной степенью точности.
Отделение корней может осуществляться графически или программным путем.
Если на отрезке [a,b] функция y=F(x) определена и непрерывна, и на его концах принимает значения разных знаков (т.е. F(a)F(b) 2 -x-1=0. Построим график функции y=x 2 -x-1 и укажем отрезки, содержащие точки пересечения графика функции с осью абсцисс.
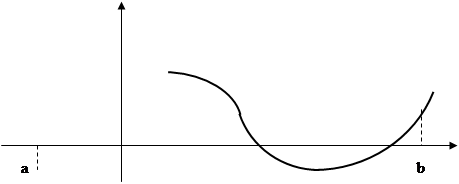
Искомые промежутки: [-1; 0] [1; 2].
б) Иногда проще рассмотреть вместо уравнения y=F(x) равносильное ему уравнение f1(x)=f2(x). В этом случае требуется указать отрезок, содержащий абсциссу точки пересечения графиков функций y=f1(x) и y=f2(x).
Например, пусть требуется отделить корни уравнения x 2 -x-1=0. Рассмотрим равносильное ему уравнение x 2 =x+1. Тогда вместо отрезков, содержащих точки пересечения графика функции y=x 2 -x-1 с осью абсцисс, можно указать отрезки, содержащие точки пересечения графиков функций f1(x)=x 2 и f2(x)=x+1.
Источник
Графический способ отделения корней
1. Графический способ отделения корней
Отделение корней во многих случая можно произвести графически, «учитывая что действительные корни уравнения F(x)=0 (1) — это есть точки пересечения графика функции y=F(x) с осью абсцисс y=0, нужно построить график функции y=F(x) на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y=F(x) исходное уравнение (1) заменяют равносильным ему уравнением f1(x)=f2(x) (2). Далее строятся графики функций y1=f1(x) и y2=f2(x) , а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков»[1].
На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2x)+x-5=0 графически на отрезке [-10;10], используя:
Построим график функции f(x)=cos(2x)+x-5 в декартовой системе координат. Для этого нужно:
Ввести в ячейку A1 текст х.
Ввести в ячейку B1 текст y=cos(2x)+x-5.
Ввести в ячейку А2 число -10, а в ячейку А3 число -9.
Выделить ячейки А2 и А3.
Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.
Ячейки автоматически заполняются цифрами :
Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.
Методом протягивания заполнить диапазон ячеек В3:В22.
Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».
Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.
Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.
В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».
Подписать названия осей x и y соответственно, нажать «далее».
Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».
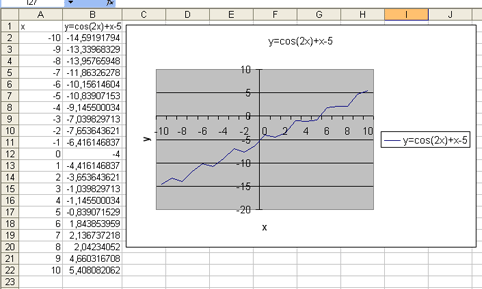
В итоге получаем следующее:
Анализируя полученное изображение графика, можно сказать, что уравнение cos(2x)+x-5=0 имеет один корень – это видно из пересечения графика функции y=cos(2x)+x-5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок изоляции.
Для подтверждения полученных данных, можно решить эту же задачу вторым способом, используя формулу (2). Для этого необходимо уравнение cos(2x)+x-5=0 преобразовать к виду: cos(2x)=5-x. Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y1=cos(2x) и y2=5-x. Для решения этой задачи в MS Excel необходимо выполнить следующие действия:
Вести в ячейки А1:C1 соответственно текст: «x», «y1=cos(2x)», «y2=5-x».
A2:A22 заполнить так же как при решении задачи первым способом.
В В2 ввести формулу =COS(2*A2).
Методом протягивания заполнить диапазон ячеек В3:В22.
В С2 ввести =5-A2.
Методом протягивания заполнить диапазон ячеек С3:С22.
С помощью Мастера диаграмм выбрать график (первый вид).
В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.
Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.
Подписать ось x , выбрав диапазон А2:А22.
Подписать соответственно оси x и y.
Поместить диаграмму на имеющемся листе.
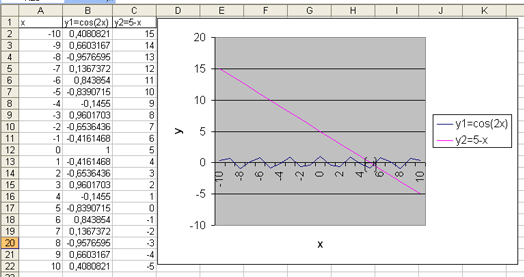
В итоге получаем следующее:
Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок изоляции [5;6], что и при решении задачи первым способом.
1. Метод половинного деления
Пусть корень уравнения (1) отделен на отрезке [a;b]. Требуется найти значение корня с точностью ε.
«Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности (6):
В в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которых функция F(x)=0 имеет разные знаки»[8]. «Точность будет достигнута, если:
Корень уравнения вычисляется по формуле x=(an+bn)/2 (7)»[1].
Пусть дана задача следующего характера: Уточнить корни уравнения cos(2x)+x-5=0 методом половинного деления с точностью до 0,00001, используя:
Для того чтобы уточнить корни уравнения cos(2x)+x-5=0 методом половинного деления, используя Excel, необходимо выполнить следующие действия:
Заполнить ячейки A1:H1 последовательно следующим образом: a, b, c=(a+b)/2, f(a), f(b), f(c), |b-a| Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
Источник
