Найти действительную величину четырехугольника способом перемены плоскостей проекций

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

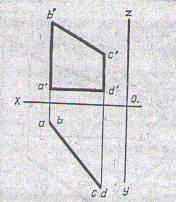
Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник

ПРАКТИЧЕСКИЕ ЗАНЯТИЯ №28 и №29

Тема: Определение действительной величины способом перемены плоскостей проекций. Определение действительной величины способом вращения

Цель работы: Знать способы определения действительной величины плоской фигуры. Уметь определять действительную величину плоской фигуры.

Порядок выполнения работы

1. По координатам вершин четырехугольника построить его комплексный чертеж (Задание 1).

2. Найти действительную величину четырехугольника способом вращения

3. Найти действительную величину четырехугольника способом перемены плоскостей проекций.

4. По координатам вершин А, В и С построить комплексный чертеж треугольника общего положения (Задание 2).

5. Найти действительную величину треугольника способом перемены плоскостей проекций.

6. Работу выполнить по своему варианту в тетради для практических занятий.

Задание для выполнения работы

X Y Z X Y Z X Y Z X Y Z 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 58 45 55 70 58 45 65 70 58 66 45 55 70 65 58 15 65 60 20 15 60 70 20 15 15 60 65 20 70 15 10 12 25 0 10 12 15 0 10 10 12 25 0 15 10 58 45 55 70 58 45 65 70 58 66 45 55 70 65 58 15 65 60 20 15 60 70 20 15 15 60 65 20 70 15 55 30 70 20 55 30 70 20 55 55 30 70 20 70 55 25 15 20 30 25 15 20 30 25 25 15 20 30 18 25 48 15 20 65 48 15 20 65 48 48 15 20 65 12 48 40 60 40 70 40 60 40 70 40 40 60 40 70 40 40 25 15 20 30 25 15 20 30 25 25 15 20 30 18 25 48 15 20 65 48 15 20 65 48 48 15 20 65 12 48 10 20 0 15 10 20 15 15 10 10 20 0 15 15 10 X Y Z X Y Z X Y Z 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 55 56 45 55 55 56 45 55 55 56 45 55 55 56 45 40 20 35 38 40 20 35 38 40 20 35 38 40 20 35 8 35 20 20 8 35 20 20 8 35 20 20 8 35 20 30 10 60 10 30 10 60 10 30 10 60 10 30 10 60 10 5 10 45 10 5 10 45 10 5 10 45 10 5 10 40 50 60 55 40 50 60 55 40 50 60 55 40 50 60 10 30 5 20 10 30 5 20 10 30 5 20 10 30 5 30 50 25 10 30 50 25 10 30 50 25 10 30 50 25 20 15 5 5 20 15 5 5 20 15 5 5 20 15 5

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №30

Тема: Выполнение аксонометрических проекций плоских фигур

Цель работы: Умение выполнять аксонометрические проекции плоских фигур в трех плоскостях проекций.

Порядок выполнения работы

1. Выполнить чертежи плоских фигур, изображенных на стр.32 [1].

2. На чертежах проставить размеры.

3. Выполнить изометрические проекции фигур в плоскостях H, V, W.

4. Работу выполнить на формате А-3.

Рекомендуемая литература

1. Исаев И.А. Инженерная графика: Рабочая тетрадь. Часть I. – М.: ФОРУМ,2012.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №31

Тема: Выполнение аксонометрических проекций окружности

Цель работы: Умение выполнять аксонометриию окружности в трех плоскостях проекций.

Порядок выполнения работы

1. Выполнить окружность произвольного радиуса, стр.31 [1].

2. Выполнить изометрические проекции окружности в плоскостях H, V, W.

3. Работу выполнить на формате А-4.

Рекомендуемая литература

1. Исаев И.А. Инженерная графика: Рабочая тетрадь. Часть I. – М.: ФОРУМ,2012.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №32

Тема: Проецирование многогранников с нанесением точек

На поверхность

Цель работы: Умение проецировать на три плоскости проекций призму и пирамиду и находить проекции точек на их поверхности.

Порядок выполнения работы

1. Построить в трех проекциях призму и пирамиду.

2. Найти проекции точек, расположенных: одна на ребре, вторая на грани.

3. Работу выполнить по своему варианту на формате А-4.

Задание для выполнения работы

Источник

Определение натуральной величины фигуры сечения

Нередко практический интерес представляет задача определения натуральной величины фигуры сечения.

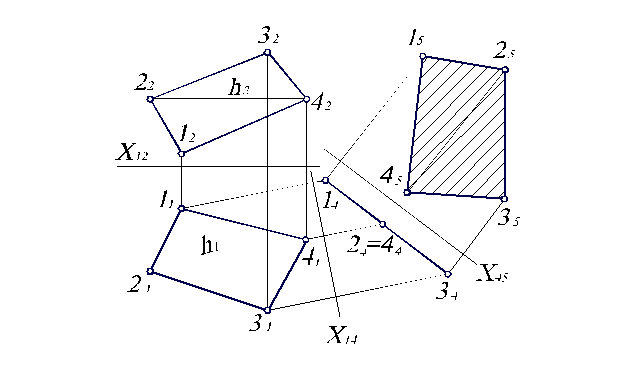
Определим натуральную величину сечения (четырехугольника), полученного на рис. 3.11. Так как четырехугольник 1234 занимает общее положение в пространстве, то его натуральную величину можно определить двумя переменами плоскостей проекций, сначала построив плоскость, перпендикулярную четырехугольнику 1234, а затем – параллельную ему. Чтобы не загромождать чертеж (рис. 3.11), вынесем построения на отдельный рисунок 3.12. Для построения плоскости, перпендикулярной плоскости четырехугольника 1234, необходимо начертить одну из главных линий, например, горизонталь. Ее фронтальная проекция h₂ должна быть параллельна оси П₁/П₂. По точкам пересечения 2 и 4 с четырехугольником 1234 находим и горизонтальную проекцию h₁ горизонтали.

Новая ось П₄/П₁, разделяющая П₁ и новую плоскость П₄, должна быть перпендикулярна h₁. Затем получаем проекцию 1₄2₄3₄4₄ в виде прямой. И наконец, вычертив вторую новую ось П₅/П₄, параллельно 1₄3₄, построим проекцию 1₅2₅3₅4₅ четырехугольника в плоскости П₅. Это и есть натуральная величина четырехугольника 1234. Сечение заштрихуем под углом 45° к горизонтальной прямой.

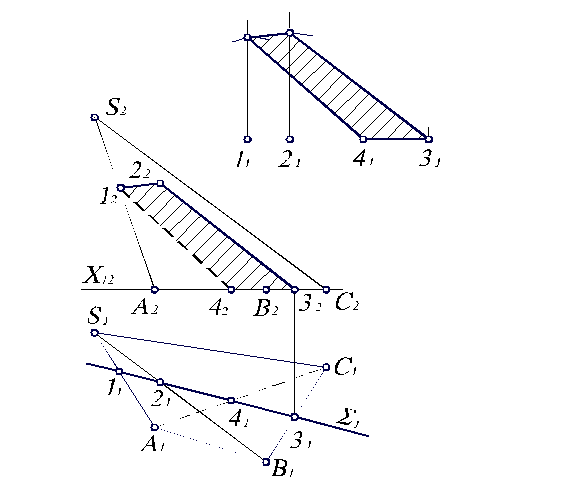
Чаще приходится решать более простую задачу – определение натуральной величины сечения многогранника плоскостью частного положения. В этом случае достаточно сделать всего одну замену плоскостей проекций. Рассмотрим на примере сечения пирамиды горизонтально–проецирующей плоскостью S (рис 3.13). Пусть задана горизонтальная проекция S₁. Необходимо найти линию пересечения плоскости S с пирамидой и определить натуральную величину сечения. Таким образом, задача разбивается на две части: сначала надо построить сечение в плоскостях П₁и П₂, а затем определить его натуральную величину.

Рис. 3.13. Построение линии пересечения и определение натуральной величины сечения пирамиды плоскостью.

Чтобы решить первую часть задачи нужно найти все точки пересечения плоскости S с ребрами пирамиды и соединить их отрезками прямой. Горизонтальная проекция S₁ пересекает ребра пирамиды в точках 1₁, 2₁, 3₁, 4₁ (рис. 3.13, а). По линиям связи находим их фронтальные проекции 1₂, 2₂, 3₂, 4₂ на фронтальных проекциях соответствующих ребер. Соединяя найденные точки, получаем линию пересечения 1₂2₂3₂4₂ заданной плоскости с пирамидой. Отрезок 1₂4₂ этой линии будет невидимым, так как он лежит на невидимой грани A₂S₂C₂. Плоская фигура, ограниченная полученной линией (на рис. 5.9, а заштрихована), и является сечением пирамиды плоскостью. В нашем примере это четырехугольник 1234.

Для определения натуральной величины четырехугольника 1234 способом замены плоскостей проекций не обязательно строить новую ось параллельно S₁ (или 1₁2₁4₁3₁), ввиду ограниченности площади чертежа. Достаточно соблюдать основные принципы построения. Начертим новую ось на свободном поле чертежа. Перенесем на нее точки 1₁,2₁,4₁,3₁, не меняя расстояния между ними. Проведем через них перпендикуляры к оси. Затем отложим на построенных перпендикулярах отрезки, равные расстояниям от оси П₂/П₁, которую считаем расположенной на основании А₂В₂С₂ пирамиды, до соответствующих проекций 1₂, 2₂, 4₂, 3₂. Соединив указанные точки, получим натуральную величину сечения пирамиды заданной плоскостью S (рис. 3.13, б).

Как видим, сечение в натуральную величину отличается от 1₂2₂3₂4₂ лишь тем, что оно вытянуто вдоль S₁.

Источник