Найти число способов распределения

тБУУНПФТЙН УМЕДХАЭЙЕ ЧПЪНПЦОЩЕ УРПУПВЩ ЧЩВПТБ.

1. чЩВПТ У ЧПЪЧТБЭЕОЙЕН: ЛБЦДЩК ЧЩОХФЩК ЫБТ ЧПЪЧТБЭБЕФУС Ч ХТОХ, ЛБЦДЩК УМЕДХАЭЙК ЫБТ ЧЩВЙТБЕФУС ЙЪ РПМОПК ХТОЩ. ч РПМХЮЕООПН ОБВПТЕ ЙЪ ОПНЕТПЧ ЫБТПЧ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ. 2. чЩВПТ ВЕЪ ЧПЪЧТБЭЕОЙС: ЧЩОХФЩЕ ЫБТЩ Ч ХТОХ ОЕ ЧПЪЧТБЭБАФУС, Й Ч РПМХЮЕООПН ОБВПТЕ ОЕ НПЗХФ ЧУФТЕЮБФШУС ПДОЙ Й ФЕ ЦЕ ОПНЕТБ.

хУМПЧЙНУС, ЛБЛЙЕ ТЕЪХМШФБФЩ ЧЩВПТБ (ОБВПТЩ ЙЪ ОПНЕТПЧ ЫБТПЧ) НЩ ВХДЕН УЮЙФБФШ ТБЪМЙЮОЩНЙ. еУФШ ТПЧОП ДЧЕ ЧПЪНПЦОПУФЙ.

1. чЩВПТ У ХЮЈФПН РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН ЙМЙ РПТСДЛПН ОПНЕТПЧ. фБЛ, РТЙ ЧЩВПТЕ ФТЈИ ЫБТПЧ ЙЪ ХТОЩ, УПДЕТЦБЭЕК 5 ЫБТПЧ, ОБВПТЩ (1, 5, 2), (2, 5, 1) Й (4, 4, 5) ТБЪМЙЮОЩ, ЕУМЙ РПТСДПЛ ХЮЙФЩЧБЕФУС. 2. чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ : ДЧБ ОБВПТБ ОПНЕТПЧ ЫБТПЧ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, ЕУМЙ ПОЙ ПФМЙЮБАФУС УПУФБЧПН. оБВПТЩ, ПФМЙЮБАЭЙЕУС МЙЫШ РПТСДЛПН УМЕДПЧБОЙС ОПНЕТПЧ, УЮЙФБАФУС ПДЙОБЛПЧЩНЙ.

фБЛ, ОБВПТЩ (1, 5, 2) Й (2, 5, 1) ОЕ ТБЪМЙЮБАФУС Й ПВТБЪХАФ ПДЙО Й ФПФ ЦЕ ТЕЪХМШФБФ ЧЩВПТБ, ЕУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБЕФУС.

рПДУЮЙФБЕН, УЛПМШЛП ЧПЪНПЦОП ТБЪМЙЮОЩИ ТЕЪХМШФБФПЧ ДМС ЛБЦДПК ЙЪ ЮЕФЩТЈИ УИЕН ЧЩВПТБ (ЧЩВПТ У ЧПЪЧТБЭЕОЙЕН ЙМЙ ВЕЪ, Й Ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ У ХЮЈФПН РПТСДЛБ ЙМЙ ВЕЪ).

Й ОБЪЩЧБЕФУС ЮЙУМПН ТБЪНЕЭЕОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.

ТБЧОП . дМС ЛБЦДПК ФБЛПК РБТЩ ЕУФШ УРПУПВБ ЧЩВТБФШ ФТЕФЙК ЫБТ. рП ФЕПТЕНЕ 1, ЮЙУМП ЧПЪНПЦОЩИ ФТПЕЛ

ТБЧОП РТПЙЪЧЕДЕОЙА ЮЙУМБ РБТ Й ЮЙУМБ УРПУПВПЧ ЧЩВПТБ ФТЕФШЕЗП ЫБТБ, Ф.Е. ТБЧОП . рТПДПМЦБС ТБУУХЦДЕОЙС, РПМХЮЙН, ЮФП ПВЭЕЕ ЮЙУМП ЧПЪНПЦОЩИ ОБВПТПЧ ЙЪ ЫБТПЧ ТБЧОП . ч ЬФПН РТПЙЪЧЕДЕОЙЙ УПНОПЦЙФЕМЕК РПУМЕДОЙК НОПЦЙФЕМШ ЕУФШ ЮЙУМП УРПУПВПЧ ЧЩВПТБ -ЗП ЫБТБ, ЛПЗДБ ХЦЕ ЧЩВТБОЩ РТЕДЩДХЭЙЕ.

Й ОБЪЩЧБЕФУС ЮЙУМПН УПЮЕФБОЙК ЙЪ ЬМЕНЕОФПЧ РП ЬМЕНЕОФПЧ.

У ХЮЈФПН РПТСДЛБ	ВЕЪ ХЮЈФБ РПТСДЛБ
(1,1)	(1,1)
(2,2)	(2,2)
(1,2) (2,1)	> (1,2)

чЙДЙН, ЮФП Ч УИЕНЕ «ВЕЪ ХЮЈФБ РПТСДЛБ» РПМХЮЙМПУШ ФТЙ ТБЪМЙЮОЩИ ТЕЪХМШФБФБ, Ч ПФМЙЮЙЕ ПФ ЮЕФЩТЈИ ТЕЪХМШФБФПЧ Ч УИЕНЕ «У ХЮЈФПН РПТСДЛБ». ъБНЕФЙН ФБЛЦЕ, ЮФП ОЙЛБЛЙН ДЕМЕОЙЕН ОБ «ЮЙУМП ЛБЛЙИ-ОЙВХДШ РЕТЕУФБОПЧПЛ», ЛПФПТПЕ РПНПЗМП ЙЪВБЧЙФШУС ПФ ХЮЈФБ РПТСДЛБ РТЙ ЧЩВПТЕ ВЕЪ ЧПЪЧТБЭЕОЙС, ЮЙУМП 3 ЙЪ ЮЙУМБ 4 РПМХЮЙФШ ОЕ ХДБУФУС.

рТЕДУФБЧЙН УЕВЕ ДТХЗПК ЬЛУРЕТЙНЕОФ, ЙНЕАЭЙК ФПЮОП ФБЛЙЕ ЦЕ ТЕЪХМШФБФЩ, Й РПУЮЙФБЕН ЙИ ЛПМЙЮЕУФЧП. еУФШ СЭЙЛПЧ, Ч ЛПФПТЩИ ТБЪНЕЭБАФУС ЫБТПЧ. оБУ ЙОФЕТЕУХЕФ ФПМШЛП ЮЙУМП ЫБТПЧ Ч ЛБЦДПН СЭЙЛЕ. тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ УОПЧБ СЧМСЕФУС ОБВПТ ЮЙУЕМ , ЗДЕ ТБЧОП ЮЙУМХ ЫБТПЧ Ч СЭЙЛЕ У ОПНЕТПН , Й . юЙУМБ РТЙОЙНБАФ ОБФХТБМШОЩЕ ЪОБЮЕОЙС ЙМЙ ТБЧОЩ ОХМА.

б ФЕРЕТШ ЙЪПВТБЪЙН ТЕЪХМШФБФ ФБЛПЗП ТБЪНЕЭЕОЙС Ч ЧЙДЕ УИЕНЩ, Ч ЛПФПТПК ЧЕТФЙЛБМШОЩЕ МЙОЙЙ ПВПЪОБЮБАФ РЕТЕЗПТПДЛЙ НЕЦДХ СЭЙЛБНЙ, Б ФПЮЛЙ ОБИПДСЭЙЕУС Ч СЭЙЛБИ ЫБТЩ:

нЩ ЧЙДЙН ТЕЪХМШФБФ ТБЪНЕЭЕОЙС ДЕЧСФЙ ЫБТПЧ РП УЕНЙ СЭЙЛБН. рЕТЧЩК СЭЙЛ УПДЕТЦЙФ ФТЙ ЫБТБ, ЧФПТПК Й ЫЕУФПК СЭЙЛЙ РХУФЩ, ФТЕФЙК СЭЙЛ УПДЕТЦЙФ ПДЙО ЫБТ, Ч ЮЕФЧЈТФПН Й РСФПН СЭЙЛБИ МЕЦЙФ РП ДЧБ ЫБТБ. рЕТЕМПЦЙН ПДЙО ЫБТ ЙЪ РЕТЧПЗП СЭЙЛБ ЧП ЧФПТПК Й ЙЪПВТБЪЙН ФБЛЙН ЦЕ ПВТБЪПН ЕЭЈ ДЧБ ТЕЪХМШФБФБ ТБЪНЕЭЕОЙС:

чЙДЙН, ЮФП ЧУЕ ТБЪНЕЭЕОЙС НПЦОП РПМХЮЙФШ, НЕОСС НЕЦДХ УПВПК ЫБТЩ Й РЕТЕЗПТПДЛЙ, ЙМЙ ТБУУФБЧМСС ЫБТПЧ ОБ НЕУФБИ. юЙУМП РПМХЮБЕФУС ФБЛ: Х СЭЙЛПЧ ЕУФШ ТПЧОП РЕТЕЗПТПДЛБ, УЮЙФБС ЛТБКОЙЕ, ОП ЙЪ ОЙИ РЕТЕНЕЭБФШ НПЦОП МЙЫШ ЧОХФТЕООАА РЕТЕЗПТПДЛХ. фБЛЙН ПВТБЪПН, ЙНЕЕФУС НЕУФ, ЛПФПТЩЕ НПЦОП ЪБОСФШ ЫБТБНЙ МЙВП ЧОХФТЕООЙНЙ РЕТЕЗПТПДЛБНЙ. рЕТЕВТБЧ ЧУЕ ЧПЪНПЦОЩЕ УРПУПВЩ ТБУУФБЧЙФШ ЫБТПЧ ОБ ЬФЙИ НЕУФБИ (ЪБРПМОСС ПУФБЧЫЙЕУС НЕУФБ РЕТЕЗПТПДЛБНЙ), РЕТЕВЕТЕН ЧУЕ ОХЦОЩЕ ТБЪНЕЭЕОЙС.

пУФБМПУШ ЪБНЕФЙФШ, ЮФП УРПУПВПЧ ТБУУФБЧЙФШ ЫБТПЧ ОБ НЕУФБИ УХЭЕУФЧХЕФ

йНЕООП УФПМШЛП ЕУФШ УРПУПВПЧ ЧЩВТБФШ ЙЪ ОПНЕТПЧ НЕУФ ОПНЕТПЧ НЕУФ ДМС ЫБТПЧ.

Источник

Формулы: законы распределения случайных величин

В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.

Каталог формул по теории вероятности онлайн

Законы распределения на этой странице

Дискретные случайные величины

Биномиальное распределение ДСВ

Пусть дискретная случайная величина $X$ — количество «успехов» в последовательности из $n$ независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна $p$ («неуспеха» — $q=1-p$).

Закон распределения $X$ имеет вид:

$x_k$	0	1	.	k	.	n
$p_k$	$q^n$	$n\cdot p \cdot q^$	$C_n^k \cdot p^k \cdot q^$	$p^n$

Здесь вероятности находятся по формуле Бернулли:

$$ P(X=k) = C_n^k \cdot p^k \cdot (1-p)^ = C_n^k \cdot p^k \cdot q^, k=0,1,2. n. $$

Числовые характеристики биномиального распределения:

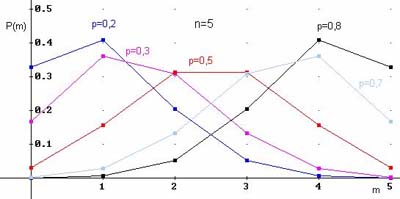
Примеры многоугольников распределения для $n=5$ и различных вероятностей:

Пуассоновское распределение ДСВ

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

При условии $p\to 0$, $n \to \infty$, $np \to \lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Ряд распределения по закону Пуассона имеет вид:

$x_k$	0	1	.	k	.
$p_k$	$e^<-\lambda>$	$\lambda e^<-\lambda>$	.	$\frac<\lambda^k>\cdot e^<-\lambda>$	.

Вероятности вычисляются по формуле Пуассона:

Числовые характеристики для распределения Пуассона:

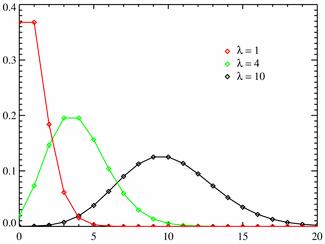
Разные многоугольники распределения при $\lambda = 1; 4; 10$.

Геометрическое распределение ДСВ

Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ — количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.

Формула для вероятностей:

$$ P(X=k) = q^k \cdot p, k=0,1,2. n. $$

Ряд распределения геометрического закона:

$x_k$	0	1	2	.	k	.
$p_k$	$p$	$q\cdot p$	$q^2 \cdot p$	.	$q^k \cdot p$	.

Гипергеометрическое распределение ДСВ

Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n \le N$). Найти закон распределения случайной величины $X$ — равной числу белых шаров среди выбранных.

Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n \lt K$, то до $n$). Вероятности вычисляются по формуле: $$ P(X=k)=\frac^>, \quad 0\le k \le K. $$

$$M(X)=\frac\cdot n, \quad D(X)=\frac\cdot n \cdot \frac \cdot \frac.$$

Непрерывные случайные величины

Показательное распределение НСВ

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Плотность распределения величины $X$(везде $ \lambda \gt 0)$:

Функция распределения величины $X$:

Числовые характеристики можно найти по формулам:

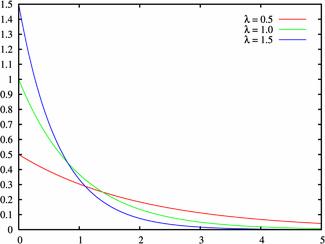
Плотность распределения при различных значениях $\lambda \gt 0$:

Равномерное распределение НСВ

Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.

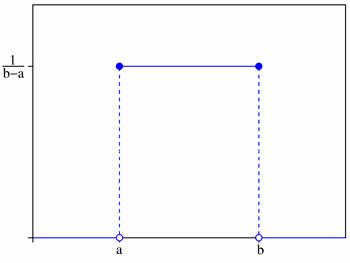
Плотность распределения на отрезке $(a;b)$:

$$ f(x)= \left\< \begin 0,\ x \le a\\ \frac <1>,\ a \lt x \le b, \\ 0,\ x \gt b, \\ \end \right. $$

$$ F(x)= \left\< \begin 0,\ x \le a\\ \frac ,\ a \lt x \le b, \\ 1,\ x \gt b, \\ \end \right. $$

Числовые характеристики равномерно распределенной случайной величины:

График плотности вероятностей:

Нормальное распределение или распределение Гаусса НСВ

Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.

Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Плотность распределения нормальной случайной величины $X$ имеет вид:

При $a=0$ и $\sigma=1$ эта функция принимает вид:

Числовые характеристики для нормального распределения:

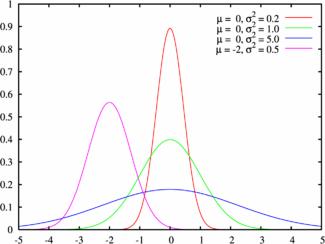
Пример графика плотности распределения для различных значений среднего и СКО:

Нормальный закон распределения случайной величины с параметрами $a=0$ и $\sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.

Функция Лапласа определяется как:

Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(\alpha, \beta)$:

$$ P(\alpha \lt X \lt \beta) = \Phi\left( \frac<\beta-a> <\sigma>\right) — \Phi\left( \frac<\alpha-a> <\sigma>\right). $$

Вероятность отклонения нормально распределенной случайной величины $X$ на величину $\delta$ от математического ожидания (по модулю).

Решенные задачи по теории вероятностей

Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:

Источник

Типичные распределения вероятности: шпаргалка data scientist-а

У data scientist-ов сотни распределений вероятности на любой вкус. С чего начать?

Data science, чем бы она там не была – та ещё штука. От какого-нибудь гуру на ваших сходках или хакатонах можно услышать:«Data scientist разбирается в статистике лучше, чем любой программист». Прикладные математики так мстят за то, что статистика уже не так на слуху, как в золотые 20е. У них даже по этому поводу есть своя несмешная диаграмма Венна. И вот, значит, внезапно вы, программист, оказываетесь совершенно не у дел в беседе о доверительных интервалах, вместо того, чтобы привычно ворчать на аналитиков, которые никогда не слышали о проекте Apache Bikeshed, чтобы распределённо форматировать комментарии. Для такой ситуации, чтобы быть в струе и снова стать душой компании – вам нужен экспресс-курс по статистике. Может, не достаточно глубокий, чтобы вы всё понимали, но вполне достаточный, чтобы так могло показаться на первый взгляд.

Вероятностные распределения – это основа статистики, так же как структуры данных – основа computer science. Если хотите говорить языком data scientist-а – надо начинать с их изучения. В принципе можно, если повезёт, делать простые анализы, используя R или scikit-learn вообще без понимания распределений, так же как можно написать программу на Java без понимания хэшфункций. Но рано или поздно это закончится слезами, ошибками, ложными результатами или — гораздо хуже – охами и выпученными глазами от старших статистиков.

Существуют сотни различных распределений, некоторые из которых на слух звучат как чудовища средневековых легенд, типа Muth или Lomax. Тем не менее, на практике более-менее часто используются около 15. Каковы они, и какие умные фразы о них требуется запомнить?

Итак, что такое распределение вероятности?

Всё время что-то происходит: кидаются кубики, идёт дождь, подъезжают автобусы. После того, как это что-то произошло, можно быть уверенным в некотором исходе: кубики выпали на 3 и 4, выпало 2.5 см дождя, автобус подъехал через 3 минуты. Но до этого момента мы можем говорить только о том, насколько каждый исход возможен. Распределения вероятности описывают то, как мы видим вероятность каждого исхода, что, зачастую, гораздо интереснее, чем знать только один, наиболее возможный, исход. Распределения бывают разных форм, но строго одного размера: сумма всех вероятностей в распределении — всегда 1.

Например, подбрасывание правильной монетки имеет два исхода: она упадёт либо орлом, либо решкой (предполагая, что она не приземлится на ребро и её не стащит в воздухе чайка). Перед броском мы верим, что с шансом 1 к 2 или с вероятностью 0.5 она упадёт орлом. Точно так же, как и решкой. Это распределение вероятности двух исходов броска, и, если вы внимательно прочитали это предложение, то вы уже поняли распределение Бернулли.

Несмотря на экзотические названия, распространённые распределения связаны друг с другом достаточно интуитивными и интересными способами, позволяющими легко их вспоминать и уверенно о них рассуждать. Некоторые естественно следуют, например, из распределения Бернулли. Время показать карту этих связей.

Каждое распределение иллюстрируется примером её функции плотности распределения (ФПР). Эта статья только о тех распределениях, у которых исходы – одиночные числа. Поэтому, горизонтальная ось каждого графика – набор возможных чисел-исходов. Вертикальная – вероятность каждого исхода. Некоторые распределения дискретны — у них исходы должны быть целыми числами, типа 0 или 5. Таковые обозначаются редкими линиями, по одной на каждый исход, с высотой, соответствующей вероятности данного исхода. Некоторые – непрерывны, у них исходы могут принять любое численное значение, типа -1.32 или 0.005. Эти показаны плотными кривыми с областями под секциями кривой, которые дают вероятности. Сумма высот линий и областей под кривыми — всегда 1.

Распечатайте, отрежьте по пунктирной линии и носите с собой в кошельке. Это — ваш путеводитель в стране распределений и их родственников.

Бернулли и равномерное

Вы уже встретились с распределением Бернулли выше, с двумя исходами – орлом или решкой. Представьте его теперь как распределение над 0 и 1, 0 – орёл, 1 – решка. Как уже понятно, оба исхода равновероятны, и это отражено на диаграмме. ФПР Бернулли содержит две линии одинаковой высоты, представляющие 2 равновероятных исхода: 0 и 1 соответственно.

Распределение Бернулли может представлять и неравновероятные исходы, типа броска неправильной монетки. Тогда вероятность орла будет не 0.5, а какая-то другая величина p, а вероятность решки – 1-p. Как и многие другие распределения, это на самом деле целое семейство распределений, задаваемых определёнными параметрами, как p выше. Когда будете думать «Бернулли» – думайте про «бросок (возможно, неправильной) монетки».

Отсюда весьма небольшой шаг до того, чтобы представить распределение поверх нескольких равновероятных исходов: равномерное распределение, характеризуемое плоской ФПР. Представьте правильный игральный кубик. Его исходы 1-6 равновероятны. Его можно задать для любого количества исходов n, и даже в виде непрерывного распределения.

Думайте о равномерном распределении как о «правильном игральном кубике».

Биномиальное и гипергеометрическое

Биномиальное распределение можно представить как сумму исходов тех вещей, которые следуют распределению Бернулли.

Киньте честную монету два раза – сколько раз будет орёл? Это число, подчиняющееся биномиальному распределению. Его параметры – n, число испытаний, и p – вероятность «успеха» (в нашем случае – орла или 1). Каждый бросок – распределённый по Бернулли исход, или испытание. Используйте биномиальное распределение, когда считаете количество успехов в вещах типа броска монеты, где каждый бросок не зависит от других и имеет одинаковую вероятность успеха.

Или представьте урну с одинаковым количество белых и чёрных шаров. Закройте глаза, вытащите шар, запишите его цвет и верните назад. Повторите. Сколько раз вытащился чёрный шар? Это число также подчиняется биномиальному распределению.

Эту странную ситуацию мы представили, чтобы было легче понять смысл гипергеометрического распределения. Это распределение того же числа, но в ситуации если бы мы не возвращали шары обратно. Оно, безусловно, двоюродный брат биномиального распределения, но не такое же, так как вероятность успеха изменяется с каждым вытащенным шаром. Если количество шаров достаточно велико по сравнению с количеством вытаскиваний – то эти распределения практически одинаковы, так как шанс успеха изменяется с каждым вытаскиванием крайне незначительно.

Когда где-то говорят о вытаскивании шаров из урн без возврата, практически всегда безопасно ввернуть «да, гипергеометрическое распределение», потому что в жизни я ещё не встречал никого, кто реально наполнял бы урны шарами и потом вытаскивал их и возвращал, или наоборот. У меня даже знакомых нет с урнами. Ещё чаще это распределение должно всплывать при выборе значимого подмножества некоторой генеральной совокупности в качестве выборки.

Тут может быть не очень понятно, а раз туториал и экспресс-курс для новичков — надо бы разъяснить. Генеральная совокупность — есть нечто, что мы хотим статистически оценить. Для оценки мы выбираем некоторую часть (подмножество) и производим требуемую оценку на ней (тогда это подмножество называется выборкой), предполагая, что для всей совокупности оценка будет похожей. Но чтобы это было верно, часто требуются дополнительные ограничения на определение подмножества выборки (или наоборот, по известной выборке нам надо оценить, описывает ли она достаточно точно совокупность).

Практический пример — нам нужно выбрать от компании в 100 человек представителей для поездки на E3. Известно, что в ней 10 человек уже ездили в прошлом году (но никто не признаётся). Сколько минимум нужно взять, чтобы в группе с большой вероятностью оказался хотя бы один опытный товарищ? В данном случае генеральная совокупность — 100, выборка — 10, требования к выборке — хотя бы один, уже ездивший на E3.

В википедии есть менее забавный, но более практичный пример про бракованные детали в партии.

Пуассон

Что насчёт количества заказчиков, звонящих по горячей линии в техподдержку каждую минуту? Это исход, чьё распределение на первый взгляд биномиальное, если считать каждую секунду как испытание Бернулли, в течение которой заказчик либо не позвонит (0), либо позвонит (1). Но электроснабжающие организации прекрасно знают: когда выключают электричество – за секунду могут позвонить двое или даже больше сотни людей. Представить это как 60000 миллисекундных испытаний тоже не поможет – испытаний больше, вероятность звонка в миллисекунду меньше, даже если не учитывать двух и более одновременно, но, технически – это всё ещё не испытание Бернулли. Тем не менее, срабатывает логическое рассуждение с переходом к бесконечности. Пусть n стремится к бесконечности, а p – к 0, и так, чтобы np было постоянным. Это как делить на всё более малые доли времени со всё менее малой вероятностью звонка. В пределе мы получим распределение Пуассона.

Так же, как и биномиальное, распределение Пуассона – это распределение количества: количества раз того, как что-то произойдёт. Оно параметризуется не вероятностью p и количеством испытаний n, но средней интенсивностью λ, что, в аналогии с биномиальным, просто постоянное значение np. Распределение Пуассона – то, о чём надо вспоминать, когда идёт речь о подсчёте событий за определённое время при постоянной заданной интенсивности.

Когда есть что-то, типа прихода пакетов на роутер или появления покупателей в магазине или что-то, ожидающее в очереди – думайте «Пуассон».

Геометрическое и отрицательное биномиальное

Из простых испытаний Бернулли появляется другое распределение. Сколько раз монетка выпадет решкой, прежде, чем выпасть орлом? Число решек подчиняется геометрическому распределению. Как и распределение Бернулли, оно параметризуется вероятностью успешного исхода, p. Оно не параметризуется числом n, количеством бросков-испытаний, потому что число неудачных испытаний как раз и есть исход.

Если биномиальное распределение это «сколько успехов», то геометрическое это «Сколько неудач до успеха?».

Отрицательное биномиальное распределение – простое обобщение предыдущего. Это количество неудач до того, как будет r, а не 1, успехов. Поэтому оно дополнительно параметризуется этим r. Иногда его описывают как число успехов до r неудач. Но, как говорит мой лайф-коуч: «Ты сам решаешь, что есть успех, а что — неудача», так что это тоже самое, если при этом не забыть, что вероятность p тоже должна правильной вероятностью успеха или неудачи соответственно.

Если нужна будет шутка для снятия напряжения, можно упомянуть, что биномиальное и гипергеометрическое распределение – это очевидная пара, но и геометрическое и отрицательное биномиальное так же весьма похожи, после чего заявить «Ну и кто же так их все называет, а?»

Экспоненциальное и Вейбула

Снова о звонках в техподдержку: сколько пройдёт до следующего звонка? Распределение этого времени ожидания как будто бы геометрическое, потому что каждая секунда, пока никто не звонит – это как неуспех, до секунды, пока, наконец, звонок не произойдёт. Количество неудач –это как количество секунд, пока никто не звонил, и это практически время до следующего звонка, но «практически» нам недостаточно. Суть в том, что это время будет суммой целых секунд, и, таким образом, не получится посчитать ожидание внутри этой секунды до непосредственно звонка.

Ну и, как и раньше, переходим в геометрическом распределении к пределу, относительно временных долей – и вуаля. Получаем экспоненциальное распределение, которое точно описывает время до звонка. Это непрерывное распределение, первое такое у нас, потому что исход не обязательно в целых секундах. Как и распределение Пуассона, оно параметризуется интенсивностью λ.

Повторяя связь биномиального с геометрическим, Пуассоновское «сколько событий за время?» связано с экспоненциальным «сколько до события?». Если есть события, количество которых на единицу времени подчиняется распределению Пуассона, то время между ними подчиняется экспоненциальному распределению с тем же параметром λ. Это соответствие между двумя распределениями необходимо отмечать, когда обсуждается любое из них.

Экспоненциальное распределение должно приходить на ум при размышлении о «времени до события», возможно, «времени до отказа». По факту, это такая важная ситуация, что существуют более обобщённые распределения чтобы описать наработку-на-отказ, типа распределения Вейбула. В то время, как экспоненциальное распределение подходит, когда интенсивность — износа, или отказов, например – постоянна, распределение Вейбула может моделировать увеличивающуюся (или уменьшающуюся) со временем интенсивность отказов. Экспоненциальное, в общем-то, частный случай.

Думайте «Вейбул» когда разговор заходит о наработке-на-отказ.

Нормальное, логнормальное, Стьюдента и хи-квадрат

Нормальное, или гауссово, распределение, наверное, одно из важнейших. Его колоколообразная форма узнаётся сразу. Как и e, это особенно любопытная сущность, которая проявляется везде, даже из внешне самых простых источников. Возьмите набор значений, подчиняющихся одному распределению – любому! – и сложите их. Распределение их суммы подчиняется (приблизительно) нормальному распределению. Чем больше вещей суммируется – тем ближе их сумма соответствует нормальному распределению (подвох: распределение слагаемых должно быть предсказуемым, быть независимым, оно стремится только к нормальному). То, что это так, несмотря на исходное распределение – это потрясающе.

Меня удивило, что автор не пишет про необходимость сопоставимого масштаба суммируемых распределений: если одно существенно доминирует надо остальными — сходиться будет крайне плохо. И, в общем-то, абсолютная взаимная независимость необязательна, достаточна слабая зависимость.

Ну сойдёт, наверное, для вечеринок, как он написал.

Это называется «центральная предельная теорема», и надо знать, что это, почему так названо и что означает, иначе моментально засмеют.

В её разрезе, нормальное связано со всеми распределениями. Хотя, в основном, его связывают с распределениями всяких сумм. Сумма испытаний Бернулли следует биномиальному распределению и, с увеличением количества испытаний, это биномиальное распределение становится всё ближе в нормальному распределению. Аналогично и его двоюродный брат – гипергеометрическое распределение. Распределение Пуассона – предельная форма биномиального – так же приближается к нормальному с увеличением параметра интенсивности.

Исходы, которые подчиняются логнормальному распределению, дают значения, логарифм которых нормально распределён. Или по-другому: экспонента нормально распределённого значения логнормально распределена. Если суммы – нормально распределены, то запомните так же, что произведения распределены логнормально.

t-Распределение Стьюдента – это основа t-теста, который многие нестатистики изучают в других областях. Оно используется для предположений о среднем нормального распределения и так же стремится к нормальному распределению с увеличением своего параметра. Отличительная особенность t-распределения – его хвосты, которые толще, чем у нормального распределения.

Если толстохвостый анекдот недостаточно раскачал вашего соседа – переходите в довольно забавной байке про пиво. Больше 100 лет назад Гиннесс использовал статистику, чтобы улучшить свой стаут. Тогда Вильям Сили Госсет и изобрёл полностью новую статистическую теорию для улучшенного выращивания ячменя. Госсет убедил босса, что другие пивовары не поймут, как использовать его идеи, и получил разрешение на публикацию, но под псевдонимом «Стьюдент». Самое известное достижение Госсета – как раз это самое t-распределение, которое, можно сказать, названо в честь него.

Наконец, распределение хи-квадрат – распределение сумм квадратов нормально-распределенных величин. На этом распределении построен тест хи-квадрат, который сам основан на сумме квадратов разниц, которые должны быть нормально распределены.

Гамма и бета

В этом месте, если вы уже заговорили о чём-то хи-квадратном, разговор начинается всерьёз. Вы уже, возможно, говорите с настоящими статистиками, и, наверное, стоит уже откланиваться, поскольку могут всплыть вещи типа гамма-распределения. Это обобщение и экспоненциального, и хи-квадрат распределения. Как и экспоненциальное распределение, оно используется для сложных моделей времен ожидания. Например, гамма-распределение появляется, когда моделируется время до следующих n событий. Оно появляется в машинном обучении как «сопряжённое априорное распределение» к парочке других распределений.

Не вступайте в разговор об этих сопряжённых распределениях, но если всё-таки придётся, не забудьте сказать о бета-распределении, потому что оно сопряжённое априорное к большинству упомянутых здесь распределений. Data-scientist-ы уверены, что оно именно для этого и сделано. Упомяните об этом ненароком и идите к двери.

Начало мудрости

Распределения вероятности — это то, о чём нельзя знать слишком много. По настоящему заинтересованные могут обратиться к этой супердетализированной карте всех распределений вероятности. Надеюсь, этот шуточный путеводитель даст вам уверенность казаться «в теме» в современной технокультуре. Или, по крайней мере, способ с высокой вероятностью определить, когда надо идти на менее ботанскую вечеринку.

Шон Овен – директор Data Science в Cloudera, Лондон. До Клаудеры он основал Myrrix Ltd. (сейчас проект Oryx) для коммерционализации широкомасштабных рекомендательных систем в реальном времени на Hadoop. Он так же контрибьютор Apache Spark и соавтор O’Reilly Media’s Advanced Analytics with Spark

Источник