Найдите количество способов закрасить некоторые клетки лесенки

Разбор олимпиадной задачи — Лесенка

Задача взята с acmp.ru (Время: 1 сек. Память: 16 Мб Сложность: 55%)

Очень хорошая задача на понимание рекурсии, рекомендую.

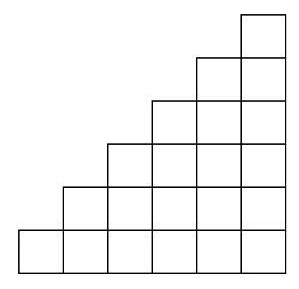
Лесенкой называется набор кубиков, в котором каждый более верхний слой содержит кубиков меньше, чем предыдущий. Требуется написать программу, вычисляющую число лесенок, которое можно построить из N кубиков.

Входные данные:
Во входном файле INPUT.TXT записано натуральное число N (1 ≤ N ≤ 100) – количество кубиков в лесенке.

Выходные данные:
В выходной файл OUTPUT.TXT необходимо вывести число лесенок, которые можно построить из N кубиков.

Для начала, предлагаю попробовать вручную построить лесенки. В частности для второго примера:

Программа должна генерировать лесенки по определенному алгоритму, чтобы его лучше понять, предлагаю посмотреть на следующую картинку, где показано как из одной лесенки программа может получить другую:

Есть у нас лесенка из 7 кубиков, сложенных в ряд. В следующий ряд мы можем положить 1, 2 и 3 кубика. 4 кубика переложить уже нельзя, т.к. тогда в первом будет меньше чем во втором. Дальше аналогичным образом обрабатывается второй ряд, третий, четвертый и т.д. Т.е. налицо рекурсивный алгоритм.

Первый вариант решения (не пройдет все тесты) мог бы выглядеть так:

В функции main выполняется генерация кубиков в первом уровне. В нем может быть от 1 до n кубиков. Этот код вынесен в main потому что остальные уровни генерируются чуть-чуть иначе, в них должно учитываться число кубиков на предыдущем уровне (для первого уровня нет предыдущего).

Функция get_count возвращает единицу (лесенку удалось сгенерировать) если количество кубиков равно нулю — т.е. мы каким то корректным образом строили лесенку и у нас кончились кубики. Для остальных случаев мы запускаем рекурсивную функцию с различными наборами данных, уменьшая количество кубиков на текущем уровне и увеличивая на следующем.

Этот код будет работать корректно, но долго (не пройдет тесты по времени). Чтобы найти проблемное место можно заставить функцию get_count перед своим завершением выводить входные данные и результат (count) в файл или на экран. Мы увидим, что она много раз вызывается для отрицательных значений количества кубиков на уровне (n). Необходимо добавить проверку, что n — level больше ноля.

В последнем варианте программы убран также цикл из функции main. В самом деле, можно обобщить генерацию первого и последующих уровней если предположить что перед первым есть «нулевой», на котором находится n+1 кубик (заведомо шире любой лесенки из n кубиков).

Источник

Олимпиадные задания по математике

Решение №1567 Точка M – середина стороны AC равностороннего треугольника ABC.

Точка M — середина стороны AC равностороннего треугольника ABC. Точки P и R на отрезках AM и BC соответственно выбраны так, что AP = BR. Найдите сумму углов ARM, PBM и BMR.

• Запись опубликована: 06.02.2021
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №1356 Натуральное число, большее 1000000, даёт одинаковые остатки при делении на 40 и на 125.

Натуральное число, большее 1000000, даёт одинаковые остатки при делении на 40 и на 125. Какая цифра может стоять у этого числа в разряде сотен?

• Запись опубликована: 06.02.2021
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №1346 Шесть отшельников отправляются в паломничество. У каждого из них по шесть посохов …

Шесть отшельников отправляются в паломничество. У каждого из них по шесть посохов, а на каждом посохе – по шесть сучков. На каждом сучке висит по 6 котомок, в каждой котомке по шесть хлебов. В каждом хлебе по шесть скворцов. Сколько всего скворцов?

• Запись опубликована: 02.02.2021
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №1077 Петя выписал на доску пятизначное число, которое делится на 99.

Петя выписал на доску пятизначное число, которое делится на 99. А Вася смог вычеркнуть из этого числа одну цифру так, что получившееся четырёхзначное число тоже делится на 99. Приведите пример числа, которое мог выписать Петя, и укажите, какую цифру в нём мог вычеркнуть Вася.

• Запись опубликована: 22.11.2020
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №966 В 8:00 рейсовый автобус выехал из города А и поехал в сторону города Б со скоростью 64 км/ч.

В 8:00 рейсовый автобус выехал из города А и поехал в сторону города Б со скоростью 64 км/ч. Доехав до города Б, он сразу же развернулся и поехал обратно. В 12:30 автобусу оставалось 14 км до города А. Сколько километров от одного города до другого? (Всё время движения автобус ехал с постоянной скоростью.)

• Запись опубликована: 22.10.2020
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №965 Высота красного кубика составляет 2 см, высота синего кубика – 3 см, зелёного кубика – 4 см …

Высота красного кубика составляет 2 см, высота синего кубика — 3 см, зелёного кубика — 4 см. Петя построил из 8 кубиков башенку высоты 23 см. Какое наибольшее количество зеленых кубиков могло быть использовано при строительстве башенки?

• Запись опубликована: 22.10.2020
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №964 Женя сложил из пяти одинаковых прямоугольников фигуру и измерил длины трёх отрезков …

Женя сложил из пяти одинаковых прямоугольников фигуру и измерил длины трёх отрезков (см. рисунок). Чему равен периметр фигуры?

• Запись опубликована: 22.10.2020
• Рубрика записиОлимпиадные задания по математике
• Комментарии к записи:0 комментариев

Решение №963 Найдите количество способов закрасить некоторые клетки «лесенки» …

Найдите количество способов закрасить некоторые клетки «лесенки» так, чтобы выполнялись следующие условия: Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены. В одном столбце закрашено 5 клеток, в другом — 4 клетки, в третьем — 3 клетки, …, в последнем — 0 клеток.

Источник

Решение №963 Найдите количество способов закрасить некоторые клетки «лесенки» …

Найдите количество способов закрасить некоторые клетки «лесенки» так, чтобы выполнялись следующие условия:

• Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены.

• В одном столбце закрашено 5 клеток, в другом – 4 клетки, в третьем – 3 клетки, …, в последнем – 0 клеток.

Источник задания: ВсОШ sochisirius.ru

Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены.

Это условие говорит о том, что нужно начинать закрашивать клетки с нижний и подряд, не пропуская клеток.

5 клеток можем закрасить, только в 2 столбцах на выбор.
4 клетки, учитывая что в одном уже закрашено 5 клеток, можем тоже закрасить в 2 столбцах на выбор.
3 клетки, учитывая, что есть столбец с 5 клетками и 4 клетками, тоже 2 способами. И так далее..
2 клетки – 2 способами.
1 клетку – 2 способами.
0 клеток – 1 способом (останется один столбец)

Тогда всего вариантов:

2·2·2·2·2·1 = 32

Ответ: 32.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.8 / 5. Количество оценок: 6

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Источник

Найдите количество закрасить некоторые клетки «лесенки» так, чтобы выполнялись следующие условия: Ниже каждой закрашенной клетки либо нет других клеток, либо они все закрашены. В одном столбце закрашено 5 клеток, в другом — 4 клетки, в третьем — 3 клетки, …, в последнем — 0 клеток.

1)мы узнаем сколько осталось товара после первого дня:

2) мы узнаем сколько осталось товара после второго дня:

пусть 80% это весь товар во второй день, из этого следует что 80%=100%

где 100% товар второго дня

80%/100%*60%=48%-сколько продал магазин за втрой днеь

3)узнаем сколько процентов товара продал магазин за два дня:

витя придумал 6 выражений со скобками, значения которых равно 15, а лена придумала на 2 выражения больше. сколько всего выражений придумали лена и

витя — 6 в.лена — ? в., на 2 в. > , чем витя (стрелка от лены до вити)сколько всего выражений придумали лена и витя? решение: 1) 6+2=8 (в.) — придумала лена.2) 6+8=14 (в.) — придумали лена и витя.ответ: 14 выражений придумали лена и витя.витя придумал 6 выражений со скобками, значения которых равно 15, а лена придумала на 2 выражения больше. сколько всего выражений придумали лена и витя? какова сумма значений?

витя — 6 в.лена — ? в., на 2 в. > , чем витя (стрелка от лены до вити)сколько всего выражений придумали лена и витя? какова сумма значений? решение: 1) 6+2=8 (в.) — придумала лена.2) 6+8=14 (в.) — придумали лена и витя.3) 14·15=210 — значение всех выражений. ответ: 14 выражений придумали лена и витя; 210 значение всех выражений.

можно решить с составления пропорции:

х ч — 3/3пути (или весь путь — 1)

х= (1 *1 час) : 1/3 пути=1* 3/1=3

значит, весь путь поезд проедет за 3 часа.

1) в третий день ледокол проплыл 3/8. это составляет 90 км. тогда путь за последние два дня равен 90/3*8=240 км.

2) во второй день ледокол проплыл 240-90=150 км

3) за два последних дня ледокол проплыл 1-2/5=3/5 всего пути. и это составляет 240 км. тогда весь путь 240/3*5=400 км

4) в первый день ледокол проплыл 400-240=160 км.

ответ всего проплыл 400 км, в первый день 160 км, во второй день 150 км.

Источник

Динамическое программирование — базовые понятия

Общие принципы

Рассмотрим такую задачу: найти N-е число Фибоначчи.

Числа Фибоначчи определяются так: \(F_0 = 0, F_1 = 1, F_n = F_ + F_\) .

Эту задачу можно решить рекурсивно:

Однако это будет работать очень долго. 20-е число посчитать еще можно будет, а 40-е число — нет. И не потому, что числа большие. А потому, что мы будем делать слишком много лишней работы. Число операций будет экспоненциально относительно \(N\) .

Почему? Потому что, чтобы посчитать N-е число, нам нужно будет независимо посчитать (N-1)-е число и (N-2)-е число, и это в минимум в два раза больше действий, чем нужно для (N-2). А значит, для подсчета N-го числа Фибоначчи необходимо 2 раза посчитать (N-2)-е число, и это занимает в два раза больше времени, а значит это хотя бы \(2^\frac<2>\) действий.

Это ну слишком долго, и главное, что это легко исправляется. Давайте просто не считать лишних действий — если мы один раз посчитали \(F_k\) , то давайте запомним, чему оно равно, и в следующий раз, когда оно нам понадобится, мы используем его сразу. Удобнее всего сохранить числа Фибоначчи прямо в массиве:

И этот способ легко работает для больших \(N\) , так как работает за \(O(N)\) — всего один проход по массиву (правда здесь ответ мы будем считать по модулю \(10^9\) , потому что иначе числа получатся слишком слишком большими):

Это и называется динамическим программированием (или динамикой, ДП). Основная идея состоит в том, чтобы * свести задачу для \(N\) к задаче для чисел, меньших, чем \(N\) (с помощью формулы) * хранить все ответы в массиве * заполнить начало массива вручную (для которых формула не работает) * обойти массив и заполнить ответы по формуле * вывести ответ откуда-то из этого массива

Чтобы решить задачу по динамике вы должны ответить на 5 вопросов: * Что лежит в массиве? (самый важный вопрос чаще всего) * Как инициализировать начало массива? * Как обходить массив? (чаще всего слева направо, но не всегда) * Какой формулой считать элементы массива? * Где в массиве лежит ответ?

Одномерная динамика: кузнечик

Рассмотрим такую задачу:

Есть полоска \(1\times N\) , кузнечик стоит на первой клетке, он может прыгать вперед на 1, 2, 3 клетки. Сколько есть способов добраться от начальной клетки до последней?

Как решать такие задачи? Нужно придумать рекуррентную формулу, как ответ для N зависит от ответа для меньших чисел.

Очень помогает посмотреть на маленькие числа (!! одна из самых важных идей для придумывания решений):

Пусть dp[x] — это количество способов добраться от 1 клетки до клетки номер x.

• dp[1] = 1 способ (стоять на месте)
• dp[2] = 1 способ ( \(1 \rightarrow 2\) )
• dp[3] = 2 способа ( \(1 \rightarrow 2 \rightarrow 3\) и \(1 \rightarrow 3\) )
• dp[4] = 4 способа ( \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4\) и \(1 \rightarrow 3 \rightarrow 4\) и \(1 \rightarrow 2 \rightarrow 4\) и \(1 \rightarrow 4\) )
• dp[5] = 7 способов ( \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5\) и \(1 \rightarrow 3 \rightarrow 4 \rightarrow 5\) и \(1 \rightarrow 2 \rightarrow 4 \rightarrow 5\) и \(1 \rightarrow 4 \rightarrow 5\) и \(1 \rightarrow 2 \rightarrow 3 \rightarrow 5\) и \(1 \rightarrow 3 \rightarrow 5\) и \(1 \rightarrow 2 \rightarrow 5\) )

Дальше становится сложнее. Но можно заметить закономерность. А можно и не заметить, но зато если мы сейчас придумаем формулу, мы легко проверим, работает ли она. Заодно мы получили наши значения на маленьких числах, которые нам все равно понадобится вбить в программу.

Какой последний прыжок кузнечика в его пути до N-й клетки? Один из трех вариантов: * \((N — 1) \rightarrow N\) * \((N — 2) \rightarrow N\) * \((N — 3) \rightarrow N\)

То есть все пути до \(N\) разбиваются на 3 группы. Причем мы знаем сколько путей в каждой группе. В первой из них ровно dp[N — 1] путей — столько путей идут до (N-1)-й клетки, и дальше идет еще один прыжок. Во второй и третьей группах поэтому тоже dp[N — 2] и dp[N-3] путей.

Так что формула получается такой: dp[N] = dp[N — 3] + dp[N — 2] + dp[N — 1].

Очень похоже на числа Фибоначчи, да? Можете посмотреть на числа, которые мы уже выписали, там все отлично подходит:

dp[4] = 4 = 1 + 1 + 2 = dp[1] + dp[2] + dp[3]

dp[5] = 7 = 1 + 2 + 4 = dp[2] + dp[3] + dp[4].

Так что программа пишется легко:

Давайте изменим немного задачу: Теперь некоторые из клеток закрыты. То есть нам известно про конкретные клетки, что на них кузнечик прыгать не может. Тогда задача все еще решается так же, только нужно убедиться, что dp[x] = 0 для всех запрещенных x!

Также немного перепишем код, чтобы не писать отдельно случаи для 2 и 3, а также чтобы не писать в формуле сумму трех чисел (а представьте, что в задаче не 3, а 100). Будем инициализировать только dp[1]. А ко всем следующим значениям dp[i] будет прибавлять dp[i — k], где k = 1, 2, 3. Причем, если i — k \(0\times0\) до \(i\times j\) ” (заменим 1-нумерацию на 0-нумерацию). Будем хранить это в двумерном массиве dp в клетке dp[i][j].

Сразу понятны некоторые свойства этого массива: * Он размера NxM * dp[0][0] = COINS[0][0] * ответ на всю задачу лежит в dp[N — 1][M — 1]

Но гораздо важнее придумать формулу для подсчета dp[i][j] через предыдущие. Легко посчитать первую строку и первый столбец: * dp[0][k] = dp[0][k — 1] + COINS[0][k] * dp[k][0] = dp[k — 1][0] + COINS[k][0]

Так как до этих клеток есть ровно один путь.

Но что делать, если есть много путей до клетки dp[i][j]? Снова разобьем их на на несколько групп в зависимости от последнего хода (! важный трюк, запомните). Последний ход был: * либо из [i][j — 1] * либо из [i — 1][j]

Поэтому формула для максимального числа монет такая: dp[i][j] = max(dp[i — 1][j], dp[i][j — 1]) + COINS[i][j].

Ну все, достаточно пройтись правильно по двумерному массиву (построчно сверху вних, а в каждой строке слева направо) и заполнить этот массив.

В отличие от жадного алгоритма, динамическое программирование находит оптимальное решение — это, в данном случае, 113 монет.

Восстановление ответа

В последней задаче было здорово найти, что в оптимальном пути черепашки набирается 113 монет, но интересно, что именно это за путь. Такую задачу называют восстановлением ответа в динамике.

Есть два способа, которыми можно это сделать.

1. Хранить в массив prev откуда ты пришел в эту клетку.

Когда мы выбираем максимум из левой и верхней клетки, мы на самом деле решаем, какой последний ход будет в оптимальном пути до этой клетки — сверху или слева, и берем ответ для той клетки, сложнный с монетами в этой клетке. Давайте координаты клетки, откуда мы пришли, хранить в массиве prev. Или, в данном случае, можно хранить не координаты а просто 1, если пришли слева, и 0, если пришли сверху.

И, чтобы восстановить ответ, надо просто пройтись с конца по этим клеткам до самого начала, и развернуть получившуюся последовательность.

1. Вместо хранения массива prev догадаться по массиву dp, откуда именно черепашка пришла в эту клетку.

В данном примере это довольно легко. Если мы уже посчитали весь массив dp, то теперь можно начиная с конца легко понять, пришла черепашка туда сверху или слева в оптимальном маршруте — она пришла из клетки с максимальным числом монет.

Задание

Решите как можно больше задач из простого контеста:

А также решите как можно больше задач из сложного контеста:

Разбор еще нескольких задач

Давайте разберем еще несколько задач.

Последовательности без 3 единиц подряд

Условие:

Определите количество последовательностей из нулей и единиц длины \(N\) , в которых никакие три единицы не стоят рядом.

Решение:

Давайте хранить в \(dp[N]\) ровно число таких последовательностей длины \(N\) (это первое, что должно приходить в голову).

Давайте посмотрим для начала для маленьких чисел:

• \(dp[0] = 1 (\text<пустая последовательность>)\)
• \(dp[1] = 2 (0, 1)\)
• \(dp[2] = 4 (00, 01, 10, 11)\)
• \(dp[3] = 7 (000, 001, 010, 011, 100, 101, 110)\)
• \(dp[4] = 13 (0000, 0001, 0010, 0011, 0100, 0101, 0110, 1000, 1001, 1010, 1011, 1100, 1101)\)

Сходу закономерность можно не увидеть. Нужно догадаться сгруппировать эти числа по том, сколько в конце единичек. Например, для dp[4]:

• 0 единичек в конце: \(0000, 0010, 0100, 0110, 1000, 1010, 1100\) — их ровно семь, как для \(N=3\) , потому что первые 3 числа могут быть любые (но без трех единиц подряд), а четвертое — 0
• 1 единичка в конце: \(0001, 0101, 1001, 1101\) — их ровно четыре, как для \(N=2\) , потому что первые 2 числа могут быть любые (но без 3 единиц подряд), а два последних — 01
• 2 единички в конце: \(0011, 1011\) — их ровно две, как для \(N=1\) , потому что первое число может быть любым (но без 3 единиц подряд), а три последних — 011

Так мы замечаем и доказываем формулу: \(dp[N] = dp[N-1] + dp[N-2] + dp[N-3]\)

Теперь за \(O(N)\) ее легко посчитать.

Лесенки

Условие:

Лесенкой называется набор кубиков, в котором каждый горизонтальный слой содержит меньше кубиков, чем слой под ним. Подсчитать количество различных лесенок, которые могут быть построены из N кубиков.

Решение:

Если считать, что \(dp[N]\) — это число лесенок из \(N\) кубиков, то никакой закономерности скорее всего найти не получится.

• \(dp[1] = 1\)

■

• \(dp[2] = 1\)

■

■

• \(dp[3] = 2\)

■
■	■

■

■

■

• \(dp[4] = 2\)

■
■	■	■

■

■

■

■

• \(dp[5] = 3\)

■	■
■	■	■

■
■	■	■

■

■

■

■

■

• \(dp[6] = 4\)

■
■	■
■	■	■

■	■
■	■	■	■

■
■	■	■

■

■

■

■

■

■

По числам построить закономерность сложно, и по самим лесенкам тоже. Не видно какого-то рассуждения вида “ко всем лесенкам размера N-1 можно положить на любой слой еще один кубик”, иногда ведь и нельзя.

Тут нам помогает введение дополнительного параметра. Нас просят решить одномерную задачу (для \(N\) ), а мы решим двумерную задачу для \(n\) и \(m\) . Давайте зафиксируем размер самого нижнего слоя и назовем его размер \(m\) .

То есть $dp[n][m] = $“число лесенок, состоящих из \(N\) кубиков, таких, что самый нижний слой состоит из \(M\) кубиков”.

Как это связано с нашей задачей? Ответ на нашу задачу равен \(dp[N][1] + dp[N][2] + \ldots + dp[N][N]\) .

Какая есть формула для такой постановки задачи? Размер нижнего слоя у нас зафиксирован и равен \(m\) , осталость \(n-m\) кубиков на верхних слоях. Логично перебрать размер второго снизу слоя, который может быть любым от \(1\) до \(m-1\) : \(dp[n][m] = dp[n-m][1] + dp[n-m][2] + \ldots + dp[n-m][m-1]\)

Это все пир условии, что \(n \geq m\) . Иначе \(dp[n][m] = 0\) .

Теперь осталось понять как инициализировать этот массив и аккуратно по нему пройтись. Давайте инициализируем его ровно для случая \(n=0, m=0\) :

Пройдемся по массиву сначала для всех m при n = 1, потому для всех m при всех n = 2 и так далее — то есть по строчкам обычными двумя циклами \(for\) .

Для \(m > 0\) в ячейках \(dp[0][m]\) наш алгоритм будет работать и возвращать 0, так как \(n .

Для всех \(n > 0\) наша формула будет находить ответ через числа с меньшим n, а значит алгоритм корректен.

Он заполняет табличку размера \(N^2\) , обрабатывая каждую клетку за \(O(N)\) операций, итоговое время работы — \(O(N^3)\) .

Источник