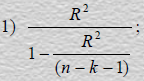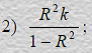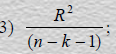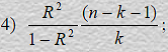Наилучший способ устранения автокорреляции установление ответственного за нее фактора

Наилучший способ устранения автокорреляции установление ответственного за нее фактора

181. Модель скользящего среднего СС (q) описывается соотношением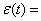
•

182. Модель СС (1) описывается соотношением
•

183. Модель СС (1) стационарна при:
• любых

184. Модель СС (2) описывается соотношением
•

185. Модель, заданная зависимостью у = 12 + + u, относится к модели:
• нелинейной по переменным

186. На больших временах __________________ факторы описываются монотонной функцией.
• долговременные

187. На больших временах процесс формирования значений временного ряда находится под воздействием __________________ факторов.
• долговременных и циклических

188. На первом этапе применения теста Голдфелда-Квандта в выборке все наблюдения
• Упорядочиваются по возрастанию х

189. На третьем шаге Зарембки рассматривается линейная регрессия с наблюдениями __________________ вместо исходных у_i:
• у_{i* = yi / геом}

190. На экзамене в группе из 15 студентов 4 человека получили отличную оценку, 8 человек — оценку хорошо, 3 человека — оценку удовлетворительно. Средний бал по группе равен:
• 4,06

191. Наблюдение зависимой переменной регрессии в предшествующий момент, используемое как объясняющая переменная, называется __________________ переменной.
• лаговой

192. Набор категорий представляет собой конечный набор __________________ событий.
• взаимоисключающих

193. Наиболее частая причина положительной автокорреляции заключается в постоянной направленности воздействия __________________ переменных.
• не включенных в уравнение

194. Наилучший способ устранения автокорреляции — установление ответственного за нее фактора и включение соответствующей __________________ переменной в регрессию.
• объясняющей

195. Невыполнение 2 и 3 условий Гаусса-Маркова, приводит к потере свойства __________________ оценок.
• эффективности

Источник

Итоговый тест по дисциплине «Эконометрика». Вариант №1. Тест 1

Поможем успешно пройти тест. Знакомы с особенностями сдачи тестов онлайн в Системах дистанционного обучения (СДО) более 50 ВУЗов. При необходимости проходим систему идентификации, прокторинга, а также можем подключиться к вашему компьютеру удаленно, если ваш вуз требует видеофиксацию во время тестирования.

Закажите решение за 470 рублей и тест онлайн будет сдан успешно.

1. При расчете t-статистики через коэффициент детерминации для оценки уравнения
множественной регрессии используется формула:

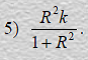
2. При использовании метода Монте-Карло результаты наблюдений генерируются с помощью:
1) анализа зависимостей
2) решения системы уравнений
3) опросов
4) датчика случайных чисел
5) тестов

3. Тест Фишера является:
1) двусторонним
2) односторонним
3) многосторонним
4) многокритериальным
5) трехшаговым

4. Выборочная корреляция является __________оценкой теоретической корреляции:
1) точной
2) состоятельной
3) эффективной
4) несмещенной
5) случайной

5. Если все наблюдения лежат на линии регрессии, то коэффициент детерминации R2 для
модели парной регрессии равен:
1) нулю
2) 2/3
3) единицы
4) ½
5) 0

6. Фиктивная переменная взаимодействия – это __________ фиктивных переменных:
1) произведение
2) среднее
3) разность
4) сумма
5) отношение

7. МНК автоматически дает ___________ для данной выборки значение коэффициента де-
терминации R2:
1) минимальное
2) максимальное
3) среднее
4) средневзвешенное
5) случайное

8. Для автокорреляции характерным является соотношение (u u ) __ 0: k i COV
1) >
2) 2
4) > 1
5) = 1

14. Линия регрессии _______ через точку ( , ) :
_ __
x y
1) может пройти
2) всегда проходит
3) несколько раз проходит
4) никогда не проходит
5) может пройти или не пройти

15. Из перечисленных факторов: 1) число объясняющих переменных, 2) количество наблюдений в выборке, 3)конкретные значения переменных, − критические значения статистики Дарбина-Уотсона зависят от:
1) 1, 2, 3
2) 3
3) 1, 2
4) 2
5) 3, 2

16. Определение отдельного вклада каждой из независимых переменных в объясненную
дисперсию в случае их коррелированности является ___________ задачей:
1) достаточно простой
2) невыполнимой
3) достаточно сложной
4) первостепенной
5) выполнимой

17. Зависимая переменная может быть представлена как фиктивная в случае если она:
1) подвержена сезонным колебаниям
2) имеет трендовую составляющую
3) является качественной по своему характеру
4) трудноизмерима
5) не подвержена сезонным колебаниям

18. Значение статистики DW находится между значениями:
1) -3 и 3
2) 0 и 6
3) -2 и 2
4) 0 и 4
5) -1 и 1

19. Наилучший способ устранения автокорреляции – установление ответственного за нее
фактора и включение соответствующей ___________ переменной в регрессию:
1) фиктивной
2) объясняющей
3) сезонной
4) зависимой
5) циклической

20. Значения t-статистики для фиктивных переменных незначимо отличается от:
1) 1
2) 0
3) -1
4) ½
5) 2

Источник

Автокоррелированность случайной компоненты, ее обнаружение и устранение, страница 2

Описание файла

Документ из архива «Автокоррелированность случайной компоненты, ее обнаружение и устранение», который расположен в категории «рефераты, доклады и презентации». Всё это находится в предмете «эконометрика» из шестого семестра, которые можно найти в файловом архиве РТУ МИРЭА. Не смотря на прямую связь этого архива с РТУ МИРЭА, его также можно найти и в других разделах. Архив можно найти в разделе «рефераты, доклады и презентации», в предмете «эконометрика» в общих файлах.

Онлайн просмотр документа «Автокоррелированность случайной компоненты, ее обнаружение и устранение»

Текст 2 страницы из документа «Автокоррелированность случайной компоненты, ее обнаружение и устранение»

Рисунок 4. тест Дарбина-Уосона на автокорреляцию (отрицательную)

Устранение автокорреляции

Наилучший, но не всегда возможный, способ устранения автокорреляции – установление ответственного за нее фактора и включение соответствующей объясняющей переменной в регрессию.

В других случаях процедура, которую следует принять для устранения автокорреляции, будет зависеть от ха­рактера зависимости между значениями случайного члена. В литературе наиболь­шее внимание уделяется авторегрессионной схеме первого по­рядка _, так как она интуитивно правдоподобна, но для того, чтобы было целесообразным ее использование в более сложных моделях, оснований обыч­но не хватает. Вместе с тем, если наблюдения проводятся ежеквартально или ежемесячно, могут оказаться более подходящими другие модели.

Если бы уравнение было правильной спецификацией для измерения величины случайного члена, то возможно было бы полностью устранить автокорре­ляцию, если бы знали величину ρ. Это будет продемонстрировано на примере уравнения регрессии, включающего только одну объясняющую переменную, од­нако при большем их числе действует тот же принцип.

Предположим, что истинная модель задается выражением:

,

так что наблюдения k и (k – 1) формируются как:

,

Теперь вычтем из обеих частей уравнения умноженное на ρ соотноше­ние и получим:

.

Обозначим , , и .

Тогда формулу мож­но переписать как

.

Вместе с тем из уравнения имеем . Таким образом, фор­мула принимает вид: .

Если ρ известно, тогда можно вычислить величины , , и (последняя одинакова для всех наблюдений) для наблюдений, включающих от 2 до n исходных данных. Если теперь оценить регрессию между , , и (за­метим, что в уравнение не должна включаться постоянная), то будут получены оценки α и β, не связанные с проблемой автокорреляции, поскольку, согласно предположению, значения е не зависят друг от друга.

Остается небольшая проблема. Если в выборке нет данных, пред­шествующих первому наблюдению, то невозможно вычислить , , и по­теряется первое наблюдение. Число степеней свободы уменьшается на единицу, и это вызовет потерю эффективности, которая может в небольших выборках пе­ревесить повышение эффективности от устранения автокорреляции.

Эту проблему можно довольно легко обойти, пользуясь так поправкой Прайса – Уинстена.

Поправка Прайса–Уинстена – метод спасения первого наблюдения в автокорреляционной схеме первого порядка.

Случайный член e, согласно определению, не зависит от значения и в любом предшествующем на­блюдении. В частности, все величины e₂,…,e_τ не зависят от u₁. Следовательно, если при устранении автокорреляции все другие наблюдения преобразуются, то не требуется преобразовывать первое наблюдение. Можно сохранить его, включив в новую схему, полагая, что , , .

Таким способом возможно спасти первое наблюдение, но здесь есть неболь­шая проблема, которую требуется решить. Если ρ велико, то первое наблюде­ние будет оказывать непропорционально большое воздействие на оценки, ис­численные по уравнению регрессии. Чтобы нейтрализовать этот эффект, умень­шим вес данного наблюдения умножением его на величину , полагая что , и .

Конечно, на практике величина р неизвестна, его оценка получается одновременно с оценками α и β. Имеется несколько стандартных способов такого оценивания, например, метод Кокрана — Оркатта.

Метод Кокрана–Оркатта – компьютерный итерационный метод устранения автокорреляции первого порядка.

Метод Кокрана–Оркатта с поправкой Прайса – Уинстена итерационно оценивает α, β₁, β₂, . β_m и коэффициент r в авторегрессионной схеме, пока разница между результатами итераций не станет очень малой. Реализуется только на компьютере.

Метод Кокрана – Оркатта включает следующие этапы.

Оценивается регрессия с исходными непреобразованными дан­ными.

Оценивается регрессионная зависимость е_k от е_k-1, соответствующая формуле _, и коэффициент при e_k+1, представляет собой оценку ρ.

С этой оценкой ρ уравнение преобразуется в , оценива­ние которого позволяет получить пересмотренные оценки α и β.

Повторно вычисляются остатки, и процесс возвращается к этапу.

Заключение

Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента корреляции ρ между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Данное понятие широко используется в эконометрике. Наличие автокорреляции случайных ошибок регрессионной модели приводит к ухудшению качества оценок параметров регрессии, а также к завышению тестовых статистик, по которым проверяется качество модели (то есть создается искусственное улучшение качества модели относительно её действительного уровня точности). Поэтому тестирование автокорреляции случайных ошибок является необходимой процедурой построения регрессионной модели.

Список литературы

Елисеева И.И. Эконометрика: Учебник. – М.: Экзамен, 2009.

Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник. – М.: Дрофа, 2008.

Луговская Л.В. Эконометрика в вопросах и ответах: Учебное пособие. – М.: Академия, 2009.

Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – М.: Дело, 2010.

Мардас А. Н. Эконометрика: Учебник. – М.: Финансы и статистика, 2009.

Орлов А.И. Эконометрика: Учебник. – М.: Феникс, 2009.

Толоконников Л. А., Кочетыгов А. А.Основы эконометрики: Учебное пособие. – М.: Феникс, 2009.

Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2010.

Эконометрика: учебник для бакалавров / под ред. И.И. Елисеевой. – М.: Проспект, 2013.

Источник