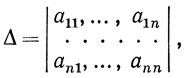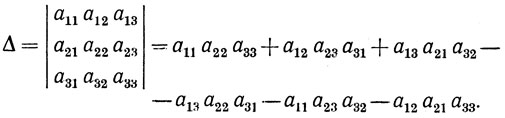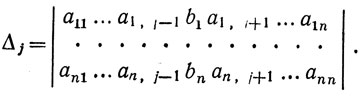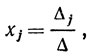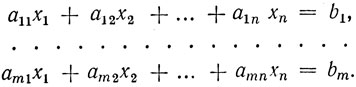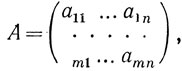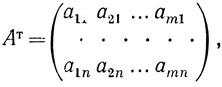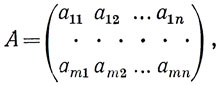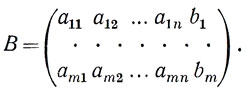Наиболее распространенный способ решения злп с двумя переменными это

Наиболее распространенный способ решения злп с двумя переменными это

§ 4. Методы решения задач линейного программирования

Существует довольно много методов решения задач линейного программирования. Мы коснемся наиболее распространенных из этих методов и по возможности покажем границы их применимости. В данном параграфе описываются простейшие методы, пригодные в основном для решения задач с небольшим числом переменных. Однако, несмотря на простоту и наглядность, эти методы содержат в себе элементы подхода к решению класса задач, значительно более сложных, выходящих за пределы предположений, используемых в линейном программировании.

1. Графический метод. Если было указано, что в тех случаях, когда множество планов задачи линейного программирования образует выпуклый многогранник, линейная функция цели достигает своего оптимального значения в одной из вершин этого многогранника. Это свойство множества планов будет использовано для решения задачи линейного программирования.

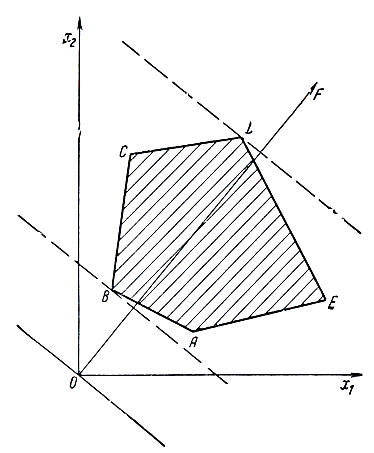
Начнем с простого примера, представленного графически на рис. 1.2. Предположим, что в пространстве двух измерений (x₁, x₂) даны выпуклый многоугольник ABCDE, внутренняя область которого является множеством планов задачи, и линейная функция пели f = c₁x₁ + c₂x₂, где c₁>0, c₂>0. Пусть сначала f = 0. При этом прямая c₁x₁ + c₂x₂ = 0 проходит через начало координат. В данном случае точка x₁ = 0, x₂ = 0 не принадлежит многоугольнику решений. Для того чтобы функция f стала соответствовать допустимым решениям задачи, необходимо добиться пересечения прямой f = c₁x₁ + c₂x₂ = const с многоугольником ABCDE. Будем придавать f все увеличивающиеся положительные значения. При этом прямая будет передвигаться вправо, оставаясь параллельной самой себе.

Рис. 1.2

Действительно, можно записать уравнение прямой в виде x₂ = — c₁ /_c2x₁ + f /_c2. Из аналитической геометрии известно, что величина — c₁ /_c2 определяет угол наклона этой прямой к осям координат. При изменении f этот угол не меняется и прямая передвигается параллельно самой себе в направлении перпендикуляра OF.

Перемещая таким образом прямую f = c₁x₁ + c₂x₂ = const, мы впервые встречаем многоугольник ARCDE в вершине В, где эта прямая становится опорной прямой. Поскольку вершина В находится ближе всего к точке О, она имеет наименьшие координаты (x₁, x₂) и, следовательно, функция f достигает в вершине В наименьшего значения. Перемещая прямую далее, мы, наконец, приходим в вершину D, которая является наиболее удаленной от начала координат точкой многоугольника ABCDE. В этой вершине, очевидно, функция цели f достигает наибольшего значения.

Иногда может случиться, что прямая f = c₁x₁ + c₂x₂ = 0 окажется параллельной одной из сторон выпуклого многоугольника. Тогда линейная функция f = c₁x₁ + c₂x₂ достигает своего наименьшего или наибольшего значения в любой точке, принадлежащей этой стороне. Но и в этом случае функция f достигает этих значений в вершинах, лежащих на этой стороне.

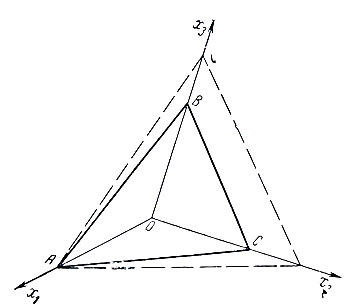
Имеется полная аналогия вышеизложенному при решении задач в пространстве трех измерений. Если заданы многогранник решений в пространстве трех измерение АВСО (рис. 1.3) и линейная функция цели f = c₁x₁ + c₂x₂ + c₃x₃, то проводя плоскость c₁x₁ + c₂x₂ + c₃x₃ = 0 через начало координат и передвигая ее параллельно самой себе (в направлении перпендикуляра, восстановленного к этой плоскости) до встречи с ближайшей к началу координат вершиной многогранника, находим минимальное значение функции цели (на рис. 1.3 вершина О уже дает минимум f). Наиболее удаленная от начала координат вершина A, очевидно, определяет наибольшее значение функции f. На рис. 1.3 пунктиром обозначены линии обозначены линии пересечения плоскости f = const с плоскостями (x₁, x₂), (x₁, x₃), (x₂, x₃).

Рис. 1.3

Напомним, что при решении экономических задач интересуются в основном неотрицательными решениями, т. е. из всех возможных решений считаются допустимыми лишь решения x₁≥0, x₂≥0, . x_n≥0. Очевидно, что все решения задачи, иллюстрированной рис. 1.2, удовлетворяют этому требованию, поскольку многоугольник ABCDE целиком расположен в первом квадранте системы координат (x₁, x₂). В этом случае требования x₁≥0, x₂≥0 удовлетворяются автоматически и фактически не являются ограничениями. Однако для примера (рис. 1.3) требования x₁≥0, x₂≥0, x₃≥0 явным образом входят в формулировку задачи, являясь ограничениями, определяющими положение трех из четырех граней многогранника. Поэтому об ограничениях вида x_i≥0 всегда следует помнить при решении экономических задач линейного программирования.

Для задач, заданных в пространстве трех измерений, на плоском чертеже зачастую трудно графически отобразить положение многогранника решений и представить взаимное положение этого многогранника и плоскости, определяющей целевую функцию. Поэтому графическое решение тих задач часто оказывается затруднительным.

Графическое решение задач в случае n переменных для n>3 практически не может быть получено, учитывая то обстоятельство, что n-мерное пространство (n>3) является абстрактным математическим понятием.

Таким образом, можно считать, что графический метод , решения задач линейного программирования пригоден в основном для решения задач, заданных в пространстве двух или трех измерений.

2. Алгебраические методы. Поскольку с самого начала основная задача линейного программирования была сформулирована в виде системы m линейных уравнений с n неизвестными, то естественно обратить основное внимание на алгебраические методы решения задачи. При этом описанная выше в § 3 геометрическая интерпретация будет являться фактором, обеспечивающим ориентацию в направлении наиболее быстрого получения решения.

Предварительно кратко, без доказательств, напомним некоторые сведения из линейной алгебры.

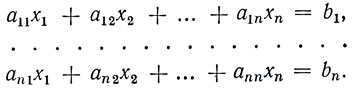
Рассмотрим систему n линейных уравнений с n неизвестными:

Величина, составленная из коэффициентов a₁₁, . a_nn этой системы и записанная следующим образом:

называется определителем системы n-го порядка. Такая формальная запись подразумевает существование некоторого правила для вычисления Δ. Согласно этому правилу определитель n-го порядка представляет из себя алгебраическую сумму n! = 1*2*3*. *n слагаемых вида a_1,i1*a_2,i2. a_n,in, состоящих из n сомножителей, взятых по одному из каждой строки и каждого столбца. В том случае, если слагаемые, у которых вторые индексы сомножителей i₁, i₂, . i_n образуют так называемую четную перестановку, берется знак (+), если перестановка нечетная, то знак (-).

Перестановка из n чисел (индексов) называется четной, если число нарушений принятого порядка следования чисел в ней (число инверсий) четно, и нечетной, если число этих нарушений нечетно. Например, числа 1, 2, 3, 4, 5, записанные в принятом порядке возрастания, образуют перестановку. Меняя порядок расположения этих цифр, получим другие перестановки: (1, 3, 2, 4, 5), (1, 2, 4, 3, 5) и т. д. Всего может быть 5! = 120 перестановок из пяти элементов. Из n различных элементов можно составить n! перестановок. Нарушение принятого порядка следования чисел, таким образом, имеется у всех, кроме одной, перестановок.

Сформулированное выше правило вычисления определителя я-го порядка можно записать в виде

где t — число инверсий в перестановке (i₁, i₂, . i_n).

В качестве примера выпишем определитель третьего порядка, состоящий из 3! = 6 чисел:

Можно легко проверить справедливость общей формулы на примере этого определителя. Вычисление определителей более высокого порядка также не представляет трудностей, хотя объем вычислений при этом сильно возрастает.

Если теперь в определителе системы Δ заменить j-й столбец столбцом свободных членов, то получим определитель

В том случае, если определитель системы Δ≠0, система из n уравнений с n неизвестными имеет единственное решение, определяемое равенствами

В том случае, если Δ = 0, система является либо несовместной, либо имеет бесконечное множество решений.

Перейдем теперь к наиболее общему случаю системы m линейных уравнений с n неизвестными (система вида (1.1)):

Прямоугольная таблица, составленная из коэффициентов этой системы

называется матрицей системы. Матрица в частном случае может состоять из одной строки (матрица-строка) или из одного столбца (матрица-столбец).

Если в матрице А переставить строки со столбцами, то получим новую матрицу

которая называется транспонированной матрицей по отношению к A. Соответственно и матрица А является транспонированной по отношению к A т .

Пусть для определенности в матрице Am≤. Из элементов этой матрицы, сохраняя порядок, в котором расположены ее элементы, можно образовать определители второго, третьего и т. д. до m-го порядков. Может случиться, что определители m-го, (m-1)-го и т. д. до (r+1)-го порядков включительно равны нулю, но хотя бы один определитель r-го порядка отличен от нуля. Тогда число r называется рангом матрицы А. Понятие ранга матрицы является весьма важным для линейного программирования. Укажем элементарные преобразования матриц, которые не меняют ее ранга:

1. вычеркивание из матрицы строки или столбца, состоящих из одних нулей;
2. умножение элементов строки или столбца на любое число (кроме нуля);
3. перестановка двух строк (или столбцов);
4. сложение элементов одной строки (или столбца) и соответствующих элементов другой строки (или столбца), умноженных на одно и то же число.

Матрица А и транспонированная к ней матрица А Т имеют один и тот же ранг.

Рассмотрим теперь две матрицы: одну, составленную из коэффициентов записанной выше системы уравнений

и другую, в которую введен столбец свободных членов этой системы

Матрица В называется расширенной по отношению к матрице А.

Источник

Решение задач линейного программирования

Решение происходит в три этапа:

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min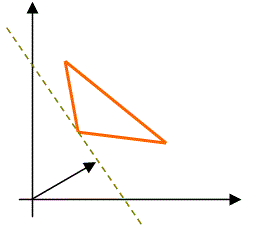

F(x) → max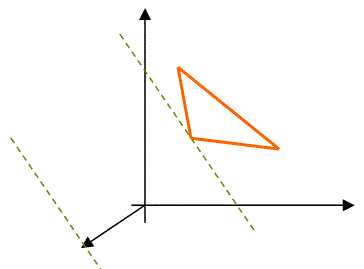

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Источник