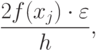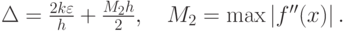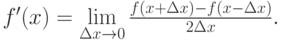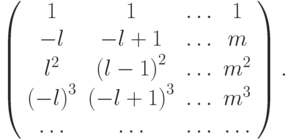Нахождение производной способом 4 шагов

Предмет вычислительной математики. Обусловленность задачи, устойчивость алгоритма, погрешности вычислений. Задача численного дифференцирования

1.6. Задача численного дифференцирования

В пункте «1.2» уже была введена простейшая формула численного дифференцирования . Рассмотрим задачу приближенного вычисления значения производной подробнее.

Пусть задана таблица значений x_i . В дальнейшем совокупность точек на отрезке, на котором проводятся вычисления, иногда будут называться сеткой, каждое значение x_i — узлом сетки. Пусть сетка — равномерная, и расстояние между узлами равно h — шагу сетки. Пусть узлы сетки пронумерованы в порядке возрастания, т.е.

Пусть f(x_j) = f_j — функция, определенная в узлах сетки. Такие функции будут называться табличными, или сеточными функциями. Считаем, кроме того, что рассматриваемая сеточная функция есть проекция (или ограничение) на сетку некоторой гладкой нужное число раз непрерывно дифференцируемой функции f(x) . По определению производной

тогда, если шаг сетки достаточно мал, по аналогии можно написать формулу в конечных разностях, дающую приближенное значение производной сеточной функции:

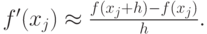( 1.1)

Если параметр h достаточно мал, то можно считать полученное значение производной достаточно точным. Погрешность формулы (1.1) оценена в пункте «1.2» . Как показано выше, при уменьшении шага сетки h ошибка будет уменьшаться, но при некотором значении h ошибка может возрасти до бесконечности. При оценке погрешности метода обычно считается, что все вычисления были точными. Но существует ошибка округления. При оценке ее большую роль играет машинный — мера относительной погрешности машинного округления, возникающей из-за конечной разрядности мантиссы при работе с числами в формате с плавающей точкой. Напомним, что по определению машинным называют наибольшее из чисел, для которых в рамках используемой системы вычислений выполнено Тогда абсолютная погрешность при вычислении значения функции (или представлении табличной функции) есть Максимальный вклад погрешностей округления при вычислении производной по формуле (1.1) будет

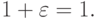
Пусть k = max |f(x)| , максимум ищется на отрезке, на котором вычисляются значения производных. Тогда суммарная ошибка, состоящая из погрешности метода и погрешности округления, есть

Для вычисления оптимального шага численного дифференцирования найдем минимум суммарной ошибки, как функции шага сетки

Если требуется повысить точность вычисления производных, необходимо воспользоваться формулами, имеющими меньшие погрешности метода. Так, из курсов математического анализа известно, что

По аналогии напишем конечно-разностную формулу

( 1.2)

(1.2) — формула с центральной разностью. Исследуем ее на аппроксимацию, т.е. оценим погрешность метода. Предположим, что функция, которую спроектировали на сетку, трижды непрерывно дифференцируема, тогда

Погрешность метода определяется 3-й производной функции. Введем , тогда суммарная погрешность при вычислении по формуле с центральной разностью есть

для вычисления оптимального шага, находя минимум погрешности, как функции шага сетки, имеем

Для более точного вычисления производной необходимо использовать разложение более высокого порядка, шаг h_opt будет увеличиваться.

Формула (1.1) — двухточечная, (1.2) — трехточечная: при вычислении производной используются точки (узлы) x_j (узел входит с нулевым коэффициентом), x_j + h, x_j — h — совокупность узлов, участвующих в каждом вычислении производной, в дальнейшем будем иногда называть сеточным шаблоном.

Введем на рассматриваемом отрезке шаблон из нескольких точек.

Считаем, что сетка равномерная — шаг сетки постоянный, расстояния между любыми двумя соседними узлами равны. Используем для вычисления значения первой производной следующую приближенную (конечно-разностную) формулу:

( 1.3)

шаблон включает l точек слева от рассматриваемой точки x_j и m справа. Коэффициенты — неопределенные коэффициенты. Формула дифференцирования может быть и односторонней — либо l , либо m могут равняться нулю. В первом случае иногда называют (на наш взгляд, не слишком удачно) такую приближенную формулу формулой дифференцирования вперед, во втором — формулой дифференцирования назад. Потребуем, чтобы (1.3) приближала первую производную с точностью O(h l + m ) . Используем разложения в ряд Тейлора в окрестности точки x_j . Подставляя их в (1.3), получим

Потребуем выполнение условий:

( 1.4)

Получаем систему линейных алгебраических уравнений для неопределенных коэффициентов (1.4). Матрица этой системы есть

Вектор правых частей (0, 1, 0, . 0) T .

Определитель данной матрицы — детерминант Вандермонда. Из курса линейной алгебры следует, что он не равен нулю. Тогда существует единственный набор коэффициентов , который позволяет найти на шаблоне из (1 + l + m) точек значение первой производной с точностью O(h l + m ) .

Для нахождения второй производной можно использовать ту же самую формулу (1.3) с небольшой модификацией

Очевидно, что и данная система уравнений для нахождения неопределенных коэффициентов имеет единственное решение. Для получения с той же точностью приближенных значений производных до порядка l + m включительно с точностью O(h l + m ) модификации формулы (1.3) и условий (1.4) очевидны, набор неопределенных коэффициентов находится единственным образом.

Таким образом, доказано следующее утверждение. На сеточном шаблоне, включающем в себя N + 1 точку, с помощью метода неопределенных коэффициентов всегда можно построить единственную формулу для вычисления производной от первого до n порядка включительно с точностью O(h N ) .

Утверждение доказано для равномерной сетки, но на случай произвольных расстояний между сеточными узлами обобщение проводится легко.

Так как на практике вычисления проводятся с конечной длиной мантиссы, то получить нулевую ошибку невозможно.

Читателям предлагается оценить значение оптимального шага при вычислениях по формулам типа (1.3) самостоятельно.

Источник

Решение производной для чайников: определение, как найти, примеры решений

• 4 июня 2021 г.
• 9 минут
• 599 972
• 15

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник