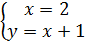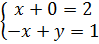Набор математических выражений указывающих способ получения решения задачи

Модель описания. Модель решения. Алгоритмическая модель. Программная модель

Эти модели представляют собой различные способы описания одних и тех же свойств объекта на разных фазах процесса моделирования от постановки задачи (словесного описания) до получения итоговых результатов.

Словесное описание объекта не является моделью, а является исходными данными (или представлением объекта) к рассмотрению.

Постановка задачи (словесное описание свойств объекта).

Модель описания – это предположение на математическом языке словесного описания (или описание в виде математических символов свойств объекта, изложенных в словесном описании).

Маша собрала 2 кг грибов, Саша на 1 кг больше. Сколько они собрали вместе?

X = 2 — это аналитическое описание

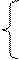
Модель решения – это набор зависимостей и правил в виде математических выражений, указывающих способ получения решения задачи.

· Аналитическая модель решения – представление искомой величины в виде явной зависимости через исходные данные.

(Для рассмотренной выше задачи) . Аналитическая модель решения будет иметь вид

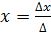
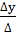
Решение системы линейных уравнений определяют по методу определителей (или его еще называют метод Крамера): , y = ,

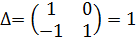
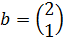
где – определитель системы линейных уравнений;

— вектор свободных членов.

Тогда

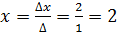
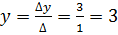
Решением является x=2, y=3

Численная модель решения – это набор выражений позволяющих получить решение в виде совокупности чисел. Решение в этом случае получаем приближенное. Данная модель применяется, если аналитическая модель очень сложна или ее просто не существует. (В качестве примера использование метода Ньютона для решений уравнения вида f(x)=0)

пусть f(x)=x 2 +x-s=0, выбор точки нач. приближения x₀=0,5 ; затем вычисление более точного решения по рекуррентной формуле.

Имитационная модель решения – предположение на язык ПК формальных правил, по которым функционирует объект моделирования согласно словесному описанию или аналитической модели описания. Эти правила позволяют при заданных входах определить выходные параметры. Данная модель используется для решения очень сложных задач, для которых как правило не важно составить алгоритмическую модель описания, а существует лишь словесное описание.

Алгоритмическая модель – запись модели решения в виде алгоритма (блок-схемы).

Теоретическая модель получено как логическое следствие некоторых фундаментальных законов природы или из некоторых других результатов исследования, возведенных в ранг истории.

Экспериментальная модель получена с помощью математической обработки результатов.

Пример. Получим уравнение (модель) равноускоренного движения двумя способами

· Теоретический способ. В качестве отправной точки (исходных данных) возьмем два закона (два определения)

1) Определение ускорения — ускорение это вторая производная координата по времени (ФОРМУЛА)

2) Движение называют равноускоренным, если его ускорение равно (ФОРМУЛА

· Эмпирический способ. Предположим, провели ряд экспериментов, пуская тяжелые шары по наклонным желобам. Меняем угол наклона желоба, что бы уменьшилось ускорение а. Меняем длину желоба, что бы изменялся путь х. Фиксируем время t в каждом эксперименте. Получим таблицу значений :

t	a	X
0,15
13,5
12,5

Отметим отличия теоретической и экспериментальной моделей

Фактор	Теоретическая модель	Экспериментальная модель
1.Способ получения	Логическое следствие законов природы	Математическая обработка экспериментов
2. Сложность исследований объекта	Сложные и всесторонние исследования	Относительно простая серия экспериментов
3. Сложность структуры модели	Высокая сложность: системы дифференциальных и алгоритмических уравнений, которые нужно решать (т.е. модель описания)	Невысокая сложность: явная зависимость выхода от входа (т.е. модель решения)
4. Область представления	Область широкая: могут быть включены даже точки, недоступные непосредственному наблюдению	Область узкая: вблизи экспериментальных точек

Замечание 1. При синтезе теоретической модели часто прибегают к упрощающим допущениям: некоторым предложением о свойствах объекта, при выполнении которых модель существенно упрощается.

Например, при равноускоренном движении мы пренебрегаем силой трения.

Наиболее типичные следующие упрощения:

1) полагаем какой — либо параметр = 0

2) полагаем какой — либо параметр =

3) полагаем, что два параметра линейно зависят друг от друга

Замечание 2. При теоретическом моделировании так же применяются эксперименты. Однако их роль существенно уже, чем в эмпирических моделях. Главным образом их используют для определения значений каких — либо параметров модели.

Например, при теоретическом выводе модель свободного падения имеет вид ФОРМУЛА

Критерии качества математической модели

Любому объекту можно построить множество моделей. Выбрать нужно ту, которая отвечает следующим критериям:

1) Универсальность – полнота описания свойств объекта

Пример. Имеем 10 моделей, каждая из которых описывает концентрацию парового вещества в жидкой фазе при различных движениях (ФОРМУЛА)

2) Точность – соответствие выходных параметров объекта, вычисленных по модели, их истинному (например, полученных из экспериментов). Точность бывает абсолютная и относительная. Чем меньше погрешность, тем больше точность.

3) Адекватность – способность модели правильно отображать свойства объекта. Это качественный показатель.

4) Экономичность – показатель суммарных затрат на получение и использование модели (затраты на оплату специалистов, затраты машинного времени и т.д.)

Источник

Набор математических формул и уравнений

Без этого, не совсем простого, умения, нельзя обойтись ни в одной науке. Естественно, что для математики, физики, химии, формулы и уравнения играют ключевую роль, но при проведении абсолютного большинства исследований потребуется показать расчетную формулу и/или пример расчетов.

Также велика потребность математического набора при оформлении многих реферативных работ учащимися от начальной школы до вуза.

Приведенный здесь текст намеренно не содержит некоторых вопросов, обсуждаемых на занятиях. Кроме того, он немного не завершен!

Для набора математических уравнений могут использоваться многочисленные программы, но мы остановимся на двух, наиболее востребованных и доступных вариантах: наборе простых формул в текстовом редакторе (на примере MS Word) и программе Equation Editor.

Внимание! На данный момент материал по работе с программами начинает переезд в создаваемый новый раздел.

Первичной задачей при наборе математических выражений следует считать принятие решения о среде набора. Причем не на глобальном уровне (что очевидно), а при вводе буквально каждого символа. К сожалению, мне неоднократно приходилось сталкиваться с ситуацией, когда автор научной статьи решает набирать переменные в тексте с использованием Microsoft Equation, даже если это одна буква. В результате выяснялось, что они просто не знали, что в текстовом редакторе можно применить к символам курсивное начертание. Чуть более сложных вариантов, также прекрасно набираемых в тексте, можно встретить неисчислимое множество.

Итак, математическое выражение можно набрать:

1. в примитивном текстовом редакторе;
2. в текстовом процессоре;
3. в специальной программе для набора математических формул;
4. в специальной программе для набора математических текстов.

В список намеренно не включена вставка формул, присутствующая в современных версиях Word. Обусловлено это тем, что мы, в первую очередь, рассматриваем набор для последующей публикации. Названный же вариант в настоящее время полностью несовместим с большинством издательских приложений, да и всеми остальными текстовыми процессорами тоже. Тупик.

В данном разделе обсуждается набор в тексте и общие правила размещения формул (они будут перенесены). Особенности работы с математическими программами см. здесь.

Способы ввода математики «в строку»

Первичная важность такого способа определяется, в первую очередь, использованием в программировании и в работе специализированных математических и статистических приложений.

Знаки математических действий (операторов), указание которых является обязательным:

плюс (+) — единственный непротиворечивый знак, имеющийся в двух местах: в цифровом ряду вместе с клавишей «=» и на дополнительной цифровой клавиатуре;

для обозначения минуса используется только дефис (-), присутствующий на стандартной клавиатуре в двух местах: в цифровом ряду за клавишей «0» и на дополнительной цифровой клавиатуре;

для обозначения умножения используется звездочка (*), также присутствующая дважды: в цифровом ряду (8) и на дополнительной цифровой клавиатуре;

деление указывается косой чертой (/, slash). Распространенной ошибкой является использование обратного знака (\, backslash), имеющего абсолютно другой смысл. Размещение клавиши не является абсолютно стандартизованным, но обычно она есть дважды: вместе с русскими точкой и запятой, а также на дополнительной цифровой клавиатуре;

возведение в степень обозначается символом крышки (^), проставляемого между основанием и показателем степени (клавиша «6»). Есть много ситуаций, когда этот стандартизованный вариант не работает в качестве программного;

наконец, существует так называемая экспоненциальная форма записи чисел, когда буква E используется для разделения мантиссы числа и его степени (для отрицательной — со знаком минуса) с основанием 10.
Пример: 6,02214076E23 = 6,02214129*10 23 (число Авогадро).

Дополнительная цифровая клавиатура должна быть стандартной, что значительно увеличивает скорость работы с ней.

В некоторых случаях проставление пробелов вокруг знаков математических действий является обязательным, в других — запрещено.

Следующим уровнем обработки выражения будет использование скобок для группировки действий. Данный способ работает всегда и везде, если используются только круглые скобки. Фигурные, квадратные и все остальные чаще всего запрещены либо имеют специальное назначение. При наборе текста «для себя», естественно, никаких ограничений нет.

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

В принципе, на этом все. Некоторые среды (электронные таблицы, языки программирования и т.д.) поддерживают множество дополнительных функций с определенным синтаксисом использования.

Набор в текстовом редакторе

В данном способе кроется только одно затруднение: не перегнуть палку с ограничением перехода в специализированную программу.

Начнем с истории. Всего лишь несколько десятилетий назад возможность форматированного ввода была присуща только особо развитым текстовым редакторам, а термин «процессор» в их отношении не использовался в принципе. Однако, запись математических выражений требовалась повсеместно.

С другой стороны, если хорошо подумать, то окажется, что сегодня все делается точно также.

Единственная сфера, претерпевшая значительные изменения силами программистов — веб-интерфейсы для пользователей, где теперь можно оформить текст почти как угодно сложно (в пределах возможностей HTML). Пусть и несколько с большими усилиями и только там, где поработала команда с интеллектом. Например, на данный момент, в веб-интерфейсе mail.ru, Яндекс-почты и Gmail невозможно ввести индексы. Но в последнем случае можно вставить их из буфера.

Ввод в текстовом процессоре

Поскольку в данном контексте рассматривается в первую очередь массовый ввод, на данный способ ложится абсолютно бóльшая часть работы. Это связано с определенной примитивностью вводимой информации, реализация особенностей которой тесно интегрирована в современных версиях программ. Хотя массовый переход на такую функциональность произошел около 30 лет назад.

Поскольку мы говорим о систематическом вводе математической информации, без знания горячих клавиш (клавиатурных сочетаний ускоренного доступа) набор становится чрезвычайно трудоемким. Так как перечень невелик, рекомендуется их полное заучивание.

Несколько более сложным действием является ввод спецсимволов, реализуемый несколькими способами. Знание их всех и использование в соответствии с текущей задачей — наиболее эффективный подход. Для знаков, встречающихся нечасто, но систематически, запоминание которых нецелесообразно, хочется порекомендовать составление заметок о предпочитаемом способе ввода.

Отметим, что квадратный корень, относящийся к единичному знаку (цифре или переменной), допускается указывать специальным символом (√).

Горячие клавиши в Word для набора формул и уравнений

Все перечисленные клавиши (клавиатурные сочетания, hot cut keys, keyboard shortcuts) нужны и их надо знать!

Клавиша	Действие	Комментарий
Начертания
Ctrl+I	Курсив (Italic)	Переменные. Самое частое использование!
Ctrl+B	Полужирное (Bold)	Векторные и матричные величины
Индексы
Ctrl+«+»	Нижний индекс (подындекс)	Число атомов, пояснения к переменной, основания
Ctrl+Shift+«+»	Верхний индекс (надындекс)	Степени чисел, заряды
Системные
Ctrl+«пробел»	Сброс (обнуление) всех характеристик символа, отличаюшихся от описанного в стиле	Крайне удобная клавиша, так как является универсальным выключателем и позволяет сбросить сразу несколько характеристик, присвоенных символам
Shift+«Enter»	Принудительное начало новой строки	Потребуется для контролируемого переноса уравнений
Символы
Ctrl+NumPad «-»	Минус
Shift+Ctrl+«пробел»	Неразрывный пробел
Shift+Ctrl+Q	Ввод одной греческой буквы	Необходимо знание соответствия

Специальные символы, вкратце, набираются следующим образом.

Для этого нужно набрать на дополнительной цифровой клавиатуре четырехзначный код символа при удерживаемой клавише Alt (Num Lock должен быть включен!).

Вводить часто встречающиеся символы можно с помощью их скан-кодов. Данный способ работает в любой программе! Примеры наиболее часто употребляемых знаков (в порядке возрастания кода):

• Alt+0137 (‰ — промилле)
• Alt+0149 (•, бюлетка, крупный знак умножения)
• Alt+0150 (–, минус)
• Alt+0176 (°, градус)
• Alt+0177 (±)
• Alt+0183 (⋅, маленький знак умножения)

Вместе с тем, для набора специальных символов можно воспользоваться командой меню Word: Вставка→Символ (Insert→Symbol). Искать бóльшую часть значков следует в шрифтах: основном (как в 8-битовом, так и Unicode), Symbol, MT Extra.

Обязательный набор в текстовом редакторе

То есть то, что не должно выносится в математическое приложение ни при каких обстоятельствах.

• Любые математические выражения без использования: верхних или нижних индексов; их сочетания одновременно (в одном месте); символики над и под знаками. Туда же следует отнести все случаи верхнего либо нижнего индекса, где все символы находятся на одном уровне. Всё — вне зависимости от набора используемых знаков.
• Надо четко понимать, что не существует ни одного текстового знака, отсутствующего для набора в тексте. Максимум — их может не содержать конкретный шрифт.

Примеры:
• переменные (x, N, n_мол.);
• Векторная/матричная величина (A);
• выражения;@
• уравнения.@

Рубеж перехода в специальное приложение

Этому уже посвящено немало оговорок и не следует забывать об условности проведения такой границы. Все, перечисляемое далее, следует рассматривать, разделив на две категории по назначению: для своих нужд или для последующей обработки другими людьми. В первом случае можно подобрать решение, удобное лично вам. Во втором — необходимо получение инструктивных указаний.

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Критерии выбора способа набора

Выбрать способ набора совсем несложно, но нередко принимается неверное решение. В его основе чаще всего лежит игнорирование возможных проблем. В чем они могут заключаться?

• Упрощенная для набора в тексте формула может совсем не восприниматься зрительно. Исполнитель забыл, что «понятность» — всегда наиважнейший критерий.
• Воспользоваться средствами поиска текстового редактора для обнаружения конкретного фрагмента в формуле уже не удастся. Программа только поможет последовательно найти все уравнения (то есть картинки).
• При желании перевести текст, содержащий формулы, в более простой формат (txt, HTML и т.п.), от формул не останется и следа.
• Исправить формулы можно только на компьютере, где установлен Equation Editor. А его версия должна быть не ниже той, в которой осуществлялся набор. Надо не забывать, что для правки потребуются навыки работы с программой.
• Шрифт (да и кегль), используемый в текстовом и формульном редакторах, могут не совпадать, и, вообще, оказаться несовместимым.
• Ввод арифметических знаков в формульном редакторе производится из шрифта Symbol, в связи с чем они отличаются (возможно, что весьма значительно) от обычного текста.

Некоторые причины ошибочного выбора способа набора.

• Незнание размещения клавиш на клавиатуре (верхнего ряда алфавитно-цифровой части).
• Незнание горячих клавиш текстового редактора (индексы, курсив, греческие буквы, спец. знаки, сброс оформления).
• Мнение, что за счет набора «картинкой» можно избежать нежелательных переносов.

Уравнение не развалится на разные страницы. Но и средства текстового редактора позволят это сделать, существенно повысив контроль над ситуацией.

Лень. Формульный редактор автоматически курсивит переменные и отбивает пробелами арифметические знаки.

Нумерация уравнений в текстовом документе

Применение нумерации определяется единственным фактором — необходимостью ссылки на него из текста, не прилегающего непосредственно к уравнению. Косвенно из этого вытекает, что не нужно уперто нумеровать все подряд, особенно если потребовалось отослать читателя к единственному уравнению.

Номер оформляется по требованиям конкретного издателя. В обобщенном виде можно говорить о следующих закономерностях.

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Ссылки на уравнения из текста подчиняются тем же требованиям, как и любой другой иллюстративный материал.@@@

Техническая реализация номера раньше не вызывала затруднений при наличии базовых знаний и устном пояснении. Так как ситуация изменилась, обсудим необходимые действия, по существу сводящиеся к созданию стиля.

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Общий смысл результата всех описанных действий отображен на рисунке.

Несложно заметить, что знаки равенства не расположены четко друг под другом и требуют дополнительной корректировки. Величину отступа прогнозировать бессмысленно, так как непредсказуем размер левой части уравнения.

И повторно акцентирую внимание на том, что даже для реализации данного примера произведена настройка стиля «Eq», уже присутствующего на компьютере. При оформлении других примеров будет соблюдено единство, что важно в том числе и при подготовке описания.

Дополнением для российского варианта будет связано с требованием выравнивать само уравнение по центру.

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Переносы формул

Первым и важнейшим правилом (№1) является нежелательность разбиения любого математического выражения на две или более строк. Но такая потребность нередка и может возникнуть в двух ситуациях: внутри текстового абзаца и в уравнениях, вынесенных в разрез полосы.

Приоритетность разрывов при переносе формул

Очень важно, что абсолютного описания сделать нельзя. Главным критерием должно быть удобство восприятия математической сущности читателем. Больше ничего.

Выравнивание формул в разрез полосы

Российские требования

Я отношу себя к категорическим противником требований, принятым у нас в стране. Считаю их одной из вершин тупости и необразованности. Описать обязан, но без энтузиазма.

Международные требования

В связи с тем, что отсутствует организация, которая взяла бы на себя эту тягостную обязанность, можно говорить лишь об обобщении практики ведущих научных издателей в области математики и физики.

1. Принципиальным является выравнивание всех уравнений по левому краю. Стандартным является отступ слева на размер красной строки.

Типовые ошибки при наборе формул

Доступ к этим материалам предоставляется только зарегистри­рован­ным пользователям!

Шрифты

Установка на компьютер программы Equation Editor должна гарантировать установку двух шрифтов: MT Extra и Fences, которые необходимы для набора математических символов. Таким же, абсолютно необходимым, является и шрифт Symbol, содержащий греческие буквы и базовые (далеко не все) математические знаки. Лично я дважды встречался с «умельцами», удалившими у себя на компьютере данный шрифт.

С точки зрения современных Windows-приложений принципиально важна возможность использовать шрифты Unicode, в которых отведен специальный диапазон для математических символов (шестнадцатеричные значения 2200–22FF). Только содержатся они в крайне немногих шрифтах, например, в «Arial Unicode MS», «MS Mincho» и др.

Подробности по всем вопросам использования Unicode можно уточнить на сайте www.unicode.org, а таблицы большинства спецсимволов размещены на странице Mathematical Operators.

Программа MathType, как более фундаментальная, содержит большой пакет дополнительных шрифтов. Их перечисление — довольно бессмысленная задача. Гораздо важнее то, что компания Design Science разрешает бесплатно установить полный шрифтовой комплект (18 математических шрифтов) на свой компьютер, так как он может потребоваться для просмотра формул. Архив располагается в Интернете (около 800 Мб для PostScript-шрифтов и около 900 Мб для TrueType-шрифтов). Ввод e mail необязателен!

Вместе с тем, возможно наиболее разумным следует признать установку 30-дневной пробной (trial) версии программы. В этом случае будут установлены все шрифты и полностью подключены все функции, часть из которых перестанет работать по окончании тестового срока. Но функциональность даже такой программы существенно выше, чем у Equation Editor.

Однако! После того, как срок истечет, все дополнительные функции будут заблокированы, а нажатие на новые горячие клавиши будет приводить к выводу весьма навязчивого сообщения о том, что теперь такая клавиша недоступна.

Источник