5.4 Измерение мощности в трёхфазных цепях
Активной мощностью трехфазной системы называют сумму активных мощностей ее отдельных фаз:

При симметричной нагрузке мощности отдельных фаз равны между собой, а общая мощность определяется как

На практике мощность трехфазной системы чаще выражают через линейные, а не через фазные токи и напряжения.

Для трехфазной системы также справедливы следующие соотношения для полной, активной и реактивной мощностей, соответственно:

Существуют несколько методов измерения мощности трехфазной системы, у каждого из них своя область применения.
Способ одного ваттметра.

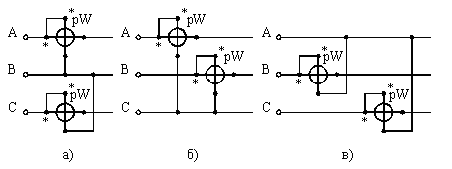
В этом случае общая мощность трехфазной системы равна утроенному показанию ваттметра:
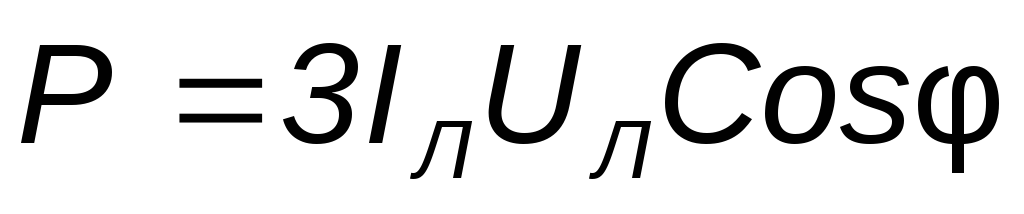
Способ трех ваттметров
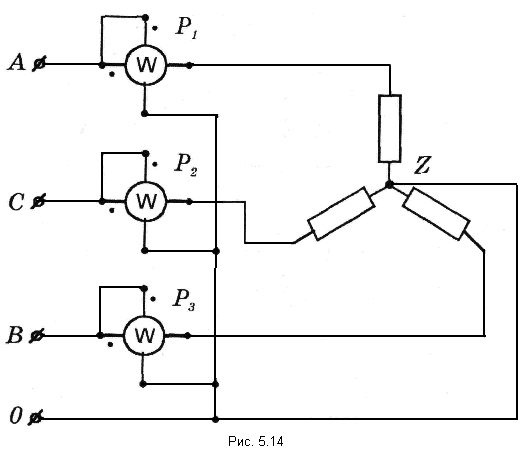
Активная мощность всей трёхфазной системы равна сумме показаний ваттметров:

3.Способ двух ваттметров.
Э
В этом случае общая мощность трехфазной системы равна алгебраической сумме показаний двух ваттметров.

5.5 Аварийные режимы
Аварийные режимы (обрыв, короткое замыкание) крайне нежелательны на практике, так как могут привести к поломке оборудования. Рассмотрим некоторые случаи аварийных режимов.
З
а) обрыв одной из фаз нагрузки, например фазы а (
В этом случае сопротивления фаз b и с включены последовательно, а токи в линейных проводах В и С

Напряжения фаз нагрузки становятся равными

Эту же электрическую цепь можно считать трёхфазной и вести расчёт, пользуясь формулой смещения (при этом 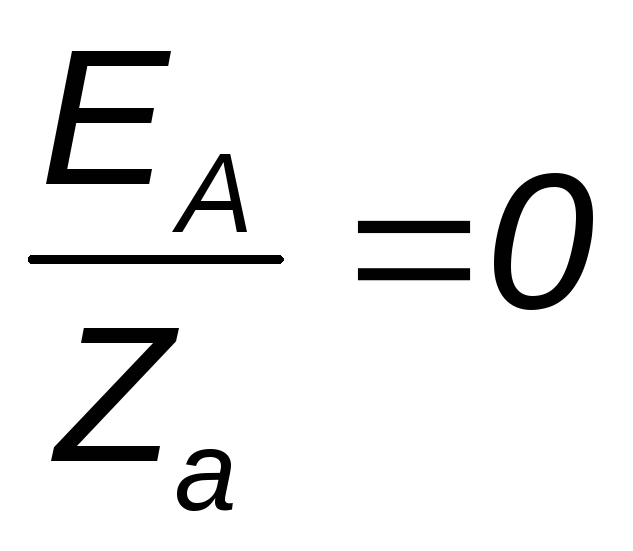



б) При коротком замыкании фазы нагрузки, например фазы а, (

Следовательно фазы нагрузки b и c находятся под соответствующими линейными напряжениями.
а
Для упрощения примем, что ZAB = ZCA = R, тогда

Независимо от режима AB напряжение на фазах нагрузки ZBC и ZCA остаётся неизменным.
б) при обрыве линейного провода, например провода А (рис. 5.17), схема преобразуется в однофазную. Для упрощения примем ZAB = ZBC = ZCA = R, тогда

Напряжение на фазах нагрузки AB и CA уменьшатся в два раза.
Для общего случая:


Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Как измерить мощность в цепи трехфазного переменного тока
Мощность в цепи трехфазного тока может быть измерена с помощью одного, двух и трех ваттметров. Метод одного прибора применяют в трехфазной симметричной системе. Активная мощность всей системы равна утроенной мощности потребления по одной из фаз.
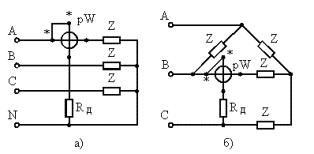
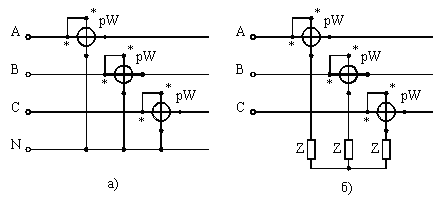
При соединении нагрузки звездой с доступной нулевой точкой или если при соединении нагрузки треугольником имеется возможность включить обмотку ваттметра последовательно с нагрузкой, можно использовать схемы включения, показанные на рис. 1.
Рис. 1 Схемы измерения мощности трехфазного переменного тока при соединении нагрузок а — по схеме звезды с доступной нулевой точкой; б — по схеме треугольника с помощью одного ваттметра
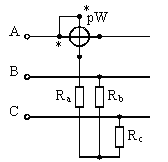
Если нагрузка соединена звездой с недоступной нулевой точкой или треугольником, то можно применить схему с искусственной нулевой точкой (рис. 2). В этом случае сопротивления должны быть равны Rвт+ Rа = Rb =Rc.
Рис 2. Схема измерения мощности трехфазного переменного тока одним ваттметром с искусственной нулевой точкой

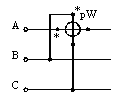
Рис. 3. Схема измерения реактивной мощности трехфазного переменного тока одним ваттметром

При измерении реактивной мощности можно применять схему рис. 5, а с искусственной нулевой точкой. Для создания нулевой точки необходимо выполнить условие равенства сопротивлений обмоток напряжений ваттметров и резистора R. Реактивная мощность вычисляется по формуле
где Р1 и Р2 — показания ваттметров.
По этой же формуле можно вычислить реактивную мощность при равномерной загрузке фаз и соединении ваттметров по схеме рис. 4. Достоинство этого способа в том, что по одной и той же схеме можно определить активную и реактивную мощности. При равномерной загрузке фаз реактивная мощность может быть измерена по схеме рис. 5, б.
Метод трех приборов применяется при любой нагрузке фаз. Активная мощность может быть замерена по схеме рис. 6. Мощность всей цепи определяется суммированием показаний всех ваттметров.
Рис. 4. Схемы измерения активной мощности трехфазного переменного тока двумя ваттметрами а — токовые обмотки включены в фазы А и С; б — в фазы А и В; в — в фазы В и С
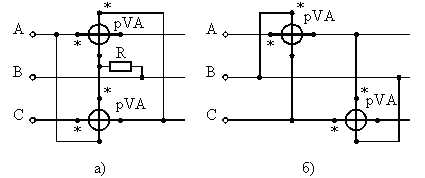
Реактивная мощность для трех- и четырехпроводной сети измеряется по схеме рис. 7 и вычисляется по формуле
где РA, РB, РC — показания ваттметров, включенных в фазы А, В, С.
Рис. 5. Схемы измерения реактивной мощности трехфазного переменного тока двумя ваттметрами
Рис. 6. Схемы измерения активной мощности трехфазного переменного тока тремя ваттметрами а — при наличии нулевого провода; б — с искусственной нулевой точкой
На практике обычно применяют одно-, двух- и трехэлементные трехфазные ваттметры соответственно методу измерения.
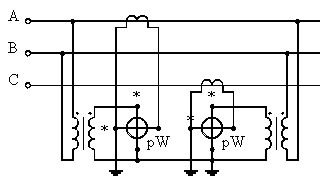
Чтобы расширить предел измерения, можно применить все указанные схемы при подключении ваттметров через измерительные трансформаторы тока и напряжения. На рис. 8 в качестве примера показана схема измерения мощности по методу двух приборов при включении их через измерительные трансформаторы тока и напряжения.
Рис. 8. Схемы включения ваттметров через измерительные трансформаторы.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Портал ТОЭ
4.10 Измерение мощности в трёхфазных цепях
1. При симметричной нагрузке мощность можно измерить одним ваттметром.
Мощность трёхфазной системы независимо от вида соединения нагрузки
Если нулевая точка не выведена, измерение производится с искусственной нулевой точкой.
Параллельная цепь ваттметра и два R доб , равные по величине R W , образуют искусственную нулевую (нейтральную) точку. Сопротивление ваттметра R W должно быть активным по характеру.
Для получения трёхфазной мощности показание ваттметра.
Для измерения реактивной мощности используется схема:
Для измерения мощности несимметричной системы используют три ваттметра.
В трёхпроводной системе мощность можно измерить с помощью двух ваттметров:
Для определения мощности трёхфазной системы показания двух ваттметров алгебраически складывают. Если стрелка одного из ваттметров отклоняется в другую сторону (влево), то изменив направление подводимого к ваттметру тока или напряжения и измерив показание ваттметра, значение этой мощности учитывается со знаком « − �.
Т.к. нейтральные точки источника и приёмника должны совпадать при использовании метода двух ваттметров, метод применим для симметричной нагрузки или при небольшой несимметрии.
При симметричном режиме показания ваттметров составят:
При φ = 60 ∘ , P 2 = 0 ,
при φ = − 60 ∘ , P 1 = 0 ,
при φ > 60 ∘ , P 2 0 .
Доказательство неприменимости метода двух ваттметров для измерения мощности несимметричной нагрузки.
Источник
Мощность трехфазной системы и методы ее измерения
Лекция № 3. Трехфазные электрические цепи
1. Понятие о трехфазных цепях и их преимущества.
2. Соединение звездой.
3. Соединение треугольником.
4. Мощность трехфазной системы и методы ее измерения.
Понятие о трехфазных цепях и их преимущества
Объединение в одной линии электропередачи нескольких цепей переменного тока с независимыми источниками электроэнергии называется многофазной системой. Наибольшее распространение получила трехфазная система, которая была изобретена и разработана во всех деталях, включая генератор трехфазного переменного тока, трехфазный трансформатор и асинхронный двигатель, русским инженером М.О. Доливо-Добровольским в 1889 – 1891 гг.
Трехфазной системой переменного тока называется совокупность трех однофазных переменных токов одинаковой частоты и амплитуды, сдвинутых друг относительно друга на 1/3 периода (3π/2 или 120°) [1, 2].
| Для того чтобы выяснить, как получают трехфазный переменный ток, рассмотрим устройство трехфазного генератора. Трехфазный генератор состоит из трех одинаковых, изолированных друг от друга обмоток, расположенных на статоре и разнесенных в пространстве на 120°. В центре статора вращается электромагнит (рис. 1.1). При этом форма магнита такова, что магнитный поток, пронизывающий каждую катушку, изменяется по косинусоидальному закону. Тогда по закону электромагнитной индукции в катушках будут |  Рис. 1.1. Схема трехфазного генератора Рис. 1.1. Схема трехфазного генератора |
индуцироваться ЭДС равной амплитуды и частоты, отличающиеся друг от друга по фазе на 120° (1-3) [1]:
 , (1); , (1); |  , (2); , (2); | 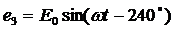 , (3). , (3). |
Эти три ЭДС можно изобразить на временной (рис.1.2 а), и векторной (рис.1.2 б) диаграммах [1].
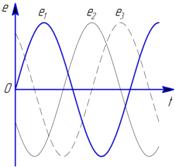 а а |  б б |
Рис. 1.2. Временная и векторная диаграммы
Как видно из векторной диаграммы (рис.1.2. б), сумма этих трех ЭДС равна нулю. Если в трехфазной системе действуют электродвижущие силы, равные по величине и сдвинутые по фазе на 120°, а полные сопротивления нагрузок всех трех фаз как по величине, так и по характеру (по величине и знаку фазового сдвига) одинаковы, то режим в ней называется симметричным. Невыполнение одного из этих условий или обоих вместе является причиной несимметричного режима [1].
Для получения трехфазной системы, необходимо определенным образом соединить ее цепи. Существуют два основных способа соединения: звездой и треугольником [1].
Соединение звездой
Отдельные фазы трехфазной системы принято обозначать латинскими буквами А, В и С. Этими же буквами обозначают начала обмоток генератора. Концы обмоток обозначают буквами X, Y и Z.
Условимся, что положительно направленный ток выходит из обмотки генератора через ее начало и входит в нее через ее конец (рис. 1.3). Если все концы обмоток генератора соединить в одной точке О, а к их началам присоединить провода, идущие к приемникам электрической энергии (у которых концы также соединены в общей точке О’), то мы получим соединение звездой (рис. 1.3) [1]:
 Рис. 1.3. Соединение звездой Рис. 1.3. Соединение звездой | 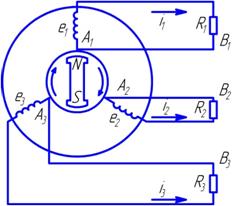 Рис. 1.1. Схема трехфазного генератора Рис. 1.1. Схема трехфазного генератора |
Мы видим, что контуры, по которым замыкаются фазные токи, при таком соединении не изменятся по сравнению с рисунком 1.1. Следовательно, по общему обратному проводу будет протекать ток, равный сумме токов трех фаз (4) [1]:

Если все три фазы имеют одинаковые нагрузки, то фазные токи будут равны по модулю, отличаясь друг от друга по фазе на 120° (5, 5.1, 5.2) [1]:
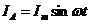 , (5) , (5) |  , (5.1) , (5.1) |  Рис. 1.4. Векторная диаграмма Рис. 1.4. Векторная диаграмма |
В цепях трехфазного тока вне зависимости от способа соединения различают два типа напряжений – линейные Un и фазные Uф – и два типа токов – линейные Iл и фазные Iф. Напряжение между двумя линейными проводами называется линейным, а между линейным и нулевым проводом – фазным. Токи, протекающие в линейных проводах, называются линейными, а в нагрузках фаз – фазными.
На первый взгляд может показаться, что поскольку в нулевом проводе ток равен нулю, то этот провод можно совсем убрать, оставив только три линейных провода. Однако, это не всегда возможно. В случае несимметричной нагрузки отсутствие нулевого провода приведет к перераспределению фазных напряжений, в результате чего некоторые из них станут выше номинального (что недопустимо), а некоторые – ниже. Если же при несимметричной нагрузке включить нулевой провод, то все фазные напряжения будут равны номинальному, а по нулевому проводу будет протекать некоторый ток. В этом легко убедиться с помощью векторных диаграмм. Следовательно, в цепях с симметричными нагрузками нулевой провод не нужен. Таковыми являются, например, электродвигатели. Однако, наличие нулевого провода обеспечивает равенство фазных напряжений при несимметричной нагрузке.
В дальнейшем для обозначения линейных напряжений будем пользоваться двойными индексами, а фазных – одинарными (рис. 1.5).
Рис. 1.5. Схема напряжений
При соединении звездой линейный ток совпадает с фазным, т.е. Iл = Iф. Как видно (рис. 1.5), линейные напряжения при соединении звездой являются векторными разностями соответствующих фазных напряжений (6, 6.1, 6.2) [1]:
 , (6); , (6); | 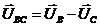 , (6.1); , (6.1); |  , (6.2). , (6.2). |
Построим векторную диаграмму линейных и фазных напряжений при соединении звездой (рис. 1.6).
Сначала построим три вектора фазных напряжений   и и  , расположенные друг относительно друга под углом 120º, а затем, пользуясь соотношениями (6 – 6.2) векторы линейных напряжений. Для построения вектора линейного напряжения , расположенные друг относительно друга под углом 120º, а затем, пользуясь соотношениями (6 – 6.2) векторы линейных напряжений. Для построения вектора линейного напряжения  нужно из вектора нужно из вектора 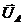 вычесть вектор вычесть вектор  , то есть прибавить к вектору , то есть прибавить к вектору 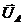 вектор вектор 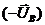 . Таким же способом строятся и остальные векторы линейных напряжений. Мы видим, что линейные напряжения также образуют симметричную трехлучевую звезду, повернутую относительно звезды фазных напряжений на угол 30° против часовой стрелки. . Таким же способом строятся и остальные векторы линейных напряжений. Мы видим, что линейные напряжения также образуют симметричную трехлучевую звезду, повернутую относительно звезды фазных напряжений на угол 30° против часовой стрелки. | 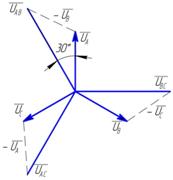 Рис. 1.6. Векторная диаграмма линейных и фазных напряжений при соединении звездой Рис. 1.6. Векторная диаграмма линейных и фазных напряжений при соединении звездой |
Для нахождения соотношения между модулями линейных и фазных напряжений рассмотрим тупоугольный треугольник с углом 120° при вершине, образованный векторами 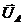
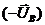

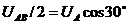

Таким образом, в трехфазной системе, соединенной звездой, линейные напряжения больше фазных в 

В России и в большинстве других стран напряжения 127, 220 и 380В приняты стандартными для приемников низкого напряжения. При соединении звездой с нулевым проводом существуют две системы напряжений – 220/127В и 380/220В. Наличие двух напряжений (линейного и фазного) является достоинством четырехпроводной линии.
Если при соединении звездой с нулевым проводом нагрузка становится неравномерной, то соотношение (7) можно считать практически справедливым. Следует только помнить, что в этом случае в нулевом проводе появляется ток. Это приводит к незначительному падению напряжения на нулевом проводе. Поэтому можно считать, что между нулевой точкой генератора и нулевой точкой приемника разность потенциалов отсутствует.
Соединение звездой без нулевого провода применяют при подключении обмоток трехфазных двигателей, а соединение с нулевым проводом при электрификации жилых домов. В последнем случае он необходим, т.к. в жилом доме практически невозможно добиться симметрии нагрузок. При этом к домам подводят три фазы и нулевой провод, а внутри каждого дома стремятся примерно одинаково загрузить каждую из фаз, чтобы общая нагрузка была более или менее симметричной. К каждой квартире подводят нулевой провод и одну из фаз. Установка предохранителей в нулевом проводе на распределительных щитах категорически запрещена, так как при его перегорании фазные напряжения могут стать неравными, а это приводит к превышению номинального напряжения в некоторых фазах и выходу из строя осветительных и бытовых приборов.
Соединение треугольником
Если обмотки генератора трехфазного тока соединить так, что конец первой обмотки соединяется с началом второй, конец второй с началом третьей, конец третьей с началом первой, а к общим точкам подключить линейные провода, то получим соединение треугольником (рис. 1.7).
Рис. 1.7. Соединение треугольником
Кажущегося короткого замыкания в обмотках генератора не произойдет, так как сумма мгновенных значений ЭДС в них равна нулю (8), в чем легко убедиться, построив векторную диаграмму [1]:

На рисунке 1.7 три приемника тока z1, z2, z3 также включены треугольником. В отличие от соединения звездой, где в большинстве случаев применяется четырехпроводная система, здесь используются три провода.
При соединении треугольником существуют только линейные напряжения (UAB,UBC,UCA), поскольку нулевой провод отсутствует, но появляются фазные (Iab,Ibc, Ica) и линейные (IА, IВ, IС) токи. Соотношения между линейными и фазными токами легко могут быть получены, если для каждой узловой точки потребителя применить первое правило Кирхгофа (9, 9.1, 9.2) [1]:
 , (9); , (9); | 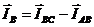 , (9.1); , (9.1); |  , (9.2). , (9.2). |
Из этих соотношений видно, что любой из линейных токов равен геометрической разности двух фазных токов. Кроме того, почленное сложение этих равенств показывает, что геометрическая сумма линейных токов равна нулю (10) [1]:

Для построения векторной диаграммы в качестве исходных возьмем три вектора линейных напряжений (UAB,UBC ,UCA ), расположенные под углом 120° друг относительно друга (рис. 1.8). При симметричной нагрузке векторы фазных токов IАВ ,IBC, IСА сдвинуты по фазе относительно соответствующих напряжений на угол φ, величина которого зависит от характера нагрузки [1].
Теперь, пользуясь соотношениями (9 – 9.2), построим на этой же диаграмме векторы линейных токов. Для того чтобы построить вектор линейного тока  , нужно к вектору фазного тока , нужно к вектору фазного тока  прибавить вектор ( прибавить вектор ( 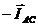 ), то есть вектор, равный по длине ), то есть вектор, равный по длине  , но противоположный по направлению. Так же строятся остальные векторы линейных токов. Для нахождения соотношения между модулями линейных и фазных токов рассмотрим тупоугольный треугольник с углом 120° при вершине, образованный векторами , но противоположный по направлению. Так же строятся остальные векторы линейных токов. Для нахождения соотношения между модулями линейных и фазных токов рассмотрим тупоугольный треугольник с углом 120° при вершине, образованный векторами  , ( , (  ) и ) и  . Опустим перпендикуляр из . Опустим перпендикуляр из |  Рис. 1.9. Векторная диаграмма линейных и фазных напряжений при соединении треугольником Рис. 1.9. Векторная диаграмма линейных и фазных напряжений при соединении треугольником |
вершины тупого угла этого треугольника на противоположную сторону и найдем (11) [1]:

Следовательно (12) [1]:

Таким образом, в трехфазной системе, соединенной треугольником, линейные токи больше фазных в раз, а фазные напряжения совпадают с линейными. Наличие двух способов включения нагрузок расширяет возможности потребителей. Например, если каждая из трех обмоток трехфазного электродвигателя рассчитана на напряжение 220В, то электродвигатель может быть включен треугольником в сеть 220/127В или звездой в сеть 380/220В. Соединение треугольником чаще всего используется в силовых установках (электродвигатели и т. п.), где нагрузка близка к равномерной. В трехфазных цепях способ включения нагрузки (звездой или треугольником) не зависит от способа включения обмоток генератора или трансформатора, питающего данную цепь.
Мощность трехфазной системы и методы ее измерения
Активной мощностью трехфазной системы называют сумму активных мощностей ее отдельных фаз (13) [1]:
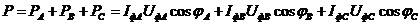
При симметричной нагрузке мощности отдельных фаз равны между собой, а общая мощность определяется как (14) [1]:
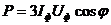
На практике мощность трехфазной системы чаще выражают через линейные, а не через фазные токи и напряжения. При соединении звездой 


Для трехфазной системы также справедливы следующие соотношения для полной, активной и реактивной мощностей, соответственно (16, 16.1, 16.2) [1]:
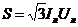 , (16); , (16); | 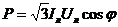 , (16.1); , (16.1); |  , (16.23). , (16.23). |
Существуют несколько методов измерения мощности трехфазной системы, у каждого из которых своя область применения. Для измерения мощности используются, в основном, однофазные ваттметры электродинамической системы.
Однофазный ваттметр (рис. 1.10) содержит две обмотки – токовую (обозначена более жирной линией), которая включается последовательно с объектом измерения (как амперметр), и обмотку напряжения, включаемую параллельно (как вольтметр).
| Рассмотрим измерение активной мощности. Для измерения активной мощности применяют четыре способа. 1. Способ одного ваттметра используют для измерения мощности при симметричной нагрузке, соединенной звездой с доступной нулевой точкой (рис. 1.11). При этом токовая цепь ваттметра включается последовательно с одной из фаз нагрузки, а цепь напряжения прибора – на напряжение этой же фазы. В этом случае общая мощность трехфазной системы равна утроенному показанию ваттметра (17) [1]: |  Рис. 1.10. Схема однофазного ваттметра Рис. 1.10. Схема однофазного ваттметра |
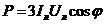
2. Способ одного ваттметра с созданием искусственной нулевой точки применяют тогда, когда нагрузка симметрична, а нулевая точка нагрузки недоступна или вообще отсутствует (например, при соединении треугольником). Токовая обмотка ваттметра включается последовательно в одну из фаз нагрузки, а нулевую точку создают путем включения двух одинаковых добавочных сопротивлений Rg между двумя другими фазами (рис. 1.12). Величина добавочных сопротивлений должна быть равна сопротивлению обмотки напряжения ваттметра. Тогда искусственная нулевая точка является нулевой точкой звезды, состоящей из сопротивления обмотки напряжения ваттметра и двух добавочных сопротивлений, и цепь напряжения ваттметра находится под фазным напряжением, а через токовую цепь проходит фазный ток. В этом случае общая мощность трехфазной системы равна утроенному показанию ваттметра.
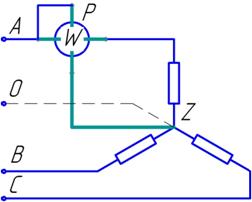 Рис. 1.11. Способ одного ваттметра Рис. 1.11. Способ одного ваттметра |  Рис. 1.12. Способ одного ваттметра с созданием искусственной нулевой точки Рис. 1.12. Способ одного ваттметра с созданием искусственной нулевой точки |
3. Способ трех ваттметров применяют для измерения мощности при неравномерной нагрузке, соединенной звездой. В каждый из линейных проводов включается токовая цепь одного из ваттметров, а их цепи напряжения включаются между соответствующим линейным проводом и нулевым проводом системы (рис. 1.13). При таком соединении каждый из ваттметров измеряет мощность одной фазы системы. Активная мощность всей трехфазной системы равна сумме показаний трех ваттметров.
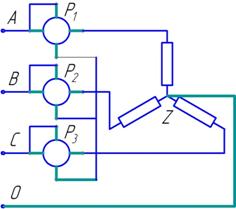 Рис. 1.13. Способ трех ваттметров Рис. 1.13. Способ трех ваттметров | 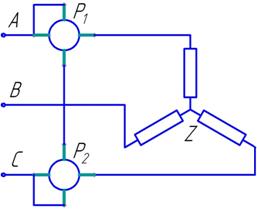 Рис. 1.14. Способ двух ваттметров Рис. 1.14. Способ двух ваттметров |
4. Способ двух ваттметров. Этот способ универсален – он применяется при симметричной и несимметричной нагрузках и при любом типе соединения. Нулевой провод может быть, а может и отсутствовать – он просто не используется. Токовые обмотки ваттметров включают в какие-нибудь две фазы, а обмотки напряжения между третьей (незанятой) фазой и той фазой, в которую включена токовая обмотка данного ваттметра (рис. 1.14).
В этом случае общая мощность трехфазной системы равна алгебраической сумме показаний двух ваттметров. Докажем это для случая соединения треугольником.
Общая мгновенная мощность трехфазной цепи при соединении треугольником равна сумме мгновенных мощностей отдельных фаз (18) [1]:

Дата добавления: 2018-05-12 ; просмотров: 2866 ; Мы поможем в написании вашей работы!
Источник



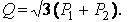
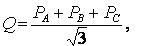
 , (5.2)
, (5.2)




