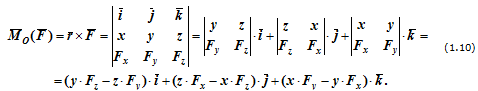iSopromat.ru
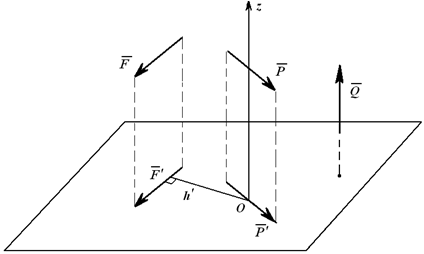
Момент силы относительно оси – это характеристика вращательного действия силы на тело, закрепленное на оси, т.е. алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 2).
Момент силы относительно, например, оси Oz (рисунок 1), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси ( F’) относительно точки пересечения оси с плоскостью, т.е.
Момент силы относительно оси – скалярная величина.
Моменты силы относительно координатных осей можно получить, расписав векторное произведение
Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.
Наш короткий видеоурок про момент силы с примерами:
Правило знаков
Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:
где FП – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П, h — плечо силы.
Это значит, что момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.
Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например Mz(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, Mz(Q).
Свойства момента силы относительно оси
Момент силы относительно оси обладает следующими свойствами:
- момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
- момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.
Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Лекция 3. Момент силы. Пара сил
3.1. Алгебраический момент силы на плоскости
Приложив силу к покоящемуся телу, можно сообщить ему поступательное движение. В таком режиме движения любая прямая, проведенная в теле, все время остается параллельной самой себе, а все точки тела движутся по одинаковым траекториям с одинаковыми скоростями. Тем самым, при таком движении осуществляется параллельный перенос тела на плоскости или в пространстве.
Пример. Поступательным является движение детали, помещенной на прямой участок ленты конвейера, или человека, стоящего на эскалаторе. Движение автомобиля на прямолинейном участке дороги также можно считать поступательным, если пренебречь вращением колес и вибрациями корпуса.
Однако в ряде случаев после приложения силы тело начинает вращаться – его точки двигаются по окружностям вокруг одной и той же точки или оси. Вращательный эффект силы харатеризуется ее моментом относительно точки или оси. Сначала изучим поворот тела под действием силы на плоскости, а затем обобщим полученные результаты на случай пространства.
Пусть к плоскому твердому телу приложена некоторая сила \(\vec F\). Ее алгебраическим моментом относительно заданной точки (полюса) O называется число, равное
| \(m_ | (3.1) |
Расстояние d от полюса до линии действия силы называется плечом силы относительно полюса O (рис. 3.1).
Рис. 3.1. Сила \(\vec F\) поворачивает тело вокруг полюса O. Положения тела до и после поворота отмечены сплошной линией и штрихом, соответственно
Знак «+» или «–» ставится в зависимости от того, в какую сторону сила пытается повернуть тело вокруг указанного полюса. Знаку «+» соответствует поворот против часовой стрелки, знак «–» выбирается при повороте по часовой стрелке. Так, при вычислении момента силы \(\vec F\) на рис. 3.1 следует выбрать знак «+».
Если плечо силы равно нулю, то ее момент относительно данного полюса также нулевой. Это понятно: сила, линия действия которой проходит через указанную точку, не может повернуть тело вокруг этой точки.
Поскольку в системе СИ сила измеряется в ньютонах, а расстояние – в метрах, то момент силы измеряется в ньютон-метрах (Н·м).
Изучая вращение тела вокруг точки на плоскости, можно считать, что мы имеем дело с вращением объемного тела вокруг некоторой оси и рассматриваем проекцию этого тела на плоскость, перпендикулярную оси.
Пример. Открываясь и закрываясь под действием приложенной силы \(\vec F\), дверь вращается вокруг вертикальной оси, проходящей через петли, соединяющие ее с косяком (рис. 3.2 а). Если сила перпендикулярна этой прямой, можно рассмотреть проекцию двери, ее оси вращения и силы на горизонтальную плоскость (рис 3.2 б). В этом случае вертикальная ось переходит в точку (полюс). Чтобы описать вращение двери, достаточно вычислить момент \(\vec F\) относительно этого полюса.
Рис. 3.2. Вычисление момента силы, приложенной к двери
Искомый момент зависит как от точки приложения силы (точнее – от расстояния l между нею и петлями), так и от угла α, образуемого линией действия силы с дверным полотном. Поскольку плечо силы d = l sin α, то ее момент (без учета направления вращения) составляет M = Fl sin α. Чем больше M, тем легче откроется дверь. Поэтому дверные ручки располагают как можно дальше от петель, увеличивая l (и M, соответственно). Если приложить силу непосредственно к петлям, то l = 0 и M = 0, поэтому дверь не повернется. При α = 0 линия действия силы также проходит через петли, M = 0 и дверь снова не сможет повернуться.
3.2. Момент силы в пространстве
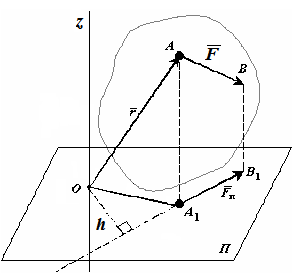
Моментом силы \(\vec F\) относительно точки O в пространстве будем называть вектор \(\vec m_
- Модуль искомого вектора равен произведению модуля силы на ее плечо относительно выбранного полюса O.
- Момент силы перпендикулярен плоскости, содержащей силу \(\vec F\) и точку O.
- При взгляде с конца \(\vec m_
(\vec F)\) поворот, осуществляемый с помощью силы \(\vec F\) вокруг полюса O, виден происходящим против часовой стрелки (рис. 3.3).
Рис. 3.3. Определение момента силы относительно точки в пространстве
Как видно, данное определение обобщает понятие алгебраического момента силы, введенное в предыдущем пункте. Оно содержит указание и на числовую величину момента, аналогичную плоскому случаю, и на плоскость, в которой происходит вращение, и на направление поворота. Напомним, что в формуле (3.1) это направление указывается знаком «+» или «–». Из определения следует также, что вектор \(\vec m_
Пусть \(\vec r\) – радиус-вектор, соединяющий полюс и точку приложения силы. Докажем, что тогда момент силы \(\vec F\) относительно полюса можно вычислить по формуле:
| \(\vec m_ | (3.2) |
Доказательство. Проверим, что вектор \(\vec m_
Угол между \(\vec r\) и \(\vec F\), если откладывать их от одной точки, равен 180°–α (см. рис. 3.3), поэтому модуль их векторного произведения mO = rF sin(180°–α) = rF sin α. Однако d = r sin α – это расстояние от линии действия силы \(\vec F\) до полюса O, т.е. плечо силы. Тем самым, числовое значение вектора \(\vec m_
Далее, по свойствам векторного произведения, \(\vec r\times\vec F\) перпендикулярен обоим векторам \(\vec r\) и \(\vec F\). Тем самым, он перпендикулярен плоскости, содержащей \(\vec F\) и O.
Наконец, тройка векторов \(\vec r\), \(\vec F\) и \(\vec m_
Как известно, векторное произведение равно нулю, если его сомножители коллинеарны (в частности, один из них или оба сразу могут быть нулевыми). Но если \(\vec r\) и \(\vec F\) в формуле (3.2) коллинеарны, то линия действия \(\vec F\) проходит через точку O. Как и на плоскости, сила, чья линия действия проходит через полюс, не может повернуть тело вокруг него.
Пусть в пространстве введена система координат Oxyz с центром в полюсе O, и в этой системе векторы \(\vec r\) и \(\vec F\) имеют следующие координаты: \(\vec r=\
\begin | (3.3) | |
Выражения (3.3) можно не запоминать: достаточно помнить равенство (3.2) и уметь вычислять векторное произведение в координатах.
Пример. Сила \(\vec F=\<3;8;5\>\) приложена к точке A(2; 0; –1). Найти числовую величину момента силы относительно точки B(4; –3; 3).
Сначала найдем вектор момента силы, а потом его модуль. Воспользуемся формулой (3.2), в которую вместо \(\vec r\) подставим вектор \(\overrightarrow
$$ \vec r\times\vec F= \begin
Длина этого вектора равна \(\sqrt<47^<2>+(-2)^<2>+25^<2>>=\sqrt<2838>\approx 53.27\). Итак, числовая величина момента силы составляет приближенно 53.27 Н·м (если сила в задаче измеряется в ньютонах, а расстояние – в метрах).
Выше было сказано, что приложенная сила пытается повернуть тело вокруг оси, которая перпендикулярна плоскости, содержащей полюс и сам вектор силы. Однако в принципе можно изучить вращение тела вокруг произвольной оси l, проходящей через выбранный полюс O. Для этого вводят числовую величину, называемую моментом силы относительно оси, проходящей через полюс. По определению, она равна проекции момента силы относительно этого полюса на указанную ось. Тем самым, формулы (3.3) выражают моменты силы \(\vec F\) относительно координатных осей через ее компоненты и координаты ее точки приложения.
Выясним, каков смысл введенного понятия. Пусть через точку O проведена ось l, сила \(\vec F\) приложена к точке A и вектор \(\overrightarrow
Рис. 3.4. Определение момента силы относительно оси
Разложим векторы \(\vec r\) и \(\vec F\) на составляющие, параллельные и перпендикулярные проведенной оси: \(\vec r=\vec r_<||>+\vec r_<\perp>\), \(\vec F=\vec F_<||>+\vec F_<\perp>\) (рис. 3.4 б). Подставим эти выражения в (3.2) и раскроем скобки:
$$ \vec r\times\vec F=(\vec r_<||>+\vec r_<\perp>)\times(\vec F_<||>+\vec F_<\perp>)=\vec r_<||>\times\vec F_<||>+ \vec r_<||>\times\vec F_<\perp>+\vec r_<\perp>\times\vec F_<||>+\vec r_<\perp>\times\vec F_<\perp>. $$
Векторы \(\vec r_<||>\) и \(\vec F_<||>\) параллельны l, а значит, коллинеарны друг другу. Поэтому их векторное произведение равно нулю. Далее используем тот факт, что векторное произведение перпендикулярно каждому из своих сомножителей. Значит, второе слагаемое перпендикулярно \(\vec r_<||>\), а третье – \(\vec F_<||>\). Поскольку указанные векторы параллельны l, то оба слагаемых образуют с этой осью угол 90°, а значит, их проекции на нее равны нулю. Остается разобраться лишь со слагаемым \(\vec r_<\perp>\times\vec F_<\perp>\).
И \(\vec r_<\perp>\), и \(F_<\perp>\) лежат в плоскости, перпендикулярной l, поэтому \(\vec r_<\perp>\times\vec F_<\perp>\) параллелен данной оси. Следовательно, длина этого вектора (с учетом знака) и будет искомым моментом силы. Перейдем в плоскость, где лежат \(\vec r_<\perp>\) и \(\vec F_<\perp>\); без ограничения общности можно считать, что она проходит через точку O (рис. 3.4 в). Модуль \(\vec r_<\perp>\times\vec F_<\perp>\) равен r⊥F⊥sin α. Однако (ср. с рассуждениями после формулы (3.2)) d = r⊥sin α – это плечо силы \(\vec F_<\perp>\) относительно точки O, т.е. по модулю искомый момент равен F⊥d.
Выясним знак проекции \(\vec r\times\vec F\) на l. Предположим, что рис. 3.4 в) изображает положение векторов и точек, видимое с положительного направления оси. Мысленно отложим \(\vec r_<\perp>\) и \(\vec F_<\perp>\) от одной точки, например, от полюса O. Если теперь кратчайший поворот от первого вектора ко второму осуществляется против часовой стрелки, то векторное произведение \(\vec r_<\perp>\times\vec F_<\perp>\) направлено в сторону наблюдателя, а значит, проекция \(\vec r\times\vec F\) на ось положительна. С другой стороны, нетрудно видеть, что в этом случае \(\vec F_<\perp>\) пытается повернуть тело против часовой стрелки вокруг точки O и оси l. Аналогично, если кратчайший поворот от \(\vec r_<\perp>\) к \(F_<\perp>\) происходит по часовой стрелке, то проекция \(\vec r\times\vec F\) на l отрицательна, а \(\vec F_<\perp>\) поворачивает тело вокруг O по часовой стрелке. Этот результат можно сравнить с формулой (3.1).
Обобщим вышесказанное. Модуль искомого момента равен произведению силы \(\vec F_<\perp>\) на ее плечо, а знак определяется направлением возможного вращения вокруг l. Тем самым,
Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси и плоскости.
Из наших рассуждений вытекает, что момент силы относительно оси равен нулю в двух случаях:
- Когда линия действия силы проходит через ось. В этом случае равно нулю плечо силы.
- Когда сила параллельна оси. Так, в формуле (3.3) для момента относительно оси Oz присутствуют только x— и y-проекции силы \(\vec F\), т.е. роль играют ее компоненты, перпендикулярные Oz. Повернуть тело вокруг оси, прикладывая силу в пареллельном направлении, невозможно.
Конечно, здесь и выше предполагается, что приложенная к телу сила \(\vec F\) сама не равна нулю.
Пример. На ось ординат надет тонкий абсолютно твердый диск радиуса R; его центр находится на расстоянии a от начала координат. К верхней точке диска параллельно горизонтальной плоскости Oxy приложена сила \(\vec F=\
Вычислим момент силы \(\vec F\) относительно начала координат O, а затем найдем проекции найденного вектора на оси Ox, Oy, Oz. Радиус-вектор точки приложения силы равен \(\vec r=\<0;a;R\>\), поэтому
$$ \vec m_
Следовательно, искомые моменты равны \(m_
Конечно, можно было бы сразу применить равенства (3.3). Но, как уже было сказано, лучше не запоминать дополнительно три формулы, а пользоваться одной – (3.2).
Полученный результат можно проверить и другим способом: вычисляя не векторное произведение, а моменты силы относительно осей. Для этого спроецируем чертеж на координатные плоскости и рассмотрим эти проекции, глядя со стороны положительных направлений осей координат (рис. 3.6).
При взгляде с конца оси Ox мы увидим лишь силу Fy, как на рис. 3.6 а). Ее плечо, очевидно, равно R, причем она пытается повернуть тело по часовой стрелке. Значит, момент \(\vec F_
3.3. Пара сил
Пара сил (или просто пара) – это система двух сил, равных по модулю и противоположных по направлению. Расстояние d между линиями действия этих сил называется плечом пары (рис. 3.7), а плоскость, в которой лежат обе силы, – плоскостью действия пары (или просто плоскостью пары).
Рис. 3.7. Пара сил и плечо пары
Пара сил не имеет равнодействующей (этот факт будет доказан позднее). Исключением является случай, в котором плечо пары равно нулю: тогда линии действия сил совпадают и система оказывается уравновешенной. Далее мы будем считать, что плечо пары не равно нулю.
Приложенная к телу пара пытается повернуть его в плоскости, в которой лежат обе силы, составляющие эту пару. Указанное свойство используют для управления движением тел.
Пример 1. При отворачивании болтов, которыми автомобильное колесо крепится к ступице, применяют баллонный ключ, в ряде случаев имеющий форму креста. Чтобы повернуть ключ, силы прикладывают к двум противоположным лучам креста, надетого на головку болта (рис. 3.8).
Рис. 3.8. Баллонный ключ: а) общий вид; б) применение
Пример 2. Если самолету, оснащенному двумя двигателями, требуется развернуться на рулежной дорожке аэродрома, один из них включают в режиме прямого хода, а другой – в режиме реверса (рис. 3.9).
Рис. 3.9. Разворот самолета на рулежной дорожке
Будучи неконтролируемым, эффект вращения тела под действием пары может привести к отрицательным и даже трагическим последствиям.
Пример. 9 июля 2006 г. в Иркутске при заходе на посадку потерпел крушение аэробус А310. При приземлении правый двигатель работал в режиме реверса, а левый по случайности был переведен в режим прямой тяги. В результате самолет закрутило на скользкой взлетно-посадочной полосе, он выкатился за ее пределы и столкнулся с гаражным массивом. Погибло 124 человека из 203, находившихся на борту.
Вращательный эффект пары характеризуется ее моментом. Описывая эффект на плоскости (см. рис. 3.7), вычисляют алгебраический момент пары:
Здесь F – модуль любой из сил, составляющих пару, d – ее плечо. Как и в (3.1), знак «+» выбирается, если поворот под действием пары происходит против часовой стрелки, знак «–» – при повороте по часовой стрелке.
Момент пары в пространстве – это вектор \(\vec m\), перпендикулярный плоскости пары. Его длина равна Fd, аналогично (3.4), а направление выбирается так, чтобы при взгляде с конца вектора поворот тела под действием пары происходил против часовой стрелки (рис. 3.10).
Рис. 3.10. Момент пары в пространстве
Пример. На судно в водоеме действуют две силы – тяжести \(\vec G\) и Архимеда \(\vec A\), причем первая прикладывается к центру тяжести всего судна, а вторая – к центру тяжести его подводной части. В стоячей воде эти силы разделяют общую (вертикальную) линию действия, они равны по модулю и противоположны по направлению, так что судно находится в равновесии (рис. 3.11 а). При бортовой или килевой качке форма подводной части судна меняется, а линии действия \(\vec G\) и \(\vec A\) смещаются друг относительно друга. На рис. 3.11 б) показан эффект бортовой качки. В результате образуется пара; если ее момент будет достаточно большим, судно может опрокинуться.
Рис. 3.11. Судно в стоячей воде и эффект бортовой качки
Так, в 1628 г. при выходе из гавани Стокгольма потерпел крушение шведский корабль «Vasa». Он нес большое количество тяжелых орудий, а его мачты и бортовые надстройки были слишком высоки. Из-за этого его центр тяжести сместился вверх, плечо пары, образованной силами \(\vec G\) и \(\vec A\) при качке, оказалось большим, а момент превысил допустимое значение. В результате корабль перевернулся и затонул (рис. 3.12).
Рис. 3.12. Крушение корабля «Vasa»
В 1545 г. по аналогичным причинам погиб английский корабль «Mary Rose».
Выше была получена формула для расчета момента силы относительно точки в пространстве. Оказывается, пара сил имеет аналогичное свойство: момент пары равен моменту одной из ее сил относительно точки приложения другой силы (рис. 3.13).
Указанное свойство выражается равенством
| \(\vec m=\overrightarrow | (3.5) |
Его обоснование полностью аналогично доказательству формулы (3.2) и поэтому не приводится.
Формулу (3.5) можно обобщить с помощью следующей теоремы.
Теорема (о сумме моментов сил, составляющих пару). Какая бы точка ни была выбрана в качестве полюса, момент пары равен сумме моментов сил, ее составляющих, относительно этого полюса.
Доказательство. Пусть силы \(\vec F\) и \(\vec F’\), приложенные в точках A и A’, образуют пару. Выберем произвольную точку O (рис. 3.14) и найдем сумму моментов \(\vec F\) и \(\vec F’\) относительно нее.
Получим \(\vec m_
$$ \vec m_
Согласно (3.5), последнее выражение и есть искомый момент пары. Теорема доказана.
В завершение отметим, что выбранный полюс O не обязан лежать в плоскости действия пары.
Равенство (3.5) получается из этой теоремы как частный случай: достаточно в качестве полюса выбрать точку приложения одной из сил, составляющих пару.
Заделка. Теперь, имея представление о паре сил, можно изучить еще один вид связи – заделку, препятствующую вращению тела. Различают жесткую и скользящую заделку.
Замечание. Существует также свободная (бискользящая) заделка, но она встречается реже.
Жесткая заделка (или защемление) полностью запрещает любое движение тела – как поступательное, так и вращательное. Поэтому ее реакция описывается силой с неизвестными заранее модулем и направлением и парой с неизвестным моментом, который называют опорным. Тем самым, на плоскости реакция жесткой заделки описывается тремя параметрами: два из них отвечают за силовую часть реакции (например, ее проекции на координатные оси), третий – это алгебраический опорный момент (рис. 3.15 а). Жесткую заделку в пространстве описывают шесть параметров: три компоненты силовой реакции и три компоненты момента пары (рис. 3.15 б). При этом силы прикладываются в точке крепления («заделывания») тела.
Рис. 3.15. Реакция жесткой заделки
В реальности со стороны закрепленного конца на тело действует распределенная нагрузка: опорные реакции распределяются по некоторой площади, поскольку осуществить жесткое крепление в единственной точке технически невозможно. Однако эта нагрузка приводится к выбранной точке закрепления и заменяется сосредоточенной силой и парой.
Пример 1. Можно считать, что вбитая в землю свая фундамента связана с помощью жесткой заделки (рис. 3.16). Действительно, ее крепление должно быть таким, чтобы сваю было невозможно сместить в сторону от первоначального местоположения, вытащить из земли или повернуть. Грунт, окружающий сваю, оказывает давление на всю поверхность соприкосновения с ней, так что создаваемая им нагрузка, действительно, является распределенной.
Пример 2. Во многих случаях крепление плиты балкона к наружной несущей стене дома (рис. 3.17) также можно считать жесткой заделкой. Если рассмотреть «вид сбоку» и перейти от пространственной задачи к плоской, то получаемая картина аналогична рис. 3.15 а).
Горизонтальную балку с одним жестко защемленным концом называют консольной балкой (или просто консолью).
Скользящая заделка (ее также называют защемляющей подвижной) позволяет телу двигаться в одном направлении. Соответственно, в указанном (продольном) направлении эта связь не развивает реакцию (рис. 3.18).
Рис. 3.18. Реакция скользящей заделки
Поэтому на плоскости число параметров, описывающих данную связь, снижается по сравнению с жесткой заделкой с 3 до 2 (поперечная реакция и опорный момент), а в пространстве – с 6 до 5 или 4.
Пример. Представление о скользящей заделке в пространстве дают направляющие шпингалета (рис. 3.19). Они позволяют задвижке перемещаться по продольной оси и вращаться вокруг нее же. Соответственно, реакция направляющих задается четырьмя параметрами: двумя поперечными силовыми реакциями и двумя опорными моментами относительно осей, перпендикулярных задвижке.
3.4. Свойства пар
Произвольная пара сил в пространстве обладает такими свойствами:
- Не меняя действия пары на твердое тело, ее можно переносить куда угодно в ее плоскости действия (в том числе и поворачивать линии действия ее сил в этой плоскости).
- Можно менять плечо и модуль сил пары, сохраняя ее момент, при этом ее действие на твердое тело не изменится.
- Действие пары на твердое тело не изменится, если перенести плоскость ее действия параллельно самой себе.
Доказательство. Сначала докажем первые два свойства. Нам требуется из данной пары получить другую, силы которой приложены вдоль других линий действия и имеют другую величину и направление, нежели исходные. При этом первоначальная и новая системы сил обязаны быть эквивалентными, а моменты пар – равными.
Пусть силы \(\vec F\) и \(\vec F’\), образующие пару, приложены вдоль прямых l и l’, и необходимо получить пару, у которой линии действия сил совпадают с прямыми m и m’ (рис. 3.20 а). Отложим \(\vec F\) и \(\vec F’\) от точек пересечения A и A’ этих прямых, а далее воспользуемся правилом параллелограмма и разложим каждую из этих сил в сумму двух: \(\vec F=\vec P+\vec Q\), \(\vec F’=\vec P’+\vec Q’\). При этом \(\vec P\) и \(\vec P’\) должны быть направлены вдоль прямой AA’, а \(\vec Q\) и \(\vec Q’\) – вдоль заданных прямых m и m’ (рис. 3.20 б).
Рис. 3.20. Изменение плеча пары и ее перенос в плоскости действия
Очевидно, векторы \(\vec P\) и \(\vec P’\), \(\vec Q\) и \(\vec Q’\) противоположны. При этом \(\vec P\) и \(\vec P’\) имеют общую линию действия и, согласно первой аксиоме статики, уравновешивают друг друга. Следовательно, исходная пара \(\vec F,\vec F’\) эквивалентна паре \(\vec Q,\vec Q’\), силы которой приложены вдоль заданных прямых (а значит, пара имеет заранее заданное плечо).
Осталось доказать, что две пары – первоначальная и вновь полученная – имеют один и тот же момент. Но момент пары \(\vec Q,\vec Q’\) равен \(\overrightarrow
Докажем теперь третье свойство. Предположим, что силы \(\vec F\) и \(\vec F’\), образующие пару, имеют линии действия l и l’, соответственно, и требуется перенести пару \(\vec F,\vec F’\) в другую плоскость, где линиями действия сил станут прямые m и m’ (рис. 3.21 а). Для этого воспользуемся второй аксиомой статики и присоединим к исходной системе еще четыре силы: \(\vec G,\vec H\), приложенные вдоль прямой m, и \(\vec G’,\vec H’\), приложенные вдоль m’. При этом векторы \(\vec F\) и \(\vec G\), \(\vec F’\) и \(\vec G’\) равны; \(\vec G\) и \(\vec H\), \(\vec G’\) и \(\vec H’\) уравновешивают друг друга (рис. 3.21 б).
Рис. 3.21. Перенос пары в параллельную плоскость
Силы \(\vec F’\) и \(\vec H\) равны по модулю и сонаправлены, поэтому они имеют равнодействующую \(\vec R\). Ее числовая величина R = 2F, направление совпадает с направлением \(\vec F\), а линия действия проходит через середину отрезка, соединяющего точки приложения \(\vec F’\) и \(\vec H\). Аналогично, равнодействующую \(\vec R’\) имеют \(\vec F\) и \(\vec H’\).
Понятно, что векторы \(\vec R\) и \(\vec R’\) равны по длине и противоположны по направлению. Линия действия у них общая: она проходит через центр симметрии параллелограмма, образованного точками приложения сил \(\vec F\), \(\vec F’\), \(\vec G\), \(\vec G’\), \(\vec H\), \(\vec H’\). Следовательно, силы \(\vec R\) и \(\vec R’\) компенсируют друг друга; поэтому уравновешенной является и система \(\vec F’,\vec H,\vec F,\vec H’\). Отбрасывая ее согласно второй аксиоме статики, мы получим, что исходная пара \(\vec F,\vec F’\) эквивалентна паре сил \(\vec G,\vec G’\), приложенных вдоль заданных прямых m и m’, лежащих в другой плоскости. Последнее из перечисленных свойств доказано.
Замечание. Тот факт, что две сонаправленные силы имеют равнодействующую, будет в общем виде доказан в Лекции 7. Пока же, для частного случая равных по модулю сил, можно ограничиться соображениями симметрии. Достаточно представить, что к концам твердого стержня приложены две одинаковые силы. Эффект будет таким же, если приложить сонаправленную им вдвое большую силу к середине стержня.
Перечисленные свойства пар можно объединить в одну теорему (по сути, она доказана выше).
Теорема (об эквивалентности пар). Пары сил с одинаковыми моментами эквивалентны.
Нельзя сказать, что вектор момента пары отложен от какой-либо точки или «привязан» к какой-либо оси; в отличие от момента силы, он вычисляется не относительно точки или оси, а «сам по себе». Единственная существенная характеристика пары – ее момент, причем этот вектор является свободным.
Итак, если к телу приложена одна пара сил, оно станет вращаться. Что произойдет, если приложенных пар будет несколько? Можно ли упростить эту систему сил? На эти вопросы отвечает следующее утверждение.
Теорема (о сложении пар). Система из нескольких пар, приложенных к твердому телу, эквивалентна одной паре с моментом, равным сумме моментов всех приложенных пар.
Доказательство. Пусть к телу приложены две пары, плоскости действия которых пересекаются по некоторой прямой (рис. 3.22 а). Выберем на этой прямой две точки A и B. Пользуясь предыдущей теоремой, заменим исходные пары на другие, эквивалентные им \(\vec F,\vec F’\) и \(\vec G,\vec G’\), причем так, что силы \(\vec F\) и \(\vec G\) будут отложены от точки A, а \(\vec F’\) и \(\vec G’\) – от точки B (рис. 3.22 б).
Рис. 3.22. Сложение пар
Согласно правилу параллелограмма, две силы, отложенные от одной точки, можно заменить одной равнодействующей: \(\vec F+\vec G=\vec R\), \(\vec F’+\vec G’=\vec R’\), причем \(\vec R\) и \(\vec R’\), очевидно, образуют пару. Тем самым, две пары \(\vec F,\vec F’\) и \(\vec G,\vec G’\) эквивалентны одной – \(\vec R,\vec R’\). Ее момент равен
$$ \overrightarrow
т.е. сумме моментов исходных пар. Тем самым, для двух пар теорема доказана.
При упрощении системы из трех и более пар можно сначала сложить две пары, затем к полученному результату прибавить третью и т.д.
Вопросы для самоконтроля
Какие из сил, изображенных на рис. 3.23, имеют положительный алгебраический момент относительно точки O, а какие – отрицательный?
Задачи к лекции
- Чтобы повернуть дверь, требуется преодолеть момент силы трения в ее петлях, равный 22 Н·м. Для этого к дверной ручке перпендикулярно прямой, проходящей через дверные петли и под углом 60° к дверному полотну прикладывается сила 30 Н. Откроется ли дверь, если ручка расположена на расстоянии 75 см от петель?
- Сила \(\vec F=\<3;0;-2\>\) приложена в точке A(6; 2; 5). Вычислить модуль ее момента и длину плеча относительно точки B(4; 4; 7). Компоненты силы даны в Н, координаты – в м.
Сила \(\vec F=\<5;-7\>\) приложена в точке A(3; 4). Вычислить ее алгебраический момент относительно точки B(1; 1). Компоненты силы даны в Н, координаты – в м.
Указание. Воспользоваться формулами (3.3). Учесть, что момент считается не относительно начала координат.
Ответы. 1. Нет; момент силы равен приближенно 19.49 Н. 2. \(2\sqrt<14>\approx 7.48\) Н·м; \(2\sqrt<14>\approx 2.08\) м. 3. –29 Н·м. 4. а) нет, силы не противоположны; б) да; в) нет, силы приложены вдоль одной прямой.
Источник