1. ЕДИНИЦЫ ИЗМЕРЕНИЯ
Единицей измерения момента инерции вращающейся части I является килограмм-метр в квадрате (кг × м 2 ).
2. МЕТОДЫ ОПРЕДЕЛЕНИЯ МОМЕНТА ИНЕРЦИИ
Для определения момента инерции применяются следующие методы:
2.1. Метод крутильных колебаний
Метод крутильных колебаний следует предпочтительно применять для определения момента инерции вращающихся частей электрических машин мощностью до 100 кВт.
Вращающуюся часть следует подвесить на струне металлической или из иного высокопрочного материала с изотропной структурой согласно черт. 1. Диаметр и длину струны выбирают так, чтобы период крутильных колебаний Т был не менее 1 с. Механическая прочность струны должна соответствовать массе вращающейся части. Точка подвеса должна находиться точно на ее оси вращения.
Вращающуюся часть следует подвергнуть крутильным колебаниям и определить их период Т. При этом одностороннее угловое отклонение должно составлять не более 25°.
Таким же образом и на той же струне следует определить период крутильных колебаний Тн эталона, момент инерции которого определяют расчетным путем.
Момент инерции исследуемой вращающейся части вычисляют по формуле
где I — момент инерции исследуемой вращающейся части, кг × м 2 ;
Iн — момент инерции эталона, кг × м 2 ;
Т — период колебаний исследуемой вращающейся части, с;
Тн — период колебаний эталона, с.
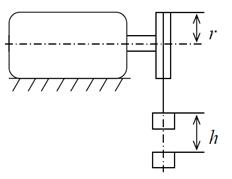
Эталон, момент инерции которого определен расчетным путем, может быть также закреплен на валу исследуемой вращающейся части, как показано на черт. 2. В этом случае момент инерции исследуемой вращающейся части следует определять по формуле
где I — момент инерции исследуемой вращающейся части, кг × м 2 ;
Iн — момент инерции эталона, кг × м 2 ;
Т — период колебаний исследуемой вращающейся части, с;
Tн — период колебаний исследуемой вращающейся части с эталоном, с.
Более тяжелые вращающиеся части могут быть подвешены на двух параллельных струнах, прикрепленных к вращающейся части симметрично относительно ее оси в соответствии с черт. 3. Длину струн l и расстояния от струн до оси вращающейся части r следует выбирать таким образом, чтобы период крутильных колебаний Т составлял не менее 1 с.
Вращающуюся часть необходимо подвергнуть крутильным колебаниям и измерить их период Т. Кроме того, надлежит определить массу вращающейся части m. Момент инерции исследуемой вращающейся части вычисляют по формуле
где I — момент инерции исследуемой вращающейся части, кг × м 2 ;
m — масса исследуемой вращающейся части, кг;
r — расстояния от струн до оси вращающейся части, м;
l — длина струн, м;
Т — период крутильных колебаний вращающейся части, с;
g = 9,81 м/с 2 — ускорение земного тяготения.
2.2. Метод вспомогательного маятника
Метод вспомогательного маятника может применяться для определения момента инерции вращающихся частей машин мощностью примерно от 10 до 1000 кВт. Для вращающихся частей, для которых также применим метод крутильных колебаний, последний является предпочтительным.
Вращающуюся часть следует установить на подшипниках балансировочного станка. Вращающиеся части с подшипниками качения могут быть установлены также на собственных подшипниках. Если испытание проводится в собранной машине, то в случае двигателей с фазным ротором и коллекторных машин следует поднять щетки.
Для определения момента инерции методом вспомогательного маятника следует прикрепить к валу исследуемой вращающейся части дополнительную массу mдоп посредством рычага, как показано на черт. 4. Эту массу следует выбрать таким образом, чтобы масса рычага была пренебрежимо малой по сравнению с дополнительной массой mдоп. Дополнительная масса может быть закреплена также на наружной поверхности самой вращающейся части, на шкиве или на полумуфте. Вспомогательный маятник должен быть рассчитан таким образом, чтобы период колебаний Т составлял от 3 до 8 с.
Вращающуюся часть совместно с прикрепленным к ней вспомогательным маятником приводят в колебания. При этом одностороннее угловое отклонение не должно быть более 15°. Период колебаний Т следует определить как средний из нескольких колебаний. Для обеспечения точности измерения периода колебаний его следует производить между моментами прохождения маятника через положение статического равновесия.
Момент инерции испытуемой вращающейся части следует определить по формуле
где mдоп — масса вспомогательного маятника, кг;
а — расстояние от центра тяжести вспомогательного маятника до оси вала вращающейся части, м;
Т — период колебаний маятника, с;
g = 9,81 м/с 2 — ускорение земного тяготения.
Для проверки полученного значения момента инерции опыт необходимо повторить с дополнительной массой другой величины.
Метод самоторможения может применяться для определения момента инерции вращающихся частей электрических машин мощностью свыше 100 кВт. Согласно этому методу машина с испытуемой вращающейся частью приводится во вращение с частотой выше номинальной при номинальном возбуждении или без него и затем отключается от источника питания. Для машин с фазным ротором и коллекторных машин испытание проводится с минимально необходимым количеством щеток, а остальные щетки надлежит поднять. После отключения определяется кривая самоторможения n = f(t) в диапазоне частоты вращения от 1,2nн до 0,8nн. Для достижения возможной точности при определении этой кривой снижение частоты вращения следует осциллографировать.
В соответствии с черт. 5 момент инерции I исследуемой вращающейся части для невозбужденной машины следует рассчитать по формуле
а для возбужденной машины по формуле:
где I — момент инерции вращающейся части, кг × м 2 ;
Рмех — механические потери при номинальной частоте вращения, Вт;
Рст — потери в стали при номинальной частоте вращения, Вт;
n н — номинальная частота вращения, об/мин;
D n — разность между верхним и нижним значениями частоты вращения в опыте, об/мин;
D t — время, в течение которого частота вращения машины изменяется на D n, с;
w н — номинальная угловая частота вращения, с -1 ;
D w — разность между верхним и нижним значениями угловой частоты вращения, с -1 .
За верхнюю точку частоты вращения принимается наивысшая возможная точка в опыте, но не менее 1,1nн. Нижняя точка должна отличаться от номинальной на такую же величину частоты вращения.
В случае невозможности повышения частоты вращения сверх номинального значения, вместо номинальной частоты вращения принимается частота вращения, лежащая на участке примерно от 0,9 до 0,8 номинальной частоты вращения. В этом случае потери должны быть измерены на данной частоте вращения.
Если для повышения частоты вращения машина должна быть соединена с приводным двигателем, который невозможно отсоединить на ходу, то в формулах ( 5 ) и (6) под потерями следует понимать потери всего агрегата. Из полученного таким образом момента I следует вычесть момент инерции вращающейся части приводного двигателя и соединительной муфты, подлежащей отдельному определению.
1. Автор — делегация ГДР в Постоянной Комиссии по стандартизации
3. Стандарт СЭВ утвержден на 40-м заседании ПКС
4. Сроки начала применения стандарта СЭВ:
Срок начала применения стандарта СЭВ в договорно-правовых отношениях по экономическому и научно-техническому сотрудничеству
Срок начала применения стандарта СЭВ в народном хозяйстве
Источник
Момент инерции для чайников: определение, формулы, примеры решения задач
- 12 января 2021 г.
- 7 минут
- 335 631
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Источник
Экспериментальные методы определения моментов инерции.



1) способ качений – используются для тел неправильной формы имеющих отверстия.
Тело подвешивают, определяют его положение центра тяжести, отклоняют из равновесного состояния и приводят в колебательное движение. Экспериментально определяют время τ , n – колебаний и Период Т=τ/n и находят Iz
2)Метод крутильных колебаний
Тело, момент инерции которого необходимо определить, подвешивается на упругом стержне, поворачивается на некоторый угол и отпускается. Начинаются крутильные колебания. Угол закручивания стержня связан с моментом следующим соотношением


3. способ падающего груза
Метод падающего груза. Недостатком описанных выше двух методов
определения момента инерции ротора является необходимость разборки
двигателя. Метод падающего груза позволяет определить момент инерции
На конце вала или шкива на валу навивают несколько витков гибкого
шнура. Другому концу шнура с прикрепленным к нему грузом дают воз-
можность опускаться (рис. 1.4). При эксперименте измеряют время t, за
которое груз опускается на высоту h. Момент инерции
Источник