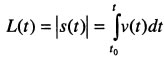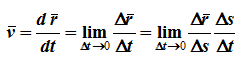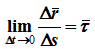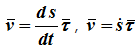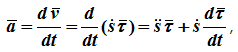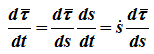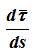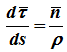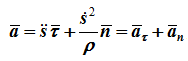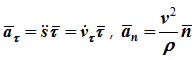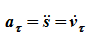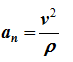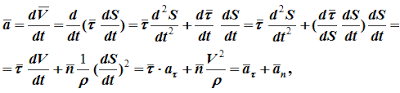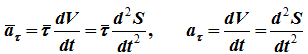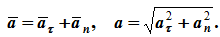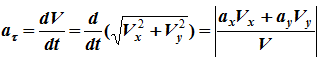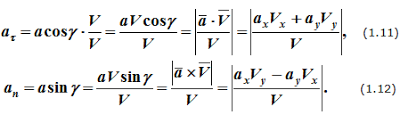Модуль ускорения точки при естественном способе задания движения определяется как

Содержание

Модуль ускорения точки при естественном способе задания движения определяется как
iSopromat.ru
iSopromat.ru
Скорость и ускорение точки
Ускорение точки при естественном способе задания движения
Ускорение точки при естественном способе задания движения

Модуль ускорения точки при естественном способе задания движения определяется как

3) Скорость и ускорение точки при естественном способе задания движения.

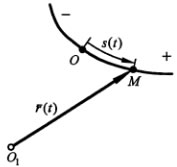
Если траектория точки известна (т.е. в некоторой системе отсчета определена графически, с помощью уравнения или другим образом), то задать движение точки можно естественным способом. Для этого необходимо: зафиксировать на трактории точку начала отсчета, выбрать положительное и отрицательное направления отсчета дуговой координаты и указать уравнение движения точки по траектории в виде S=S(t).

Скалярный параметр S в данном случае имеет смысл криволинейной (дуговой) координаты, модуль которой определяет текущее расстояние по траектории от начала отсчета (точки О) до подвижной точки М, а знак показывает, по какую сторону от начала отч=счета находится точка М на траектории.

Следует отметить, что уравнение движения в форме S=S(t) определяет текущее положение точки именно на траектории, при этом может быть установлена взаимно однозначная связь между значениями координаты S и радиус-вектором точки М в той системе отсчета, в которой определена в рассматриваемом случае траектория движения точки. Тогда радиус-вектор точки может быть представлен в виде функциональной зависимости от параметра S в виде r=r(S).

Модуль скорости, т.е. ее численное значение, при естественном способе задания движения точки определятся так: .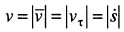

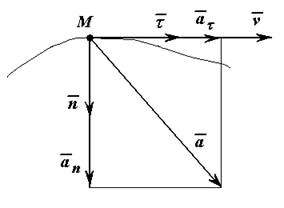
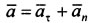
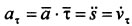
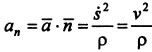
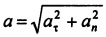
Ускорение составляет сумму касательной и нормальной составляющих: , где и . Следовательно: .

Дополнение: Значение пути —

Источник

iSopromat.ru

Рассмотрим определение скорости и ускорения точек при естественном способе задания движения:

— единичный вектор касательной, тогда

Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.

Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

поскольку τ — переменный по направлению вектор, то:

определяется только свойствами траектории в окрестности данной точки, при этом

n — единичный вектор главной нормали,
ρ — радиус кривизны траектории в данной точке.

т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:

алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

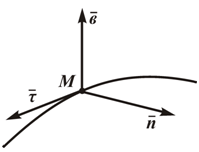
При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

τ — орт касательной;
n — орт нормали;
b — орт бинормали;

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Чтобы задать закон движения точки естественным способом необходимо:

знать траекторию движения;
установить начало отсчета на этой кривой;
установить положительное направление движения;
дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).

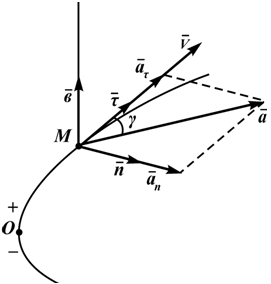
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

Скорость и ускорение точки

Скорость точки при естественном способе задания её движения определяется по формулам

Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

Ускорение определяется как производная от вектора скорости:

оно характеризует быстроту изменения величины скорости точки;

Нормальное ускорение точки

характеризует быстроту изменения направления вектора скорости;

ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).

Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):

Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

Далее, для естественнго способа задания движения точки, получаем

Источник

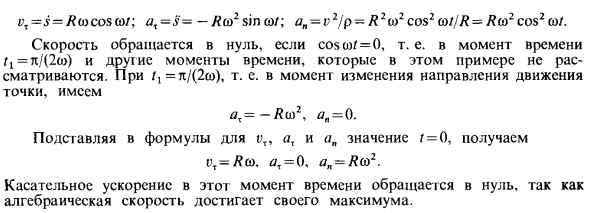
Ускорение точки при естественном способе задания движения

Для точечной скорости, Согласно определению ускорения. Мы получаем Это связано с тем, что y2 = n2 и dx / dz ориентированы на вогнутой поверхности траектории параллельно главному нормальному единичному вектору. Разлагает точечные ускорения вдоль оси естественного трехгранника. Блок ускорения at = ST = (dut / dz) T. Это называется тангенциальной составляющей ускорения. Другие части ускорения a „= (c2 / p) n = (s2 / p>. Это называется нормальной составляющей ускорения.

Он ориентирован внутри вогнутой поверхности траектории, то есть в положительном направлении единичного вектора основной нормали l. Это потому, что полное ускорение направлено внутрь вогнутой поверхности орбиты. Следовательно, ускорение очков Из (17) получим формулу для проекции ускорения на естественную ось. У нас есть: a, = s = dvt / dT, a = tr / p, ab = 0. (19) Проекция ускорения в направлении касательной, которая совпадает с направлением единичного вектора m, называется тангенциальным ускорением и является нормальным ускорением ускорения на главной нормали, направленной вдоль единичного вектора. Проекция ускорения на бинормальную линию вдоль единичного вектора B равна нулю. Таким образом, точечное ускорение находится на контактной поверхности дорожки.

Реальная природа принципа виртуальной скорости заключается в том, что этот принцип является, так сказать, общей формулой, решающей задачу статики, и поэтому он становится альтернативой другим принципам. Людмила Фирмаль

Эта плоскость имеет касательные и главные нормальные единичные векторы. Учитывая ортогональность а и а (рис. 17), согласно уравнению (18) lg «. | a, | / a, (20) Нормальная составляющая ускорения а всегда направлена внутрь вогнутой поверхности орбиты. Касательная составляющая a с 5> 0 направлена в положительную сторону касательной, то есть в направлении единичного вектора m, а когда s 0 и j ‘> 0 вектор скорости и тангенциальная составляющая ускорения направлены в одну сторону вдоль точки. Движение точки ускоряется в положительном направлении касательной к траектории.

Если s 0 и 5 0, происходит медленное движение точки в отрицательном направлении, касательном к траектории точки. Если тангенциальное ускорение исчезнет, оно будет взято из условия AT-DV, / DT = 0.

Это условие всегда выполняется, но = | и | = const, т. Е. Когда точка движется равномерно по траектории любой формы. Касательное ускорение также исчезает, когда алгебраическая скорость v достигает предельного значения, например максимального или минимального значения. Изменение в алгебраической скорости как функция 18 часов для того, что показано на рисунке, тангенциальное ускорение равно Ноль в моменты времени r и t2. Во время вибрации маятника (рис. 19) эти моменты соответствуют прохождению через точку А. Когда маятник движется в одном направлении, алгебраическая скорость в точке A максимизируется, а когда он движется в противоположном направлении, она минимизируется. Для нормализации до нуля Ускорение продолжается от условий 4 = 2 / P = 0- Это условие выполняется при p = oo.

Другими словами, это линейное движение точек. Когда точка движется по кривой траектории, p = oo в точке перегиба, где выпуклая поверхность траектории меняется на вогнутую поверхность, и наоборот (рисунок 20). Нормальное ускорение исчезает, когда u = 0, то есть когда направление точки движется вдоль траектории. В случае маятника такой момент является моментом вылета Маятник под максимальным углом как в одном направлении, так и в другом. Эти моменты соответствуют моментам Новое в маятнике.

Любая геодезическая линия, проведенная на вытянутом эллипсоиде вращения, представляет собой helpoloform, который может быть образован эллипсом с центральным качением, закрепленным вдоль этой плоскости. Людмила Фирмаль

Случай обработки т * 0 Рис. 21 Тангенциальное ускорение и нормальное ускорение ноль и их общая формула указывают, что тангенциальное ускорение характеризует изменение величины вектора скорости и изменение направления нормали. Пример. Точка движется по дуге окружности радиуса R по закону s = R-sinωr (где ω = const). Начните считать расстояние и время. Направление положительного расстояния также показано на рисунке. 21. Определите скорость Ускорение в момент времени I и значения в точке О и точке орбиты М скорость исчезает.

Решения. Проекция скорости и ускорения на естественную ось определяется уравнениями (16) и (19). У нас есть: i /, = i = R t; a, = s = -Яш2sinш /; a „-vi / p-R2 l / R = Ra> cosa> f = 0, то есть t1 = π Мы смотрим на этот пример, где скорость исчезает при / (2a>): /, = i / (2y), то есть в момент изменения направления точки, , = -H2, a, = 0. «Получить выражения a и a, r = 0, 1>, = Jash. A, = 0. a„ = R

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник