Модель что если это способ усреднения точек ряда
5.3. Методы выделения систематических составляющих ряда
Процедура выделения неслучайной систематической составляющей называется сглаживанием временного ряда .
Условно методы сглаживания можно разделить на два класса: аналитические методы и алгоритмические — методы сглаживания типа скользящего среднего.
Аналитические методы основаны на приближении регулярной составляющей ряда некоторой известной с точностью до параметров функцией, для оценки которой используются методы регрессионного анализа. При этом в качестве зависимой переменной выступает значение yt, а независимой переменной является время t.
Алгоритмические методы основаны на простой идее усреднения наблюдаемых соседних значений ряда.
Отметим, что как аналитические, так и алгоритмические методы позволяют сделать выводы о систематической составляющей на основании только наблюдаемых значений анализируемого ряда без привлечения какой — либо дополнительной информации о влиянии факторов, под действием которых она возникает.
5.3.1. Полиномиальные тренды
Часто на практике, если теория не дает явного выражения для функции f(t) в модели ( 5.1 ), ее можно аппроксимировать полиномом от времени t. В простейшем случае, если ряд имеет тенденцию равномерного возрастания или убывания его значений, тренд достаточно хорошо можно описать полиномом первой степени, то есть с помощью линейной функции. С помощью полинома второй степени (параболы) можно описать тенденцию возрастания и последующего убывания значений ряда (или наоборот). С помощью полиномов более высоких степеней можно выделить систематическую циклическую составляющую (циклический тренд).
В более сложных случаях, подбирая полином соответствующей степени, мы в принципе можем получить описание любого конечного ряда с желаемой (необходимой) точностью. Отметим, что аппроксимирующий полином служит лишь заменой некоторой объективно существующей, но неизвестной функции времени и чаще всего его коэффициентам нельзя дать какой — либо разумной содержательной интерпретации.
Итак, будем предполагать, что тренд является полиномом степени p
 |
 |
где 

 |
Полиномы имеют наиболее простую структуру и удобны с точки зрения получения формально-математических результатов, однако ограничиваться только ими не следует. Так же как в регрессионных моделях, рассмотренных в предыдущих разделах, уместно выбирать любую функцию времени, которая наиболее адекватно описывает тренд. Виды различных нелинейных регрессионных зависимостей, которые могут использоваться и для описания тренда, приведены в п. 4.9 . Для их оценки может потребоваться применение нелинейного метода наименьших квадратов.
Пример 5.4. Сглаживание временного ряда для индекса Доу — Джонса
Рассмотрим временной ряд для индекса Доу — Джонса, представленный на рис. 5.1 (данные примера 5.1). Проведем сглаживание этого ряда полиномами различных степеней. Уравнения полиномов, оцененных по методу наименьших квадратов и соответствующие коэффициенты детерминации имеют вид
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
где t = -2, -1, 0, 1, 2. Критерий наименьших квадратов в этом случае имеет вид
 |
 |
Заметим, далее, что при нечетных k 
 |
Таким образом, сглаженное значение ряда равно
 |
 |
 |
 |
 |
 |
 |
 |
Из полученного соотношения мы снова видим, что веса при наблюдениях имеют симметричные значения относительно средней точки и их сумма равна единице.
Решая примеры, мы вычислили веса для некоторых конкретных значений p и m. При этом мы установили, что сумма весов равна единице и они имеют симметричные значения относительно средней точки окна. Аналогичные вычисления можно провести и для других значений p и m. При этом окажется, что свойства весов сохраняются при любых значениях p и m.
Таким образом, при применении метода скользящего среднего для сглаживания временных рядов нет необходимости каждый раз решать задачу оценивания параметров соответствующего полинома. Достаточно использовать заранее вычисленные значения весовых коэффициентов. В книге М. Кендалла и А. Стьюарта [ 19 ] соответствующие веса приведены вплоть до значений степени полинома p = 5.
Пример 5.11. Сглаживание временного ряда примера 5.3
Наиболее наглядно эффект от применения метода скользящей средней проявляется при сглаживании временного ряда примера 5.3 — объема экспорта оборудования в Китай. На рис. 5.17 изображен график аппроксимирующей кривой, полученной простым усреднением в скользящем окне из двух соседних точек. Сравнивая рис. 5.17 с рис. 5.14 — 5.16 , видим, что применение простейшего варианта метода скользящей средней дает намного лучший результат, чем сглаживание данного ряда полиномами высокого порядка. На рис. 5.18 дан график сглаживающей кривой, полученной усреднением по трем точкам в скользящем окне. Сравнивая рис. 5.17 и 5.18 видим, что увеличение количества точек в скользящем окне приводит к ухудшению аппроксимации ряда.

Рис. 5.17
Скользящее среднее, 2 точки

Рис. 5.18
Скользящее среднее, 3 точки
Сглаживание ряда в краевых точках
Для определения сглаженных значений ряда в m первых и m последних точках можно использовать слаживающие полиномы, построенные соответственно по первым 2m + 1 и последним 2m + 1 точкам временного ряда. При этом необходимо вычислять МНК — оценки всех коэффициентов полинома.
Пример 5.12. Построение кубического полинома в краевых точках
Решая уравнения ( 5.28 ) — ( 5.31 ), можно найти коэффициенты полинома
 |
здесь суммирование проводится по индексу t = -3, -2, -1, 0, 1, 2, 3. Сглаженные значения ряда в точках t = 1, 2, 3 (эти точки мы рассматриваем как последние точки анализируемого временного ряда) получаются, если вычисленные значения коэффициентов подставить в полином ( 5.27 ). Тогда получим
 |
Как видим, веса в этих формулах тоже не зависят от наблюдений и их можно вычислить заранее.
Проведите сглаживание в краевых точках с помощью полинома второго порядка.
Влияние применения процедуры выделения тренда методом скользящей средней на случайную составляющую
Предположим, что реальный процесс порождается полиномиальным трендом и случайной составляющей, и мы точно знаем порядок полинома. Тогда, казалось бы, выделяя тренд с помощью процедуры скользящего усреднения и вычитая его из наблюдаемого ряда, мы должны получить только случайные составляющие. Однако на самом деле этого не получиться, поскольку при вычислении скользящих средних по наблюдениям временного ряда мы одновременно усредняли и случайные составляющие, как бы выделяя тренд и среди них. Чтобы убедиться в этом, рассмотрим влияние процедуры усреднения с равными весами на остаточный случайный член, который мы будем полагать гомоскедастичным с дисперсией, равной 
 |
Хотя случайные величины ut некоррелированы, после усреднения величины 



5.3.3. Метод экспоненциального сглаживания
Как мы отмечали ранее, одной из основных задач анализа временных рядов является прогноз (оценка будущих значений) или экстраполяция ряда в будущее. При этом часто необходимо учитывать устаревание данных, а именно, тот факт, что для прогноза большую ценность имеют последние наблюдения ряда, нежели прошлые отдаленные наблюдения (в рассмотренном методе скользящего среднего все наблюдаемые данные были равноценны).
Метод экспоненциального сглаживания ( экспоненциального скользящего среднего, экспоненциально — взвешенного скользящего среднего ) придает больший вес последним, «новым» данным по сравнению с прошлыми, «старыми» наблюдениями.
Идея метода заключается в следующем. Сглаженное значение ряда в некоторой точке t определяется из условия минимума следующего критерия
 |
 |
 |
При достаточно малых 
При достаточно длинных прошлых отрезках ряда для вычисления экспоненциальной скользящей средней можно использовать следующую приближенную рекуррентную формулу
 |
Пример 5.13. Экспоненциальное сглаживание ряда примера 5.3
На рис. 5.19 , 5.20 изображены графики сглаживающих кривых, построенных при различных значениях параметра 

Рис. 5.19
Экспоненциальное сглаживание, альфа 0.1

Рис. 5.20
Экспоненциальное сглаживание, альфа 0.01
Пример 5.14. Экспоненциальное сглаживание ряда примера 5.2
Рис. 5.21 , где изображен график сглаживающей кривой, построенной при значении 

Рис. 5.21
Экспоненциальное сглаживание, альфа 0.1
5.3.4. Метод последовательных (переменных) разностей
До сих пор открытым оставался вопрос о выборе порядка аппроксимирующего полинома в рассмотренных в предыдущих пунктах методах сглаживания временных рядов. Для этого можно использовать метод, который основан на вычислении последовательных разностей членов наблюдаемого ряда. Идея этого метода достаточно проста. Оказывается, что если ряд в качестве неслучайной составляющей содержит постоянный член, то ряд, полученный путем вычисления разностей первого порядка 


 |
Нетрудно видеть, что
 |
то есть ряд, составленный из последовательных разностей второго порядка, содержит только случайные составляющие вида
 |
Аналогично, после простых вычислений для ряда вида
 |
 |
В общем случае, когда
 |
можно показать, что разность порядка p + 1 записывается в виде
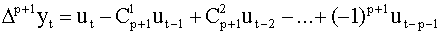 |
 |
 |
 |














 , а N может быть любым, и вычисляют значение полинома в средней точке из области его определения. Затем берут N значений ряда со сдвигом на единицу вправо, строят новый полином и вычисляют его значение в средней точке данного отрезка ряда, и так далее. Таким образом, при переходе к очередному шагу происходит как бы скольжение «окном» шириной N по всем значениям ряда. Значение N удобнее выбирать нечетным, поскольку в этом случае середина скользящего интервала (точка, в которой вычисляется значение полинома) всегда будет совпадать с очередным моментом, в котором измерено значение ряда. Ряд вычисленных значений полиномов, построенных по отрезкам ряда из скользящих окон, дает сглаженные оценки значений анализируемого ряда.
, а N может быть любым, и вычисляют значение полинома в средней точке из области его определения. Затем берут N значений ряда со сдвигом на единицу вправо, строят новый полином и вычисляют его значение в средней точке данного отрезка ряда, и так далее. Таким образом, при переходе к очередному шагу происходит как бы скольжение «окном» шириной N по всем значениям ряда. Значение N удобнее выбирать нечетным, поскольку в этом случае середина скользящего интервала (точка, в которой вычисляется значение полинома) всегда будет совпадать с очередным моментом, в котором измерено значение ряда. Ряд вычисленных значений полиномов, построенных по отрезкам ряда из скользящих окон, дает сглаженные оценки значений анализируемого ряда. зависят только от m, в уравнении ( 5.18 ) все коэффициенты cj, j=1,2,…,2m+1, зависят только от m и p и не зависят от наблюдений yt. Сглаженное значение ряда в точке t = 0 очевидно, равно
зависят только от m, в уравнении ( 5.18 ) все коэффициенты cj, j=1,2,…,2m+1, зависят только от m и p и не зависят от наблюдений yt. Сглаженное значение ряда в точке t = 0 очевидно, равно  . Следовательно, сглаженное значение ряда в точке t = 0 равно взвешенному среднему (с весами cj) его наблюдаемых значений в 2m+1 точках.
. Следовательно, сглаженное значение ряда в точке t = 0 равно взвешенному среднему (с весами cj) его наблюдаемых значений в 2m+1 точках. , из первого уравнения системы ( 5.21 ), ( 5.22 ) получим
, из первого уравнения системы ( 5.21 ), ( 5.22 ) получим означает порядковый номер наблюдения внутри окна, индексы t и
означает порядковый номер наблюдения внутри окна, индексы t и  , так что f(0)=f(m + 1). Формула скользящей средней первого порядка ( 5.23 ) не зависит от местоположения окна. Обобщая, для любого произвольного значения t, расположенного на расстоянии не менее, чем на m точек от левого и m точек от правого концов анализируемого ряда, мы можем записать
, так что f(0)=f(m + 1). Формула скользящей средней первого порядка ( 5.23 ) не зависит от местоположения окна. Обобщая, для любого произвольного значения t, расположенного на расстоянии не менее, чем на m точек от левого и m точек от правого концов анализируемого ряда, мы можем записать . Критерий ( 5.32 ) имеет смысл взвешенной суммы квадратов остатков, причем веса
. Критерий ( 5.32 ) имеет смысл взвешенной суммы квадратов остатков, причем веса  экспоненциально уменьшаются с ростом k по мере устаревания наблюдений. Приравнивая производную
экспоненциально уменьшаются с ростом k по мере устаревания наблюдений. Приравнивая производную  к нулю и решая получившееся уравнение относительно f, получим
к нулю и решая получившееся уравнение относительно f, получим — число сочетаний из k элементов по j, t=p+2, p+3,…,n. Заметим, что при взятии очередной последовательной разности исходный ряд укорачивается на единицу, так что ряд, составленный из разностей p + 1 порядка короче исходного ряда на p + 1 член. Кроме того, коэффициенты в записи ( 5.34 ) не зависят от наблюдений и легко вычисляются. Математическое ожидание и дисперсия ряда, составленного из разностей вида ( 5.34 ), равны
— число сочетаний из k элементов по j, t=p+2, p+3,…,n. Заметим, что при взятии очередной последовательной разности исходный ряд укорачивается на единицу, так что ряд, составленный из разностей p + 1 порядка короче исходного ряда на p + 1 член. Кроме того, коэффициенты в записи ( 5.34 ) не зависят от наблюдений и легко вычисляются. Математическое ожидание и дисперсия ряда, составленного из разностей вида ( 5.34 ), равны


