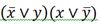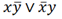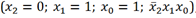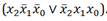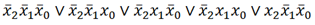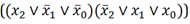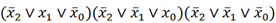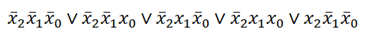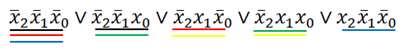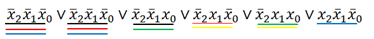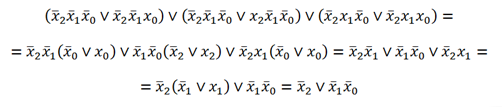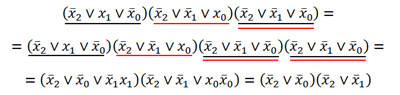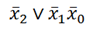Минимальная ДНФ булевой функции
На этой странице вы найдете готовые примеры по булевой алгебре , связанные с минимизацией нормальных формул булевой функции (обычно это задания вроде «найти минимальную ДНФ. «). Помимо минимальной ДНФ, в процессе решения могут быть найдены тупиковые и сокращенные ДНФ, ядерные импликанты (и ядро функции), функция Патрика и т.п.
Основные методы получения минимальной ДНФ функции это: равносильные преобразования, метод карт Карно, метод Квайна (или Квайна-МакКласки), преобразования по булевому кубу. Все они разобраны ниже. В некоторых задачах также построены релейно-контактные или функциональные схемы.
Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.
Другие примеры решений о булевых функциях:
Задачи и решения о минимизации ДНФ булевых функций
Задача 1. Применяя равносильные преобразования привести булеву функцию $f=(\bar x \to \bar y)\to (yz \to \bar xz)$ к минимальной ДНФ.
Задача 2. Для заданной логической функции: $$F= \overline <(\bar A \vee B\cdot \bar C)>\cdot \overline<( \overline <(B \downarrow C)>\cdot D> $$ — найти дизъюнктивную нормальную форму;
— составить таблицу истинности и построить диаграмму Карно;
— получить минимальную дизъюнктивную нормальную форму;
— от минимальной дизъюнктивной нормальной формы перейти к конъюнктивной нормальной форме.
Задача 3. Для функции $f(x_1,x_2,x_3,x_4)$, заданной списком номеров наборов из $Nf$ методом Квайна найти сокращенную и минимальные ДНФ.
Список номеров: 0,1,2,3,6,7,8,9,11,15.
Задача 4. С помощью карт Карно найдите сокращенную, все тупиковые и минимальные ДНФ или КНФ булевой функции f(x1,x2,x3,x4), заданной вектором своих значений.
(1100 0101 0011 0011)
Задача 5. Найти минимальные КНФ булевых функций, зависящих от аргументов $A, B, C, D$. В квадратных скобках указаны неопределенные состояния
$$f = ( 1, 2, 5, 6, 14), [4, 9, 11, 12, 15].$$
Задача 6. Найти минимальные ДНФ и КНФ булевых функций, зависящих от аргументов $A, B, C, D$
$$f = (1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14, 15).$$
Задача 7. Для булевой функции $f(x, y, z)$ найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему.
$$f(x,y,z)=(\bar x \vee \bar y)\wedge (\bar y \vee \bar z) \to (\bar x \vee \bar z)$$
Задача 8. Переключательная функция от трех аргументов задана номером в десятичной системе счисления. Получить номер ПФ в двоичном, восьмеричном и шестнадцатеричном кодах, таблицу истинности, определить СДНФ, СКНФ, символическую форму функции с восьмеричной нумерацией наборов. Минимизировать функцию по кубу соседних чисел и карте Карно. Определить свойства функции. Реализовать функцию переключательной схемой на функциональных элементах в базисах а) И, ИЛИ, НЕ, б) И-НЕ, в) ИЛИ-НЕ.
Задача 9. Для булевой функции f, заданной в таблице 1:
а) найти сокращённую ДНФ;
б) найти ядро функции;
в) получить все тупиковые ДНФ и указать, какие из них являются минимальными;
г) на картах Карно указать ядро и покрытия, соответствующие минимальным ДНФ.
Задача 10. Двумя способами: с помощью карты Карно и методом Квайна найти сокращенную, ядровую и все минимальные дизъюнктивные нормальные формы булевой функции $f$, заданной вектором значений 0101101001001110. Построить минимальную функциональную (над системой $\<\vee, \wedge, \neg\>$ ) и минимальную контактную схемы для функции $f$.
Решение задач о минимальной ДНФ на заказ
Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ о минимизации булевых функций. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 150 рублей , оформление производится в Word, срок от 2 дней.
Сокращенная и минимальная ДНФ
Сокращенная ДНФ — форма записи булевой функции, для которой 1) любые два слагаемых различаются как минимум в двух позициях, 2) ни один из конъюнктов не содержится в другом. Для булевой функции может существовать несколько сокращенных ДНФ
Минимальная ДНФ — такая сокращенная ДНФ, в которой содержится минимальное количество вхождений переменных.
Источник
Схемотехника. Минимизация логических функций
Зачем это нужно?
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.
В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.
Минимизация логических функций при помощи карт Карно
Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных: 
В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.
Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
- Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
- Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
- Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
- Область должна быть как можно больше, а кол-во областей как можно меньше;
- Области могут пересекаться;
- Возможно несколько вариантов накрытия.
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
Источник
Минимизации функций



Для начала вам надо уметь составлять СДНФ и СКНФ, потому что это, скорее всего, тоже будет в контрольной. Что это такое можно прочитать и в материалах, и в других доступных источниках. Если кратко, то СКНФ — совершенно конъюнктивная нормальная форма, а СДНФ — совершенно дизъюнктивная нормальная форма.
Совершенно конъюнктивная НФ — конъюнкция дизъюнкций, причём в каждой дизъюнкции (в каждой скобке) присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых дизъюнкций, в каждой дизъюнкции нет одинаковых слагаемых:
СКНФ:
Совершенно дизьюнктивная НФ — дизьюнкция коньюнкций , причём в каждой коньюнкции присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых коньюнкций, в каждой коньюнкции нет одинаковых слагаемых:
СДНФ:
Теперь рассмотрим пример, в котором по таблице истинности построим СДНФ и СКНФ, а затем уже перейдём к минимизации.
Для примера возьмём функцию с тремя переменными и уже разобранную на занятии.
Рассмотрим по пунктам, как составить СДНФ:
1. Записываем произведение наборов переменных 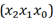
2. Берём переменную с отрицанием, если её значение равно 0
3. Между каждым произведением набора переменных ставим знак логического сложения
Теперь составим СДНФ для нашей таблицы истинности.
СДНФ:
Рассмотрим по пунктам, как составить СКНФ:
1. Записываем произведение наборов переменных 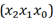
2. Берём переменную с отрицанием, если её значение равно 1 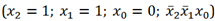
3. Между каждым произведением набора переменных ставим знак логического сложения
Составим СКНФ для таблицы истинности.
СКНФ:
Теперь перейдём к минимизации функций.
Сначала рассмотрим способ, с помощью которого мы будет упрощать СДНФ и СКНФ. Начнём с СДНФ:
Теперь ищем пары слагаемых, которые отличаются только одной переменной, то есть в одном случае она с отрицанием, в другом – без. Выделяем такие пары (тут такие пары будут выделены одинаковыми цветами) :
Но стоит заметить, что если разбить слогаемые на пары, то одно из слогаемых останется без пары. И тут мы обращаемся к аксиомам алгебры логики: 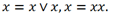
Теперь делим слогаемые на пары и выносим за скобки одинаковые переменные, после чего содержимое скобок сокращаются (как и почему это происходит, вы должны знать):

Скорее всего контрольная у нас будет по СДНФ, но к СКНФ тоже надо быть готовым. А теперь то, что точно будет в контрольной. Карты Карно – ещё один способ минимизации.
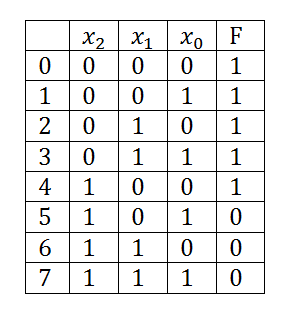
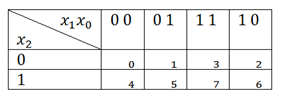
Работать будем уже с имеющейся у нас таблицей истинности. Для начала рисуем такую таблицу:
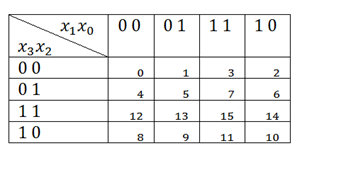
Отдельно нужно отметить нумерацию внутри таблицы. Это вам стоит запомнить.
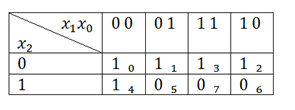
Теперь заполняем таблицу. Соответствующие клетки заполняем 1, если F=1, и оставляем пустыми либо ставим 0, если F=0:
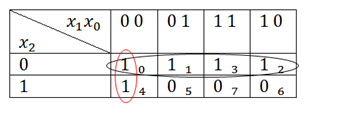
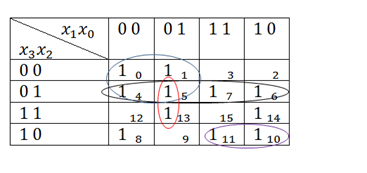
Теперь ищем группы соседних 1, которые зацикливаются. Соседними являются 1, стояие рядом друг с другом по горизонтали и по вертикали. Так же соседними являются крайние 1, то есть 1 из клетки 0 являяется соседней с 1 из клетки 2. Если трудно понять, что значит «зацикливаются», то можете запомнить, что группы единиц могут состоять из 2, 4, 8 и любому другому колличеству единиц равному 2 в степени n. А зациклиться такие группы могут только в квадрате или прямоугольнике. Так же в разные группы, при необходимости, могут попадать одни и теже 1. В конце я рассмотрю её пару отдельных случаев, а пока вернёмся к примеру. Итак, выделяем группы:
Пусть группа, выделенная чёрным, будет группой 1, а выделенная красным – группой 2. Смотрим в группах переменные, которые остаются неизменными. В группе 1 это x2, а в группе два – x1 и x0. Теперь смотрим, какие значения у этих переменных: если 0, то берём переменную с отрицание, если 1, то без. И у нас получается следующее уравнение:
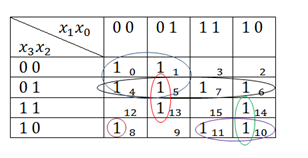
Теперь ещё немного о картах Карно. У нас в контрольных будут функции с тремя и четырьмя переменными, так что вот таблица для четырёх переменных, её нужно обязательно запомнить, особенно нумерацию.
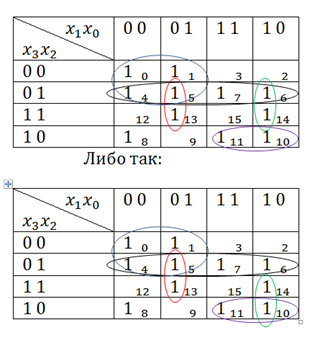
А сейчас на такой таблице рассмотрим ещё два случая, связанных с группами из 1:

Тут почти все 1 отнесенны к группам. Остальсь только 1 из клеток 14 и 8. Сначала посмотрим на 1 в клетке 14. Она соседня с 1 из клеток 6 и 10. Но, как мы уще знаем, нельзя делать группу из трёх 1. Следовательно, можно объеденить ту 1 в группу с 1 либо из клетки 6, либо из клетки 10. И то, и то будет верно. Но нельзя объединять 1 и с 1 из клетки 6, и из клетки 10. То есть либо так:
Осталась 1 в клетке 8. Тут всё просто. Если 1 не с кем зациклить, то она зацикливается сама на себе. Выглядеть это будет так:
Ну, вроде, всё. Будут вопросы, обращайтесь. Успехов всем на контрольной!
Источник