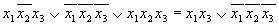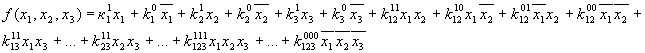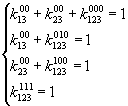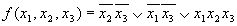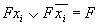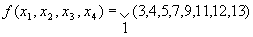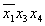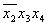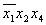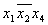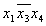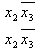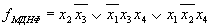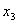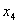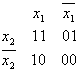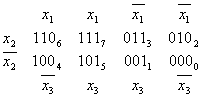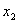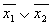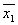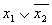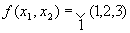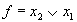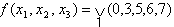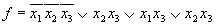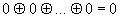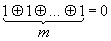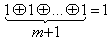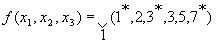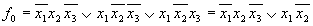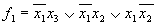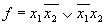Минимизировать фал аналитическим способом

Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

Аналитический метод минимизации ФАЛ

Содержание

Описание метода

Основным методом минимизации логических функций, представленных в виде СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например: X 1 ¯ X 2 X 3 X 4 ∨ X 1 ¯ X 2 X 3 ¯ X 4 = X 1 ¯ X 2 X 4 ( X 3 ∨ X 3 ¯ ) = X 1 ¯ X 2 X 4 <\displaystyle \overline X_2X_3X_4\vee \overline X_2 \overline X_4= \overline X_2X_4(X_3\vee\overline )=\overline X_2X_4>

Возможность поглощения следует из очевидных равенств:

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.

Правило склеивания

Заключается в замене логической суммы двух элементарных конъюнкций, отличающихся только знаком отрицания над одной из переменных, одной элементарной конъюнкцией, которая является общей частью рассматриваемых слагаемых, т.е. F X ∨ F X ¯ = F <\displaystyle FX \vee F \overline =F >

Правило поглощения

Дизъюнкцию двух элементарных конъюнкций, из которых одна полностью содержится в другой, можно заменить конъюнкцией, имеющей меньший ранг, например:

Источник

Схемотехника. Минимизация логических функций

Зачем это нужно?

Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.

К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.

В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.

Минимизация логических функций при помощи карт Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

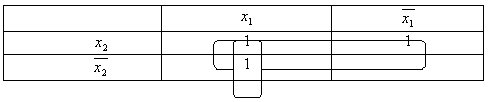
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

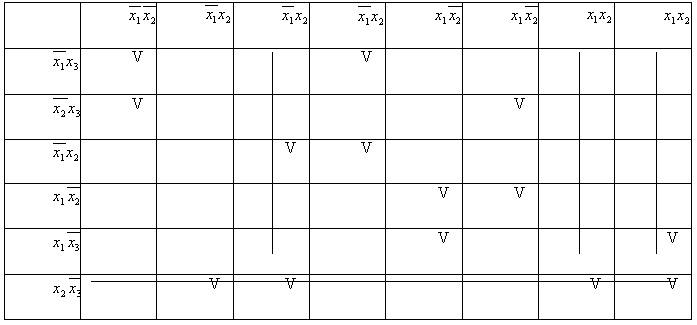
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

1. Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2 n (n целое число = 0…) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
2. Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
3. Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
4. Область должна быть как можно больше, а кол-во областей как можно меньше;
5. Области могут пересекаться;
6. Возможно несколько вариантов накрытия.

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):

Источник

Минимизация ФАЛ

Минимизация ФАЛ

Совершенно нормальные формы хотя и дают однозначные представления функции, но являются очень громоздкими. Реализация СНФ программно или схемотехнически является избыточной, что ведет к увеличению программного кода, поэтому существуют методы упрощения логической записи – минимизации.

Определение: Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.

Существуют два направления минимизации:

1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ.

2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу).

При этом следует учесть, что ни один из способов минимизации не универсален!

Существуют различные методы минимизации:

1. Метод непосредственных преобразований логических функций.(1.1)

При применении данного метода:

а) Записываются ДСНФ логических функций

б) Форма преобразуется и упрощается с использованием аксиом алгебры логики. При этом, в частности, выявляются в исходном ДСНФ так называемые соседние min-термы, в которых есть по одной не совпадающей переменной.

По отношению к соседним min-термам применяется закон склейки, значит ранг min-терма понижается на единицу.

Определение: Min-термы, образованные при склеивании называются импликантами.

Полученные после склейки импликанты по возможности склеивают до тех пор, пока склеивание становится невозможным.

Определение: Несклеивающиеся импликанты называются прослойками.

Определение: Формула, состоящая из простых импликант – тупиковая.

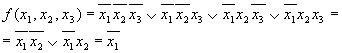
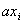
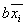
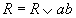
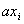
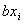
Если в процессе склейки образуется форма R, содержащая члены вида и то для нее справедливо выражение , что позволяет добавить к исходной форме R несколько членов вида пар и и после этого продолжить минимизацию.

Мы получили минимальную СНФ.

Метод неопределенных коэффициентов.(1.2)

Суть метода состоит в преобразовании ДСНФ в МДНФ.

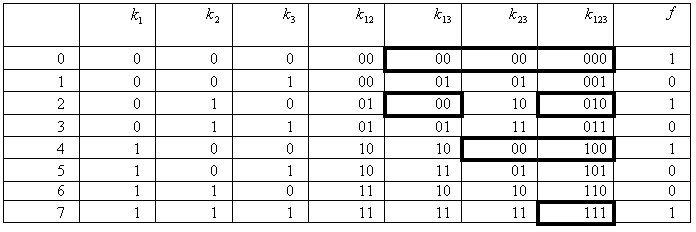
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим на примере трех переменных):

Алгоритм определения коэффициентов:

1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности.

2. Напротив каждого выражения поставить соответствующее значение функции.

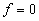
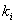
3. Выбрать строку, в которой значение функции и приравнять все к нулю.

4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках.

5. Проанализировать оставшиеся коэффициенты в единичных строках.

6. Используя правило, что дизъюнкция равна 1 если хотя бы один из 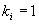, выбрать min-термы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.

7. Записать исходный вид функции.

Метод неопределенных коэффициентов применим для дизъюнктивной формы и непригоден для конъюнктивной.

Итак, получим

Суть метода сводится к тому, чтобы преобразовать ДСНФ в МДНФ. Задачи минимизации по методу Квайна состоит в попарном сравнении импликант, входящих в ДСНФ с целью выявления возможности склеивания по какой-то пременной так:

Таким образом, можно понизить ранг термов. Процедура производится до тех пор, пока не остается ни одного терма, допускающего склейки с другим. Причем склеивающиеся термы помечаются *.

Определение: Непомеченные термы называются первичными импликантами.

Полученное логическое выражение не всегда оказывается минимальным, поэтому исследуется возможность дальнейшего упрощения.

1. Составляются таблицы, в строках которых пишутся найденные первичные импликанты, а в столбцах указываются термы первичной ФАЛ.

2. Клетки этой таблицы отмечаются в том случае, если первичная импликанта входит в состав какого-нибудь первичного терма.

3. Задача упрощения сводится к нахождению такого минимального количества импликант, которые покрывают все столбцы.

Алгоритм метода Квайна (шаги):

1. Нахождение первичных импликант.

Исходные термы из ДНФ записывают в столбик и склеиваю сверху вниз. Непомеченные импликанты переходят в функции на этом шаге.

2. Расстановка меток избыточности.

Составляем таблицу, в которой строки – первичные импликанты, столбцы – исходные термы. Если некоторый min-терм содержит первичный импликант, то на пересечении строки и столбца ставим метку.

3. Нахождение существенных импликант.

Если в каком-либо столбце есть только одна метка, то первичный импликант соответствующей строки является существенным.

4. Строка, содержащая существенный импликант и соответствующие столбцы вычеркиваются.

Если в результате вычеркивания столбцов появятся строки первичных импликант, которые не содержат метки или содержат одинаковые метки в строках, то такие первичные импликанты вычеркиваются. В последнем случае оставляем одну меньшего ранга.

5. Выбор минимального покрытия.

Из таблицы, полученной на шаге 3 выбирают такую совокупность первичных импликант, которая включает метки во всех столбцах по крайней мере по одной метке в каждом. При нескольких возможных вариантах отдается предпочтение покрытию с минимальным суммарным числом элементов в импликантах, образующих покрытие.

6. Далее результат записывается в виде функции.

Термы 4го ранга

Термы 3го ранга

Термы 2го ранга

* 1

* 3

* 4

* 1

* 2

* 2

* 3

* 4

* 1

* 2

* 2

* 1

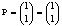
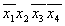
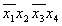
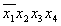
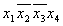
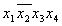
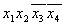
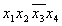
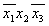
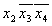
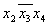
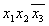
Шаг 4 пропускаем.

Выбираем те min-термы, при записи которых, МДНФ функции минимальна.

Недостаток метода Квайна – необходимость полного по парного сравнения всех min-термов на этапе нахождения первичных импликант.

Идея модификации метода Квайна – метод Квайна-Мак-Класки.(1.4)

1. Каждая конъюнкция в ДСНФ представляется своим двоичным набором.

2. Вся совокупность номеров наборов разбивается на группы в зависимости от числа единиц, имеющихся в номерах наборов (0-группа, 1-группа, 2-группа и.т.д.).

3. Сравниваются две группы, отличающиеся на одну единицу.

4. В результате сравнения в номере набора, имеющего большее число единиц на позиции, где обнаружится разница на одну единицу ставится прочерк.

5. В процессе преобразования возникают новые сочетания (n-группы).

6. Процесс преобразования длится до тех пор, пока возможна операция склеивания.

7. Элементы преобразованных групп являются первичными импликантами, которые вместе с номерами исходных наборов образуют таблицы разметок.

8. В остальном эти методы совпадают с единственным уточнением – если в результате таблицы разметок ни одна из строк не покрывает единицу столбца, то надо выбрать номер столбца набора из предыдущей группы преобразований.

Определение: n-группа – это такой набор аргументов функции, что число всех аргументов равных единице равно n, причем значении функции равно 1.

Составим таблицу истинности:

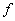
1-Группа: 0001, 0010, 0100, 1000

2-Группа: 0011, 0101, 0110, 1001

Теперь сравним группы с номерами n и n+1:

0-Группа: 000-, 00-0, 0-00, -000

1-Группа: 00-1, 0-01, -001, 001-, 0-10, 010-,01-0, 100-

2-Группа: 0-11, -011, 01-1, 011-, 10-1

3-Группа: -111, 1-11

Еще раз сравним (при этом прочерки должны быть на одинаковых позициях):

0-Группа: 00—, 0-0-, -00-

1-Группа: 0—1, -0-1, 0-1-, 01—

И еще раз сравним:

Запишем таблицу исходных min-термов, где функция равна 1:

Выделим минимальное число групп, покрывающих

Для проверки составим таблицу истинности

Метод минимизирующих карт (для ДСНФ и КСНФ).(1.5)

Одним из способов графического представления булевых функций от небольшого числа переменных являются карты Карно. Их разновидность – карты Вейча, которые строятся как развертки кубов на плоскости, при этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба.

Для ДСНФ единицы ставятся в клетке, соответствующей номеру набора, на котором значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот.

Диаграмма для двух логических переменных (для ДСНФ):

Для трех переменных:

Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие на границе карты.

При числе переменных 5 и больше отобразить графически функцию в виде единой плоской карты невозможно. Тогда строят комбинированные карты, состоящие из совокупности более простых карт. Процедура минимизации заключается тогда в том, что сначала находится минимальная форма 4-х мерных кубов (карт), а затем, расширяя понятие соседних клеток, отыскивают min-термы для совокупности карт. Причем соседними клетками являются клетки, совпадающие при совмещении карт поворотом вокруг общего ребра.

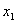
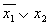
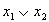
Пример: Минимизировать ФАЛ от двух переменных:

Минимизировать функцию:

Минимизация логических функций, заданных в базисе .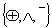

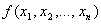
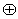
Метод неопределенных коэфициентов применим для минимизации функций, заданных в различных базисах. Пусть функция является ПСНФ, операция имеет особенности, отличающие ее от операции дизъюнкции.

1)

2)

3)

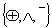
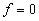
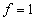
Минимизация при этом усложняется, так как ее основными критериями являются минимальные ранги каждого терма и их минимальное количество, при этом в ходе минимизации в базисе нецелесообразно приравнивать к нулю все коэффициенты на наборах где , т.к. в наборах, где функция могут остаться термы высокого ранга. Поэтому особой разницы между выбором нулевого или единичного значения функции нет.

Количество коэффициентов, остающихся в нулевых строках должно быть четным, а в единичных – нечетным. Лучше всего рассматривать единичные строки и оставлять те коэффициенты минимального ранга, которые чаще всего повторяются в этих строках. В общем случае для получения минимальной формы выполняют следующие действия:

1) Подсчитывают, сколько раз в единичных строках встречаются термы первого ранга и оставляют из них те, которые встречаются максимальное число раз.

2) Находят нулевые строки, в которых встречаются оставленные в первом шаге термы и их не обнуляют.

3) Рассматривая нулевую строку, в которой остался одни единичные термы и находят в ней еще единичный терм, встречающийся максимальное число раз в единичных строках, в которых еще не было оставлено ни одного терма и.т.д.

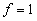
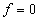
Метод Квайна-Мак-Класки может быть применим при минимизации этого базиса, при этом кроме эффективных значений функции, где включаются некоторые min-термы, где . Метод Квайна-Мак-Класки применим для минимизации базисов стрелки пирса и штриха Шеффера.

Не полностью определенные ФАЛ (1.6)

Определение: не полностью определенные ФАЛ от n переменных называется функции, заданные на множестве наборов меньше чем .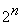

Если количество неопределенных наборов равно m то путем различных доопределений можно получить 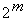различных функций.

Пример: доопределить функцию

Где символ * означает «может быть».

1)

2)

Если доопределять *=0 или *=1 то получим минимальный вариант:

3)

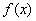
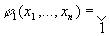
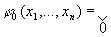
Пример показывает, что доопределение функции существенно влияет на конечный результат минимизации. При доопределении можно руководствоваться правилом: МДНФ не полностью определенных функций получается как дизъюнкция наиболее коротких по числу букв импликант функции на всех наборах и функциях, которые в совокупности покрывают все импликативные СНФ, и на всех наборах, где функция не определена.

Пример: найти минимальную форму для

Источник