Метрические задачи способы решения

Метрические задачи

В § 6 гл. I отмечалось, что при параллельном, в частности ортогональном, проецировании геометрические фигуры, произвольно расположенные по отношению к плоскостям проекций, проецируются на эти плоскости с искажением их метрических характеристик (характеристик, которые могут быть получены путем измерения линейных и угловых величин). Для того чтобы иметь возможность по метрически искаженным проекциям судить о размерах и форме оригинала, необходимо знать способы решения задач по определению неискаженных линейных и угловых величин.

Метрическими называются задачи, решение которых связано с нахождением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Все многообразие метрических задач, в конечном счете, сводится к двум видам: А — задачам на определение расстояния между двумя точками; Б — задачам на нахождение величины угла между двумя пересекающимися прямыми.

К метрическим относятся также задачи на построение отрезка и угла с наперед заданным значением соответственно линейной и градусной (радианной) величины.

Несмотря на то, что чисто метрические задачи встречаются редко, целесообразно выделйть их в самостоятельную группу, включив в нее и те задачи, в которых на промежуточных этапах решения приходится выяснять позиционные отношения между геометрическими фигурами.

В основе алгоритма решения любой метрической задачи лежит инвариантное свойство ортогонального проецирования, заключающееся в том, что любая фигура, принадлежащая плоскости, параллельной плоскости проекции, проецируется на эту плоскость в конгруентную фигуру, т. е. (Ф ⊂ β) ∧ (β || π₁) ⇒ Ф’ ≅ Ф.

Рассмотрим возможные пути решения задач на определение метрических характеристик геометрических фигур.

А. Определение расстояний.

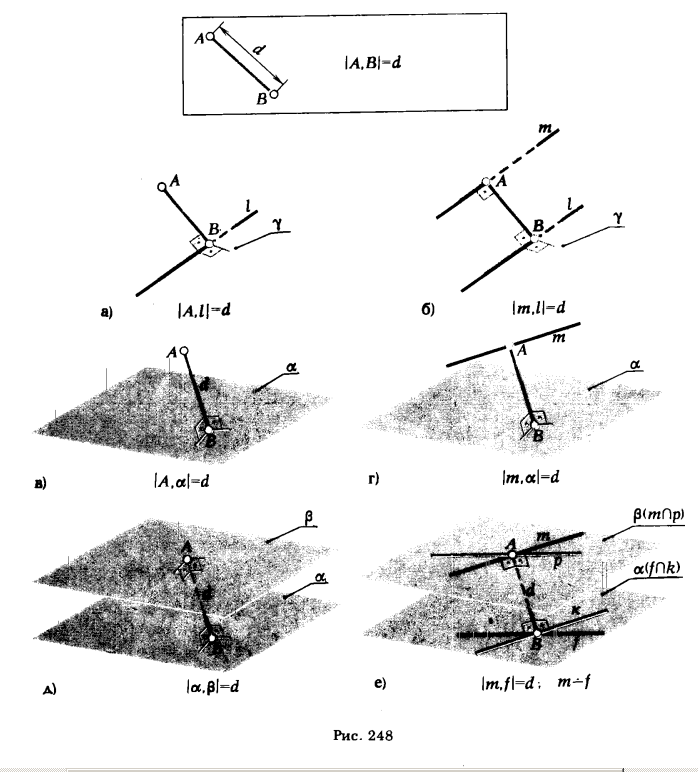
Решение задач на определение расстояния между точкой и прямой, двумя параллельными прямыми, точкой и плоскостью, прямой и плоскостью, двумя плоскостями, скрещивающимися прямыми, в конечном счете, сводится к нахождению расстояния между двумя точками.

Чертежи на рис. 248 подтверждают это утверждение. Из этих чертежей видно также, что, прежде чем приступить к решению задачи на определение расстояния между точкой и прямой или двумя параллельными прямыми (рис. 248,а и б), необходимо провести плоскость γ, перпендикулярную к прямой l, или опустить перпендикуляр из точки А (A ∈ m или A ∈ β) на плоскость α (рис. 248, в, г, д, е). Поэтому, прежде чем решать задачи на определение расстояний, выясним характер и последо-

вательность графических построений, которые должны быть выполнены для построения на эпюре взаимно перпендикулярных прямых, прямой и плоскости, плоскостей.

Источник

Метрические задачи

Содержание:

Метрическими называются задачи, решение которых связано с определением характеристик геометрических фигур, определяемых (измеряемых) линейными и угловыми величинами.

Расстояние от точки до прямой и плоскости

Расстояние от точки до плоскости – это длина перпендикуляра, который опущен из заданной точки. Чтобы найти расстояние между скрещивающимися прямыми, необходимо воспользоваться знаниями о нахождении расстояния от точки до плоскости, поскольку для определения расстояния между скрещивающимися прямыми необходимо на одной из прямой выбрать точку.

Расстояние от точки до прямой особого положения

Метрические задачи по проецированию точки, прямой и плоскости связаны с определением расстояний, площадей, углов. Все задачи на определение расстояния от точки до прямой и плоскости, между параллельными прямой и плоскостью и двумя плоскостями сводятся к задаче об определении расстояния между двумя точками. Задачи по определению площади плоской фигуры сводятся к нахождению натуральной величины этой фигуры. Определение угла между двумя прямыми, прямой и плоскостью, двумя плоскостями невозможно без применения способов преображения комплексного чертежа (см. п. 2.1.6, 2.3.3). Методами, описанными в разделе 1, можно определить только проекции этих углов.

Для определения расстояния от точки А до прямой l необходимо провести из данной точки перпендикуляр n до прямой, определить точку N пересечения прямых n, l и найти длину отрезка AN. Последняя является искомым расстоянием (рис. 1.51).

Расстояние от точки до прямой общего положения

Определение расстояния от точки до прямой уровня

При определении расстояния от точки до прямой l особого положения прямой угол между прямыми l проецируется в натуральную величину на одну из плоскостей проекций (см. п. 1.4.8), а натуральная величина отрезка АN определяется способом прямоугольного треугольника (см. п. 1.4.4) или вращением вокруг проецирующей оси (см. п. 2.2.2).

На рис. 1.52 обозначено расстояние от точки А до горизонтали h. На горизонтальной проекции построена проекция А1N1 искомого отрезка. С помощью линий проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN определена способом прямоугольного треугольника.

Расстояние от точки до прямой общего положения

Задача на определение расстояния от точки А до прямой l общего положения усложняется тем, что проекции прямого угла между прямой l и проведённым к ней перпендикуляром не равны 90° (см. п. 1.4.8, рис. 1.25). Для решения этой задачи применяются такие способы:

а) способ вспомогательной нормальной плоскости (рис. 1.53);

б) способ замены плоскостей проекций (см. п. 2.1.3);

в) способ вращения вокруг проецирующей оси (см. п. 2.2.3).

Способ вспомогательной нормальной плоскости

Суть способа вспомогательной нормальной плоскости

Через точку А проводится плоскость Σ общего положения, перпендикулярная прямой l (рис. 1.53 б). Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке А. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой l. Основа N перпендикуляра находится как точка пересечения прямой l с перпендикулярной её плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф (см. п. 1.5.7). Натуральная величина отрезка AN равна искомому расстоянию от точки А до прямой l общего положения.

Расстояние от точки до плоскости особого положения

Для определения расстояния от точки А до плоскости Σ необходимо провести из данной точки перпендикуляр до плоскости, определить точку N их пересечения и найти длину отрезка AN.

При определении расстояния от точки А до плоскости особого положения прямой угол между прямой и одним из следов плоскости Σ проецируется в натуральную величину на соответствующую плоскость проекций (рис. 1.54).

На рис. 1.55 определено расстояние от точки А до горизонтально-проецирующей плоскости Σ. На горизонтальной плоскости проекций через точку А1 проведена проекция перпендикуляра до горизонтального следа плоскости с основой N1. При этом перпендикуляр — горизонтальная прямая уровня. С помощью линии проекционной связи найдена фронтальная проекция A2N2. Натуральная величина отрезка AN равна длине его горизонтальной проекции А1N1.

Расстояние от точки до плоскости особого положения

– Определение расстояния от точки до горизонтально-проецирующей плоскости

Расстояния от точки до плоскости общего положения

Задача на определение расстояния от точки D до плоскости Σ общего положения определяется таким способом. Из точки D проводится прямая , перпендикулярная плоскости Σ (см. п. 1.5.9, рис. 1.47 – 1.48), и определяется точка N их пересечения (см. п. 1.5.7, рис. 1.38). Натуральная величина отрезка DN равна расстоянию от точки D до заданной плоскости (рис. 1.56).

Расстояние от точки до плоскости общего положения

Определение расстояния от точки до плоскости

На рис. 1.57 плоскость Σ задана треугольником АВС. Для построения прямой , проходящей через точку D перпендикулярно до плоскости треугольника, в последнем проводятся горизонталь h и фронталь f. Горизонтальная проекция h1 горизонтали перпендикулярна горизонтальной проекции прямой, фронтальная проекция f2 фронтали перпендикулярна . Точка N пересечения прямой с плоскостью Σ определяется методом вспомогательной секущей плоскости. В данном случае прямая заключается во фронтально- проецирующую плоскость Ω, заданную фронтальным следом Ω2,и определяется линия k пересечения плоскостей Σ, Ω. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка АN определяется способом прямоугольного треугольника.

Расстояние между параллельными плоскостями, прямой и плоскостью. Расстояние между двумя прямыми

Расстояние между параллельными плоскостями Σ и Ω равно расстоянию от любой точки D одной плоскости до другой плоскости (рис. 1.58).

Расстояние между параллельными плоскостями

Определение расстояния между параллельными плоскостями

На рис. 1.59 одна из плоскостей Σ задана прямыми a, b, пересекающимися в точке D, другая Ω – горизонтальным и фронтальным следами . Из точки D опускается перпендикуляр на плоскость Ω. При этом горизонтальная проекция перпендикулярна горизонтальному следу плоскости, фронтальная проекция перпендикулярна фронтальному следу Точка N пересечения прямой с плоскостью Ω определяется методом вспомогательной секущей плоскости. в данном случае через прямую проводится горизонтально-проецирующая плоскость Ψ, заданная горизонтальным следом Ψ1, и определяется линия k пересечения плоскостей Ω, Ψ. Искомая точка N является точкой пересечения прямых k, п. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой l и плоскостью Σ (рис. 1.60) равно расстоянию от любой точки D прямой до плоскости.

На рис. 1.61 плоскость Σ задана горизонтальным и фронтальным следами . Из любой точки D, принадлежащей прямой l, опускается перпендикуляр на плоскость Σ и определяется точка N их пересечения с помощью горизонтально-проецирующей плоскости Ψ. Длина отрезка DN определяется способом прямоугольного треугольника.

Расстояние между параллельными прямой и плоскостью

Определение расстояния между параллельными прямой и плоскостью

Расстояния между параллельными прямыми равно расстоянию DN от любой точки D одной прямой до другой прямой (рис. 1.62) и может быть определено способом вспомогательной нормальной плоскости (см. п. 1.6.1.2, рис. 1.53).

Расстояние между параллельными прямыми

Способ вспомогательной нормальной плоскости

На рис. 1.63 через точку D прямой l проводится Σ плоскость общего положения, перпендикулярная прямой Эта плоскость задаётся горизонталью h и фронталью f, пересекающимися в точке D. При этом горизонтальная проекция горизонтали h1 и фронтальная проекция фронтали f2 перпендикулярны соответствующим проекциям прямой . Основа N перпендикуляра находится как точка пересечения прямой с перпендикулярной ей плоскостью Σ с помощью фронтально-проецирующей секущей плоскости Ф. Натуральная величина отрезка DN равна искомому расстоянию между параллельными прямыми l, m.

Расстояние между скрещивающимися прямыми l, m равно наименьшему расстоянию от точек одной прямой до другой прямой (рис. 1.64) и определяется такими способами:

а) способом вспомогательной параллельной плоскости;

б) способами преобразования комплексного чертежа (см. п. 2.1.5, 2.2.5, 2.3.2).

Расстояние между скрещивающимися прямыми

Суть способа вспомогательной параллельной плоскости

Расстояние между скрещивающимися прямыми равно расстоянию от любой точки D одной прямой до параллельной ей плоскости Σ, проведенной через вторую прямую (рис. 1.65).

Способ вспомогательной параллельной плоскости

На рис. 1.66 через прямую проведена плоскость Σ общего положения, заданная двумя прямыми пересекающимися в произвольной точке А. Эта плоскость параллельна прямой l, поскольку проекции прямой параллельны соответствующим проекциям прямой l. Для построения прямой , проходящей через точку D перпендикулярно плоскости Σ, в последней проводятся горизонталь h и фронталь f. Горизонтальная проекция прямой перпендикулярна горизонтальной проекции h1 горизонтали, фронтальная проекция перпендикулярна f2. Точка N пересечения прямой с плоскостью Σ определяется методом вспомогательной секущей плоскости . В данном случае, через прямую проводится горизонтально-проецирующая плоскость Ω, заданная горизонтальным следом Ω2, и определяется линия k пересечения плоскостей Σ, Ω.

Искомая точка N — точка пересечения прямых k, . Длина отрезка DN определяется способом прямоугольного треугольника.

Определение расстояния между скрещивающимися прямыми

Угол между прямой и плоскостью, двумя плоскостями

Угол φ между прямой l и плоскостью Σ определяется как угол между прямой l и её проекцией на эту плоскость (рис. 1.67 а).

Угол между прямой и плоскостью

На рис. 1.67 б плоскость Σ задана горизонтальным и фронтальным следами Проекция прямой l на эту плоскость проходит через отрезок , один конец которого (точка K) — точка пересечения прямой l с плоскостью Σ, другой (точка ) – точка пересечения прямой с плоскостью Σ. Прямая проходит через любую точку N прямой l перпендикулярно плоскости Σ. Горизонтальная проекция перпендикулярна следу , фронтальная проекция перпендикулярна до Ортогональными проекциями на плоскости проекций П1, П2 угла φ между прямой l и плоскостью Σ являются соответствующие проекции угла . Натуральная величина угла φ определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).

Угол θ между двумя плоскостями Σ, Ω называется двухгранным углом (рис. 1.68). Он определяется как угол между перпендикулярами к линии k пересечения плоскостей (прямая принадлежит плоскости Σ, прямая плоскости Ω).

Двухгранный угол

Вышеуказанные способы определения углов между прямой и плоскостью и двумя плоскостями относятся к прямым способам, базирующимся на использовании определения углов φ, θ. Прямые способы имеют существенный недостаток – громоздкость вспомогательных построений .

С целью упрощения практической реализации задачи построения углов φ, θ и чтения комплексного чертежа применяются непрямые способы, базирующиеся на свойствах этих углов

Свойство угла между прямой и плоскостью

Угол φ между прямой l и плоскостью Σ дополняет вспомогательный угол до 90° (рис. 1.69 а):

Вспомогательный угол -это угол между прямой l и перпендикуляром проведенным из любой её точки D к плоскости Σ.

Вспомогательный угол

На рис. 1.69 б плоскость Σ задана горизонтальным и фронтальным следами . Проекции прямоq n, проведенyной через произвольную точку D прямой l перпендикулярно плоскости Σ, перпендикулярны соответствующим следам этой плоскости. Натуральная величина угла определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3, 2.4.2).Угол φ определяется по формуле (1.1).

Свойство двухгранного угла

Угол θ между двумя плоскостями Σ, Ω равен углу между прямыми проходящими через произвольную точку пространства перпендикулярно этим плоскостям (рис. 1.70 а).

Непрямой способ определения двухгранного угла

На рис. 1.70 б плоскости Σ, Ω заданы горизонтальными и фронтальными следами и соответственно. Проекции вспомогательных прямых перпендикулярны соответствующим следам плоскостей Σ, Ω. Натуральная величина угла определяется методами преобразования комплексного чертежа (см. п. 2.1.6, 2.3.3). Угол θ между плоскостями Σ, Ω равен углу между прямыми .

Метрические и позиционные задачи

Позиционными считаются задачи, решение которых позволяет полу-чить ответ о принадлежности точки или линии поверхности, а также зада—чи на определение общих элементов, принадлежащих различным геомет-рическим фигурам. Метрическими называются задачи, решение которых связано с нахо-ждением метрических характеристик геометрических фигур, определяе-мых линейными и угловыми величинами.

Длина дуги кривой линии

Задача на определение длины дуги s кривой линии является достаточно сложной. В начертательной геометрии она решается приближённо способом линейной интерполяции: дуга ОМ линии l разбивается на N участков которые условно заменяются одноимёнными отрезками прямых. Длина кривой ОМ определяется как сумма длин построенных отрезков с применением способов прямоугольного треугольника (рис. 3.74 а) или вращения вокруг проецирующих осей (рис. 3.74 б).

От количества N выбранных участков зависит точность определения длины дуги

Определение длины дуги кривой линии

Задача на определение длины кривой линии намного сложнее, чем расчёт площадей геометрических фигур и объёмов тел. В античные времена единственная удачная попытка определения длины кривой линии была предпринята для окружности.

Декарт высказывал ошибочную мысль, что «отношение между прямым и кривым неизвестно и не может быть познано человечеством»

. Первым достижением было определение длины дуги параболы Нейла в 1657 р. Позже К. Рэн и Х. Гюйгенс нашли длину дуги циклоиды. Незадолго до открытия математического анализа Дж. Грегори создал общую теорию нахождения дуги кривой линии.

Кристофер Рэн (Christopher Wren) – английский математик и архитектор, профессор математики в Оксфорде, член Королевского товарищества. Занимался вопросами кораблестроения, сопротивления жидкости, механикой вёсел и парусов и т.д.. Автор величественных архитектурных сооружений, в том числе Собора святого Павла.

Центр и радиус кривизны. Эволюта и эвольвента кривой

Кривизна любой линии l в точке М характеризуется двумя основными параметрами: центром и радиусом кривизны

Центр и радиус кривизны – центр С и радиус ρ окружности , которая является точнейшим приближением данной кривой l в окрестности её точки М (рис. 3.75 а).

Центр кривизны С находится на внутренней нормали кривой l в данной точке М. На рис. 3.75 б показан способ определения центра кривизны С плоской кривой l в точке М. В точке М и близко к ней расположенной точке N проведены касательные Центр кривизны С является точкой пересечения перпендикуляров к касательным. Радиус СМ построенной окружности с центром в точке С является радиусом ρ кривизны линии l в точке М..

Центр и радиус кривизны

Понятия центра и радиуса кривизны введены Лейбницем. Геометрическое место центров кривизны линии l для всех её точек называется эволютой (от латинского evolute – развитый). На рис. 3.76 показаны эволюты эллипса, дуги синусоиды и циклоиды. Для их построения на этих кривых выбирается совокупность точек … и проводятся касательные … и нормали , … Точки 1, 2, … пересечения последовательных пар нормалей являются точками, принадлежащими эволюте данной кривой. Например, эволюта эллипса (рис. 3.76 а) имеет форму звезды с двумя осями симметрии; эволюта половины дуги синусоиды (рис. 3.76 б) имеет две асимптоты и одну ось симметрии; эволюта ветви циклоиды (рис. 3.76 в) имеет одну ось симметрии.

Эволюты плоских кривых

Линия для которой заданная кривая l является эволютой, называется эвольвентой (от латинского evolvens – разворачивающий). Например, на рис. 3.76 а эллипс является эвольвентой фигуры в форме звезды.

Эволюты и эвольвенты широко используются в проектировании машин и механизмов. Например, зубчатые колёса (рис. 3.77) имеют профиль в форме кривой, эволюта которой является окружностью. Другими словами, такие зубчатые колеса имеют форму эвольвенты окружности.

Применение эвольвенты окружности

Для построения эвольвенты окружности (рис. 3.78) последняя делится на N равных частей (как правило, N = 12) точками , … Из этих точек проводятся отрезки …, касательные к окружности и с равномерно возрастающей длиной (от нуля до длины окружности). Эвольвента окружности проходит через точки 1, 2, …

Эвольвента окружности

Джеймс Грегори (James Gregory) – шотландский математик и астроном, член Королевского общества. Один из основателей математического анализа. Грегори является автором зеркального телескопа, метода определения расстояния от Земли до Солнца, способа числового интегрирования и разложения функций в бесконечные ряды.

Готфрид Вильгельм фон Лейбниц (Gottfried Wilhelm von Leibniz) – выдающийся немецкий философ, математик, физик, юрист, историк, дипломат, изобретатель, филолог; основатель и первый президент Берлинской академии наук, иностранный член Французской академии наук. Автор дифференциального и интегрального исчисления, учения про анализ и синтез, проектов научных исследований магнитного поля Земли. Лейбниц впервые ввёл термин «модель» в математических исследованиях и высказал мысль о возможности машинного моделирования функций человека. Лейбниц является автором механического арифмометра, прибора использования энергии ветра, чертежа подводной лодки, идеи создания паровой машины и т.д..

Эквидистанта кривой

Эквидистанта кривой (от латинского æquidistans – равноудалённый) – геометрическое место концов N отрезков одинаковой длины r, отложенных на нормалях к заданной кривой l (рис. 3.79 а).

На рис. 3.79 б построена эквидистанта кривой l. В точках … кривой l проводятся касательные … По одну сторону кривой l вдоль нормалей … откладываются отрезки, … одинаковой длины r, концы 1, 2, … которых принадлежат искомой эквидистанте.

Эквидистанта кривой

В металлообработке эквидистантой к траектории центра концевой фрезы является контур поверхности, которая получается в результате фрезерования. В системах автоматического раскроя плоских изделий (пластин, тканей и т.д.) эквидистанта является контуром, которым ограничивается припуск на обработку.

Расстояние от точки до кривой линии и поверхности

Расстояние от точки А до кривой линии — это наименьшее из всех расстояний l от этой точки до всех точек кривой

В начертательной геометрии расстояние l от точки А до кривой определяется способом конической поверхности (рис. 3.80).

Суть способа конической поверхности

Строится коническая поверхность Ф с направляющей , совпадающей с данной кривой, и вершиной А, которая совпадает с данной точкой. Среди совокупности прямолинейных образующих выбирается образующая l наименьшей длины.

На рис. 3.80 построен комплексный чертёж точки А и кривой . Строятся проекции образующих …, заданных отрезками , … Длины этих отрезков определяются способом вращения вокруг фронтально-проецирующей оси, проходящей через точку А. Натуральные величины … вращаются вокруг горизонтально-проецирующей оси, проходящей через точку А, до общего фронтального положения уровня.

Способ конической поверхности

Среди совокупности отрезков , … выбирается наименьший, длина которого равна искомому расстоянию от точки А до кривой .

Расстояние от точки А до кривой поверхности Ω является наименьшим из всех расстояний l от этой точки до всех точек поверхности Ω.

В начертательной геометрии расстояние l от точки А до кривой поверхности Ω определяется способом конических поверхностей.

Суть способа конических поверхностей.

Строятся конические поверхности … с вершиной А, которая совпадает с данной точкою, и направляющими , … совпадающими с направляющими поверхности Ω. Среди совокупности прямолинейных образующих каждой конической поверхности выбираются образующие … наименьших длин. По точкам полученных образующих …, принадлежащих поверхности Ω, строится кривая Расстояние от точки А до поверхности Ω равно расстоянию от этой точки до линии Она находится способом конической поверхности (рис. 3.80)

На рис. 3.81 построен комплексный чертёж точки А и поверхности Ω. Способом конических поверхностей (см. рис. 3.80) определяются наименьшие расстояния … от точки А до направляющих … По точкам 1, 2, … строятся проекции линии . Расстояние от точки А до кривой определяется способом конической поверхности (рис. 3.80)..

Описанные выше графические способы конических поверхностей являются приближенными и требуют громоздких построений. Точное, аналитическое определение расстояния от точки до кривой линии и поверхности является слишком сложной задачей поиска экстремума функции нескольких переменных параметров, которая может быть решена методами вариационного исчисления.

Способ конических поверхностей

Пересечение прямой линии с кривой поверхностью

Прямая линия l и кривая поверхность Ω могут иметь такие виды взаимного расположения:

а) прямая и поверхность не пересекаются (рис. 3.82 а);

б) прямая касается поверхности (см. п. 3.3, рис. 3.70 – 3.73);

в) прямая пересекает поверхность (рис. 3.82 б), в том числе перпендикулярна ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и кривой поверхности

Из п. 1.5.7 известно, что прямая пересекает поверхность первого порядка (плоскость) в одной точке. В случае поверхности второго и высших порядков прямая может пересекать поверхность в точках, количество которых не превышает порядок поверхности. Например, прямая может пересекать тор (поверхность четвертого порядка) максимум в четырёх точках (рис. 3.82 б).

Для определения точек пересечения прямой l с поверхностью Ω применяются такие способы:

а) способ вспомогательной секущей плоскости особого положения (см. п. 4.2.2.1, рис. 4.17 – 4.19);

б) способ вспомогательной секущей плоскости общего положения (см. п. 4.2.2.2, рис. 4.20 – 4.23);

в) способ замены плоскостей проекций (см. п. 4.2.2.3, рис. 4.24);

г) способ вращения вокруг проецирующей оси (см. п. 4.2.2.3, рис. 4.25 – 4.27);

д) метод последовательных приближений (см. п. 4.2.2.5);

е) способ косоугольного проецирования.

Все способы, кроме последнего, детально описаны в п. 4.1.2, 4.2.2 на примере гранных тел и поверхностей вращения.

Способ косоугольного проецирования является универсальным, то есть может быть использован для определения точек пересечения прямой l с любой кривой поверхностью.

На рис. 3.83 определена точка K пересечения прямой l с гиперболическим параболоидом Ω. Применён способ косоугольного проецирования на биссекторную плоскость Направление проецирования і совпадает с прямой l, поэтому проекция является точкой. Все точки и линии поверхности Ω также проецируются на биссекторную плоскость. Проекция точки пересечения прямой l с поверхностью Ω совпадает с проекцией Через точку проводится образующая принадлежащая поверхности . С помощью линии проекционной связи определяются проекция и проекции искомой точки K пересечения прямой l с гиперболическим параболоидом.

Определение точки пересечения прямой линии с кривой поверхностью

Пересечение кривой линии с плоскостью

Кривая линия l и плоскость Σ могут иметь такие виды взаимного расположения:

а) линия и плоскость не пересекаются (рис. 3.84 а);

б) плоскость касается лини (см. п. 3.3, рис. 3.70 – 3.73);

в) линия пересекает плоскость (рис. 3.84 б), в том числе перпендикулярна ей (см. п. 3.3, рис. 3.70 – 3.73).

Взаимное расположение прямой линии и плоскости

Кривая линия может пересекать плоскость в точках, количество которых не превышает порядок кривой. Например, эллипс (кривая второго порядка) пересекает плоскость максимум в двух точках (рис. 3.84 б).

Для определения точек пересечения линии l с плоскостью Σ применяются такие способы:

а) способ вспомогательной секущей цилиндрической поверхности (см. п. 4.2.2.4, рис. 4.29 – 4.30);

б) метод последовательных приближений (см. п. 4.2.2.5);

в) способ косоугольного проецирования.

Способ косоугольного проецирования может быть применён для определения точек пересечения плоскости Σ с любой кривой линией l.

На рис. 3.85 определены точки M, N пересечения кривой линииl с плоскостью Σ, заданной параллельными прямыми a, b, с применением способа косоугольного проецирования на биссекторную плоскость . Направление проецирования і совпадает с прямыми a, b, поэтому проекция является прямой. Все точки линии l также проецируются на биссекторную плоскость. Проекции точек пересечения линий l с плоскостью Σ принадлежат проекции . С помощью линий проекционной связи определяются горизонтальная и фронтальная проекции искомых точек M, N..

Определение точек пересечения кривой линии с плоскостью

Задачи на пересечение кривой линии с поверхностью, а также на пересечение поверхности плоскостью или другой поверхностью детально рассмотрены в разделе 4.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник