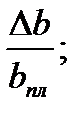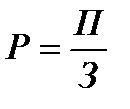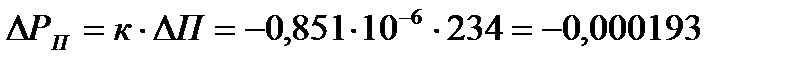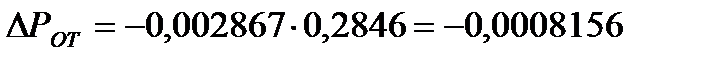Факторный анализ, его приемы: цепных подстановок, абсолютных и относительных разниц, долевого участия, интегральный.
Под факторным, анализом, понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.
В зависимости от характера исследуемых взаимосвязей различают детерминированный и стохастический факторный анализ.
Детерминированный факторный анализ исследует влияние факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда величина результативного показателя может быть представлена в виде произведения, частного или алгебраической суммы нескольких факторов.
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей.
1 . Аддитивные модели:
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей.
2. Мультипликативные модели:
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.
4.Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей:
У=(а+b)/с У=а/(b+с) У=а*b/с У=(а+b) и т.д.
Стохастический анализпредставляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной).
В детерминированном факторном анализе используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования и др.
Первые четыре способа основываются на методе элиминирования. Элиминировать — это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного!’ Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки.Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей. Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня определенного фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Рассмотрим алгоритм расчета влияния факторов для мультипликативной факторной модели типа Y = а *b * с * d.
Имеются плановые и фактические значения по каждому факторному показателю.
Определяем изменение величины результативного показателя за счет каждого фактора:
Способ абсолютных разницявляется одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях: Y = (а-b)с и Y = а(b-с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y = а *b * с * d.
Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:
Определяем изменение величины результативного показателя за счет каждого фактора:
Как правило из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Способ абсолютных разниц дает те же результаты, что и способ цепной подстановки. Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.
Способ относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа У = (а-b)с.
Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = а *b * с * d.
Изменение результативного показателя определяется следующим образом:
∆Ya = Yпл×
∆Yb = (Yпл +∆Ya) ×
∆Yc = (Yпл +∆Ya +∆Yb ) ×
Результаты расчетов те же, что и при использовании предыдущих способов.
Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.
Метод пропорционального деления и долевого участия. Применяется к кратным и смешанным моделям. Согласно методу пропорционального деления рассчитывается коэффициент пропорционального деления.


Оценка влияния каждого фактора путём умножения коэффициента пропорционального деления на изменение этого показателя.
Согласно методу долевого участия определяется объём долевого участия как удельный вес изменения исследуемого факторного показателя в общем изменении всех факторов.
В кратных моделях влияние фактора, стоящего в знаменателе, по указанным методам не всегда возможно определить объективно. Указанные приёмы, как правило, в смешанных моделях применяются в сочетании.
Рассмотрим пример использования приема пропорционального деления и долевого участия.
| Показатель | Предшествующий год | Отчетный год |
| Прибыль от реализации | ||
| Затраты на производство и сбыт продукции | ||
| в т. ч. мат. затраты | ||
| ФОТ и отчисления на соц. нужды | ||
| Амортизация ОПС | ||
| Прочие затраты |
DР=- 0,003071, DЗ=3370, DП=234
Снижение рентабельности за отчётный год было обусловлено опережающим ростом затрат над ростом прибыли.
Коэффициент долевого участия для всех видов затрат:
d 
d
d
d
Элиминирование – как способ детерминированного факторного анализа предполагает, что факторы, влияющие на результативный показатель, не зависят друг от друга. И это является существенным недостатком способа цепных подстановок и относительных и абсолютных разниц. Интегральный способ позволяет устранить этот недостаток. Этот способ используется в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида. Результаты влияния факторов не зависят от местоположения факторов в модели, что позволяет с большей точностью рассчитать их воздействие.
Рассмотрим методику расчета мультипликативных моделей:
1). А = В *С


2). на примере мультипликативной модели А = В *С* D



Для методики расчета в кратных и смешанных моделях используются следующие рабочие формулы:
1). для кратной модели

2). для смешанной модели кратно-аддитивного вида



Использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора или компьютера в Ехсе1. При этом достигается более высокая точность расчетов.
Источник
Метод цепных подстановок и абсолютных разниц



Метод цепных подстановок является одним из базовых методов экономического анализа, который применяется для анализа мультипликативных моделей. При этом каждый фактор последовательно изменяется с базисного на отчетное значение, тогда как остальные остаются без изменения.
Можно проводить расчеты в таблице. Предположим, что анализируемый показатель «А» представляет собой произведение трех факторов (Ф1, Ф2, Ф3).
Абсолютное изменение показателя известно. Необходимо определить суммы факторного влияния – насколько изменился результирующий показатель под влиянием изменения конкретного фактора. Размер факторного влияния Аф1, Аф2, Аф3 будет определяться следующим образом:
| Фактор 1 | Фактор 2 | Фактор 3 | Анализируемый показатель | Размер влияния на анализируемый показатель |
| Базисный | Базисный | Базисный | Базисный (Б) | |
| Отчетный | Базисный | Базисный | Условный 1 (У1) | Аф1 = У 1 – Б |
| Отчетный | Отчетный | Базисный | Условный 2 (У2) | Аф2 = У 2 – У 1 |
| Отчетный | Отчетный | Отчетный | Отчетный (О) | Аф3 = О – У 2 |
Общая сумма факторных отклонений дает абсолютное отклонение (изменение) показателя. Достоинством приема является то, что количество факторов не имеет значения и не влияет на методику расчета, увеличивается только количество «шагов» расчета.
Для примера представим выручку условного транспортного предприятия как произведение следующих факторов – количество машин, количество рейсов одной машины, количество пассажиров за одну поездку и стоимость проезда одного пассажира:
Данные о значении факторов в базисном и отчетном периоде представлены в таблице 7.
| Показатель | Обозначение | Базисный период | Отчетный период |
| Количество машин | М | ||
| Количество рейсов | Р | ||
| Количество пассажиров | П | ||
| Стоимость проезда | С | ||
| Выручка | В |
Абсолютное отклонение выручки составит + 180000 р.
Рассчитаем факторные отклонения. Если все факторы будут иметь базисное значение, сумма выручки составляет 1500000 р.
Затем мы будем постепенно заменять значения факторов с базисного значения на отчетное:
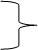
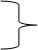
1440000 – 1800000 = — 360000.
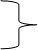
1260000 – 1440000 = — 180000.
1680000 – 1260000 = + 420000.
В отчет = 30*8*35*200 = 1680000
По итогам расчетов можно сделать вывод, что за счет увеличения количества машин предприятие получило дополнительную выручку в сумме 300000 рублей, а за счет увеличения тарифа – в сумме 420000 рублей. В то же время сказалось отрицательное влияние таких факторов, как уменьшение количества рейсов одной машины и уменьшение количества пассажиров на каждом рейсе (недополучено выручки на сумму360000 и 180000 рублей соответственно).
Прием цепных подстановок считается основным приемом факторного анализа, но имеет существенный недостаток – наличие так называемого «неразложимого остатка». Это означает, что при изменении порядка факторов в модели изменяется сумма факторных отклонений. Поэтому при составлении моделей для проведения факторного анализа существует следующее правило – сначала указываются количественные, а затем стоимостные показатели. Если необходимо обеспечить высокую точность расчетов, используются логарифмический или интегральный прием.
Метод абсолютных разниц является разновидностью приема цепных подстановок. Каждый фактор последовательно представляется в виде разницы между отчетным и базисным значениями. Остальные показатели принимаются в отчетном или базисном значении в зависимости от расположения в формуле (соответственно до анализируемого фактора или после него).
Аф1 = (Ф1о – Ф1б) * Ф2б * Ф3б;
Аф2 = Ф1о * (Ф2о – Ф2б) * Ф3б;
Аф3 = Ф1о * Ф2о * (Ф3о-Ф3б),
где Ф1б, Ф2б, Ф3б – факторы в своем базисном значении;
Ф1о, Ф2о, Ф3о – факторы в своем отчетном значении.
Вопросы для обсуждения:
1. Почему метод абсолютных разниц считается разновидностью метода цепных подстановок? Какой из предложенных приемов факторного анализа проще применять и почему?
2. Можно ли представить модель, предложенную в примере, как произведение большего количества факторов? Как произведение меньшего количества факторов?

Задачи и ситуации:
1. Рассчитать показатели рентабельности продукции и капитала по данным условного предприятия и определить, используя формулу Дюпона, влияние на изменение рентабельности активов изменения рентабельности продукции и оборачиваемости активов. Аналогичные расчеты провести по рентабельности собственного капитала.
| Показатель | Прошлый год | Отчетный год |
| Выручка | ||
| Валюта баланса | ||
| Прибыль до налогообложения | ||
| Собственный капитал |
2. Рассчитать при помощи приема абсолютных разниц:
Влияние на суммарные материальные затраты изменений в стоимости сырья и нормы расхода сырья на производство продукции.
| Показатели | Прошлый год | Отчетный год |
| Стоимость 1 кг сырья | ||
| Норма расхода, кг | ||
| Материальные затраты | ? | ? |
Определить разницу в значении факторных отклонений при изменении места расположения показателей — факторов.
3. Составить мультипликативную модель и определить факторное влияние на изменение товарооборота следующих факторов:
— средняя стоимость товара;
— количество работников торгового зала;
— количество проданных товаров на одного работника.
Источник