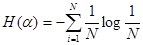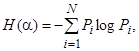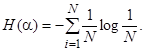ЦП Автоматизированные системы управления и промышленная безопасность
БК Автоматизированные системы управления и кибернетика
2. Меры и единицы представления, измерения и хранения информации
Количественные характеристики информации
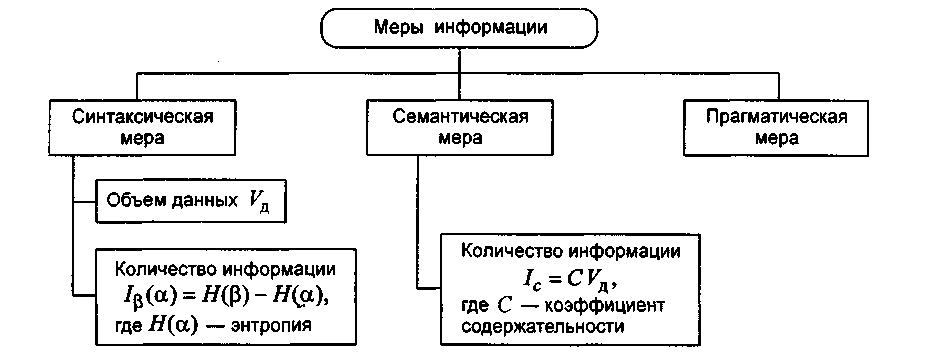
Классификация мер информации представлена на рис.1.

Рис. 1. Классификация мер информации
Синтаксическая мера информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации.
Существуют два основных подхода в определении количества информации. Исторически они возникли почти одновременно. В конце 40-х г. XX века один из основоположников кибернетики, американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к «объемному» подходу.
Объём данных (VД) понимается в техническом смысле этого слова как информационный объём сообщения или как объём памяти, необходимый для хранения сообщения без каких-либо изменений.
Информационный объём сообщения измеряется в битах и равен количеству двоичных цифр (“0” и “1”), которыми закодировано сообщение.
В компьютерной практике слово “бит” используется также как единица измерения объёма памяти. Ячейка памяти размером в 1 бит может находиться в двух состояниях (“включено” и “выключено”) и в неё может быть записана одна двоичная цифра (0 или 1). Понятно, что бит – слишком маленькая единица измерения информации, поэтому пользуются кратными ей величинами. Основной единицей измерения информации является байт. 1 байт равен 8 битам. В ячейку размером в 1 байт можно поместить 8 двоичных цифр, то есть в одном байте можно хранить 256 = 2 8 различных чисел. Для измерения ещё больших объёмов информации используются следующие величины:
1 Кбайт (один килобайт) = 2 10 байт = 1024 байта (1 kB );
1 Мбайт (один мегабайт) = 2 10 Кбайт = 1024 Кбайта (1 MB );
1 Гбайт (один гигабайт) = 2 10 Мбайт = 1024 Мбайта (1 GB );
1 Тбайт (один терабайт) = 2 10 Гбайт = 1024 Гбайта (1 TB );
1 Пбайт (один петабайт) = 2 10 Тбайт = 1024 Тбайта (1 PB );
1 Эбайт (один эксабайт) = 2 10 Пбайт = 1024 Пбайта (1 EB );
1 Збайт (один зеттабайт) = 2 10 Эбайт = 1024 Эбайта (1 ZB );
1 Йбайт (один йоттабайт) = 2 10 Збайт = 1024 Збайта (1 YB ).
Пример 1 . При двоичном кодировании текста каждая буква, знак препинания, пробел занимают 1 байт. На странице книги среднего формата примерно 50 строк, в каждой строке около 60 символов, таким образом, полностью заполненная страница имеет объём 50×60= = 3000 байт ≈3 Килобайта. Вся книга среднего формата занимает ≈0,5 Мегабайт. Один номер четырёхстраничной газеты – 150 Килобайт. Если человек говорит по 8 часов в день без перерыва, то за 70 лет он наговорит около 10 Гигабайт информации. Один чёрно-белый кадр (при 32 градациях яркости каждой точки) содержит примерно 300Кб информации, цветной кадр содержит уже около 1Мб информации. Телевизионный фильм продолжительностью 1,5часа с частотой 25 кадров в секунду — 135 Гб.
При вероятностном подходе количество информации I на синтаксическом уровне определяется через понятие энтропии системы.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), которая в то же время служит и мерой неопределенности состояния системы.
После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию Iβ(α), уменьшившую его априорную неосведомленность так, что неопределенность состояния системы после получения сообщения β стала Hβ(α).
Тогда количество информации Iβ(α) о системе, полученной в сообщении β, определится как
т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы. Если конечная неопределенность Hβ(α) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации будет определяться как Iβ(α) = H(α). Иными словами, энтропия системы Н(а) может рассматриваться как мера недостающей информации.
Энтропия системы H(α), имеющая N возможных состояний, согласно формуле Шеннона, равна:
где – вероятность того, что система находится в i-м состоянии. Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны , ее энтропия определяется соотношением:
Пример 2. Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передавать разное число состояний отображаемого объекта, что можно представить в виде соотношения
N = m n ,где N – число всевозможных отображаемых состояний;
m – основание системы счисления (разнообразие символов, применяемых в алфавите);
n – число разрядов (символов) в сообщении.
Допустим, что по каналу связи передается n-разрядное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N = m n , то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет определяться по формуле Хартли:
I = log N = n log m
Если в качестве основания логарифма принять m, то I = n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I = VД, полученных по каналу связи.
Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут соответственно бит и дит.
Семантическая мера информации
Для измерения смыслового содержания информации, т.е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение. Для этого используется понятие «тезаурус пользователя».
Тезаурус – это совокупность сведений, которыми располагает пользователь или система.
В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sp изменяется количество семантической информации Ic,воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Характер зависимости количества семантической информации, воспринимаемой потребителем, от его тезауруса показан на рис. 2.
Рис. 2. Характер зависимости количества семантической информации от его тезауруса
Рассмотрим два предельных случая, когда количество семантической информации Icравно 0:
• при пользователь не воспринимает и не понимает поступающую информацию;
• при пользователь все знает, и поступающая информация ему не нужна.
Максимальное количество семантической информации Ic потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом Sp (Sp = Sp opt), когда поступающая информация понятна пользователю и несет ему ранее не известные (отсутствующие в его тезаурусе) сведения. Следовательно, количество семантической информации в сообщении, т.е. количество новых знаний, получаемых пользователем, является величиной относительной. Одно и то же сообщение может иметь смысловое содержание для компетентного пользователя и быть бессмысленным для пользователя некомпетентного.
Относительной мерой количества семантической информации может служить коэффициент содержательности С, который определяется как отношение количества семантической информации к ее объему: .
Прагматическая мера информации (аксиологический подход)
Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цепи. Эта мера также является величиной относительной, обусловленной особенностями использования этой информации в той или иной системе.
Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.
Представим для сопоставления введённые меры информации в таб. 1.
Таб. 1. Меры информации
Источник
Мера информации рассматривающая способ представления скорость передачи надежность информации
Классификация мер
Для измерения информации вводятся два параметра: количество информации I и объем данных VД.
Эти параметры имеют разные выражения и интерпретацию в зависимости от рассматриваемой формы адекватности. Каждой форме адекватности соответствует своя мера количества информации и объема данных (рис. 2.1).
Рис. 2.1. Меры информации
Синтаксическая мера информации
Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.
Объем данных VД в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных:
• в двоичной системе счисления единица измерения — бит (bit — binary digit — двоичный разряд);
Примечание. В современных ЭВМ наряду с минимальной единицей измерения данных «бит» широко используется укрупненная единица измерения «байт», равная 8 бит.
• в десятичной системе счисления единица измерения — дат (десятичный разряд).
Пример 2.3. Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 10111011 имеет объем данных VД = 8 бит.
Сообщение в десятичной системе в виде шестиразрядного числа 275903 имеет объем данных VД = 6 дит.
Количество информации I на синтаксическом уровне невозможно определить без рассмотрения понятия неопределенности состояния системы (энтропии системы). Действительно, получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Рассмотрим это понятие.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), которая в то же время служит и мерой неопределенности состояния системы.
После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию Iβ(α), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения β) неопределенность состояния системы стала Hβ(α).
Тогда количество информации Iβ(α) о системе, полученной в сообщении β, определится как
т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность Hβ(α) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации Iβ(α) = H(α). Иными словами, энтропия системы H(α) может рассматриваться как мера недостающей информации.
Энтропия системы H(α), имеющая N возможных состояний, согласно формуле Шеннона, равна:
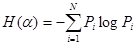
где pi — вероятность того, что система находится в i-м состоянии.
Дня случая, когда все состояния системы равновероятны, т.е. их вероятности равны Pi =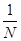
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения
где N — число всевозможных отображаемых состояний;
т — основание системы счисления (разнообразие символов, применяемых в алфавите); п — число разрядов (символов) в сообщении.
Пример 2.4. По каналу связи передается n-разрядное сообщение, использующее т различных символов. Так как количество всевозможных кодовых комбинаций будет N=m n , то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет I = log N = п log т — формула Хартли.
Источник
Меры информации



Информационный процесс
Информация динамична, она существуют непродолжительное время – столько, сколько продолжается взаимодействие данных и методов во время ее создания, потребления или преобразования. Как только взаимодействие завершается, опять в наличии данные, но уже представленные в другой форме.
Пока идет лекция студенты, используя наблюдение и прослушивание, получают информацию от преподавателя. Лекция закончилась, информация сохраняется в виде данных в коре головного мозга. На экзамене у того же преподавателя идет совершенно другой информационный процесс, студент рассказывает содержание темы, но при этом преподаватель получает совершенно другие данные и применяет к ним совершенно иные методы. В результате он получает иную информацию, которая преобразуется в данные, хранящиеся в зачетке и в ведомости на экзамен.
Подобная схема действует и в технике. Например, информационный процесс на телевидении:
Аппаратные методы: видеокамера – передающее устройство – антенна-предатчик – спутник – антенна-приемник – телевизор.
Естественные методы: зрение – головной мозг.
Преобразование данных: световой поток – заряды — электромагнитные сигналы — радиоволны – световой поток – информация – данные. На всех этапах информационного процесса идет непрерывная регистрация сигналов различной физической природы и их взаимодействие с самыми разнообразными методами.
Информационный процесс – это всегда цикл образования информации из данных и немедленного их сохранения в виде новых данных. Информация существует непродолжительное время, но информационный процесс длится столько, сколько существуют носители данных, представляющие информацию.
Понимая информацию как один из стратегических ресурсов общества, необходимо уметь его оценивать как с качественной, так и с количественной стороны. Здесь возникают проблемы из-за нематериальной природы этого ресурса и субъективного восприятия конкретной информации каждым конкретным человеком.
Для измерения информации вводятся два параметра: количество информации I и объем данных Vд. Эти параметры имеют разные выражения и интерпретацию в зависимости от рассматриваемой меры количества информации и объема данных.
Синтаксическая мера информации.
Эта мера оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту. Объем данных Vд в сообщении измеряется количеством символов (разрядов) в этом сообщении.
В различных системах счисления один разряд имеет различный вес и соответственно меняется единица измерения данных:
— в двоичной системе счисления единица измерения – бит (bit – binary digit) или более укрупненная единица байт, равная 8 бит. Сообщение, записанное двоичным кодом 10111011, имеет объем данных 8 бит или 1 байт.
— в десятичной системе счисления единица измерения – дит (десятичный разряд). Сообщение, записанное числом 275903 имеет объем данных 6 дит.
Количество информации I на синтаксическом уровне определяется с помощью понятия неопределенности состояния (энтропии) системы.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), которая в то же время служит и мерой неопределенности состояния системы. После получения некоторого сообщения β получатель приобрел некоторую дополнительную информацию Iβ(α), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения β) неопределенность состояния системы стала Hβ(α). Тогда количество информации Iβ(α) о системе, полученной в сообщении β, определится как Iβ(α) = H(α) — Hβ(α), т.е. количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность Hβ(α) обратится в нуль, то первоначальное неполное знание заменится полным знанием и количество информации Iβ(α) = H(α). Иными словами, энтропия системы H(α) может рассматриваться как мера недостающей информации.
Энтропия системы H(α), имеющая N возможных состояний, согласно формуле Шеннона, равна:

где Pi – вероятность того, что система находится в i-состоянии.
Для случая, когда все состояния системы равновероятны, т.е. их вероятности равны Pi = 1/N, ее энтропия определяется соотношением.
Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения
где N – число всевозможных отображаемых состояний;
m – основание системы счисления (разнообразие символов, применяемых в алфавите);
n – число разрядов (символов) в сообщении.
Пример. По каналу связи передается n-разрядное сообщение, использующее m различных символов. Так как количество всевозможных кодовых комбинаций будет N = m n , то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет I = log N = n log m – формула Хартли.
Если в качестве основания логарифма принять m, то I = n. В данном случае количество информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I = Vд, полученных по каналу связи. Для неравновероятностных состояний системы всегда I
Источник