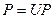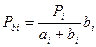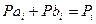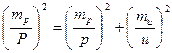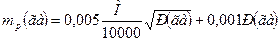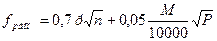Механический способ определения площади геодезия

Механический способ определения площадей.

Для механического способа определения площади фигуры любой формы применяются планиметры. Измерение производится путем обвода контура и вычисления площади по полученному отсчету. Для полярного планиметра применяются следующие формулы:

При положении полюса вне фигуры:

При положении полюса внутри фигуры:

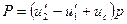
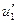
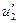
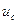
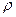
где и – отсчеты;

– постоянное число делений планиметра, круга радиусом , заключенным в площади;

р — цена деления планиметра

, R — длина отводного рычага

— деление планиметра

, R₀ — длина полюсного рычага;

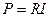
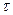
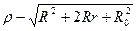
r — расстояние от оси вращения рычагов до плоскости счетного режима.

(напомнить, как с ним работать)

Запомнить: Необходимо устанавливать полюс так, чтобы при обводе фигуры угол между рычагами был не более 130 и не менее 50 , в среднем составляя 90 .

Это нам дает: 1. повышение точности определения; 2. При двух положениях полюса возможность работы даже не оттестированным прибором; 3. при обводе фигуры площадью более 1000 делений можно работать при одном положении полюса.

1. Определение площади по способу Савича.

Способ Савича применяют для определения больших площадей (землепользований) когда межевые знаки не имеют вычисленных значений координат или границы проходят по кривым линиям живых урочищ.

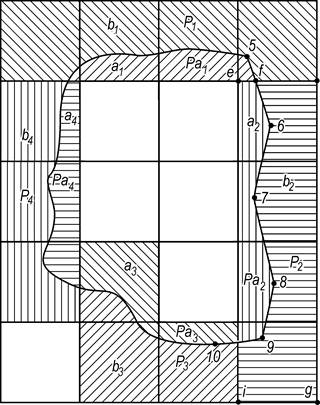
Сущность способа состоит в том, что площадь участка, заключенная в целое число квадратов координат сетки Ро определяется по их числу. Планиметром обводятся только площади секций выходящие за пределы этих квадратов (а1,а2,а3,а4) и дополнения их до целых квадратов сетки в1,в2,в3,в4 . Площади секций аі и ві обводят планиметром при 2-х положениях полюса по 2- обвода в каждом положении и выражают в делениях планиметра.

Пусть искомые площади секций в гектарах, соответствующие числам делений а1,а2,а3,а4 будут Ра1, Ра2, Ра3, Ра4. Площади целых квадратов, соответствующие числам делений аі + ві в каждой секции обозначим Р1, Р2, Р3, Р4 т.к. между площадями выраженными в га и делениях планиметра существует прямо пропорциональная зависимость можно записать:

; и т.д.

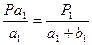
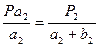
отсюда 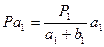и т.д.

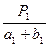
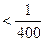
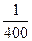
По этим формулам вычисляют площади секций, выходящие за пределы целых квадратов координатной сетки. Кроме того, следует иметь в виду, что величины и т.д. представляют значения цены деления планиметра и не большие расхождения в них меньше от величины цены деления планиметра, указывают на правильность определения величины а_і. Контроль осуществляется также путем сравнения величин а + в, выраженном площадью целых квадратов координат сетки в делениях планиметра . Относительное расхождение между значениями этих величин, соответствующих площади одного и того же числа целых квадратов координатной сетки, не должно превышать . Для контроля Р_а_i вычисляют и площади Р_ві по формуле:

Тогда

Искомая площадь будет равна Р = Ро + Ра1 +Ра2 +Ра3 + Ра4.

Если по границам некоторых секций межевые знаки имеют вычисленные значения координат, то эти площади вычисляют по координатам. Чтобы не было грубой ошибки при подсчете площади Р ее проверяют обводом всей фигуры планиметром при положении полюса внутри ее.

Допустимое расхождение 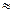0,2 % от проверяемой площади.

Достоинство способа Савича в том, что его применение механически учитывается деформация бумаги на которой составлен план или карта, уменьшается площадь обводимых фигур, чем повышается точность определения площади.

2. Точность определения площади планиметром.

Для расчета СКП определения площади Р в зависимости от СКП цены деления планиметра Р и числа делений И, полученного в результате обвода фигуры при положении полюса вне ее, воспользуемся функцией Р = иР. После всех преобразований (логарифмирования, дифференцирования и перехода к СКП) получаем:

Относительная СКП определения цены деления планиметра 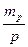при обоих положениях полюса, четырехкратным обводе трех квадратов координатной сетки близка к 1 : 1000 и влияет на погрешность определения площади независимо от размера обводимой фигуры и числа обводов.

Погрешность определения числа делений m_u получается как результат влияния погрешностей: 1). отсчетов по счетному режиму; 2). обводов; 3). механических (трения); 4). несовмещение обводного индекса с исходной точкой в начале и в конце обвода.

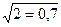
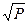
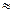
СКП отсчета составляет 0,5 деления. Для результатов одного обвода – 0,5 деления и не зависит от размера обводимой фигуры. Вторая и третья погрешности примерно одинаковы, их влияние пропорционально (площади обвода фигуры). Четвертая погрешность будет наименьшей, когда при исходном положении планиметра рычаги под углом 90° . По величине в 2 раза меньше погрешности отсчета и не зависит также от размера отводимой фигуры. Поэтому СКП при одном обводе не может быть меньше 0,7 деления планиметра и относительная СКП не может быть меньше 1 :1000. Общая СКП для одного обвода при нормальной дли обвода рычага (150 – 170 мм) можно вычислить по эмпирическим формулам:

При Р 2 на плане

см 2

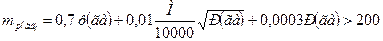
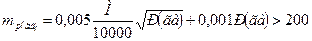
При многократных обводах все члены, кроме последнего уменьшаются пропорционально квадратному корню из числа обводов.

Например: Р + 240 га определены 2-мя обводами на плане масштаба 1 : 10000, Р 0,1 га,

По формуле (1) получаем:

га

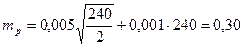
Точность определения площади по способу Савича тем выше по сравнению с непосредственным обводом всей фигуры или по частям, чем больше отношение площади целых квадратов координатной сетки к площади всей фигуры.

Если площадь целых квадратов, входящих в фигуру, составляет половину площади всей фигуры, то точность определения площади по способу Савича 3 – 4 раза больше, чем просто обводом.

Если основная площадь землепользования заключена в площадь целых квадратов координатной сетки, то точность способа Савича приближается к аналитическому.

3. Практика определения и уравнивания площадей.

1). Аналитическим (если по границам есть теодолитные хода).

2). Графическим – по графическим или фотограмметрическим координатам точек границы.

3). Планиметрии – способом Савича.

В основном площади измеряются планиметром, мелкие контуры (меньше 1 кв. см) – палетками.

При работе полярным планиметром руководствуются следующим:

1. Выпрямляют и закрепляют план. Выполняют поверки, исправления. Цену деления определяют обводом трех квадратов координатной сетки по 2 обвода при каждом положении полюса. Цена деления до 4 – 5 значащих цифр.

2. Если план склеен, надо чтобы ролик пересекал линию склейки под прямым углом (чтобы не проскальзывал по ребру бумаги).

3. Полюс устанавливать так, чтобы угол между рычагами был в среднем прим. 90° , а отклонения в обе стороны не более 60° (т.е. больше 30 и меньше 150°).

4. Исходная точка для обвода выбирается в том месте, где вращение счетного ролика оказывается самым медленным, при взаимно перпендикулярном положении рычагов.

5. Если фигуры обводятся при двух положениях полюса, полюс не перемещают, а перекладывают рычаги.

6. Площади контуров землепользования или секций обводят по 2 раза при каждом положении полюса. Площади контуров ситуации определяют двумя обводами при одном положении полюса.

7. Обводный шпиль ведут плавно, не пользоваться линейкой при обводе прямого контура.

8. Расхождение между результатами обводов не должны превышать: два деления при площади больше 200га, 3 – при площади от 200 до 2000; 4 деления – при площади больше 2000.

9. Если в ситуации много мелких контуров в несколько квадратных см, то площадь их определяют методом повторений обводки 3 – 4 раза подряд и беря отсчет перед первым и после последнего. Затем делят на число обводов

10. Площадь узких контуров определяют как площадь прямоугольников. Длину измеряют по плану, ширину на местности или по плану. Площади узких и выпрямленных контуров включают в площади соседних или вмещающих угодий с номерами этих угодий с добавлением букв (а, б, в, и т.д.).

11. Когда большое количество мелких контуров площади землепользований разбивают на секции по 50 – 100 контуров (200 – 300 кв. см на плане) площади секций увязывают в площади землепользований или трапеции, ограниченной меридианами и параллелями.

12. Допустимая невязка площадей секций в площади землепользования или в площадь трапеции определяется по формуле:

(для площади землепользования)

( для трапеции)

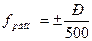
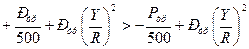
где y – ордината трапеции;

Невязку распределяют пропорционально площадям секций.

13. Дополнительную невязку в сумме площадей контуров при сравнении ее с общей площадью участка или секции вычисляют по эмпирической формуле:

где n — число контуров;

Р — общая площадь.

14. Составляется калька контуров, в которую вписывают NN контуров и их площади.

15. После вычисления площадей составляют экспликацию.

\|	следующая лекция ==>
Вопрос №4. Лингвистическая типология	\|	Нормирование точности подшипников качения.

Дата добавления: 2017-12-05 ; просмотров: 2943 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Механический способ определения площади

Механический способ заключается в измерении площадей плоских произвольных фигур на плане (карте) с помощью специальных приборов — планиметров, относящихся к семейству механико — математических интеграторов. Они бывают самых разнообразных систем: от очень простых до очень сложных. Примером простейшего планиметра (рис.4.12) может служить планиметр А. Амслера (1854 г.)

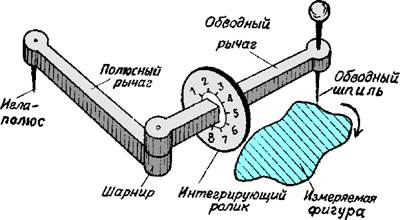
Рис.4.12. Планиметр Амслера.

В это же время нашим соотечественником Зарубиным П.А. был изобретён такой же по идее планиметр, но более сложной конструкции. Такие планиметры в настоящее время не применяют.

По конструктивным особенностям современные планиметры различают: полярные и роликовые (линейные). К полярным относят планиметры, у которых одна точка (полюс) во время обвода фигуры неподвижна, а к роликовымлинейным) — у которых все точки прибора во время обвода фигуры подвижны.

По способу фиксации результатов измерений на счетных устройствах различают механические и электронные устройства и в связи с этим появились термины: механические планиметры и электронные (цифровые) планиметры.

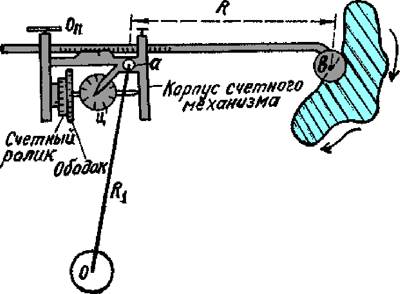
Рис. 4.13. Схема механического полярного планиметра.

Полярный планиметр (рис.4.13) состоит из трёх основных частей: двух рычагов и счетного (измерительного) ролика. Один рычаг, называемый полюсным R1, имеет на конце грузик О с иглой, которые обеспечивают неподвижность полюса в процессе работы. Другой конец этого рычага имеет штифт в виде шариковой головки для шарнирного соединения с обводным рычагом R , к которому прикреплены на одном конце обводной шпиль в, а на другом — счетный механизм с счетным роликом, называемым также интегрирующим. Для усиления сцепления счетного ролика с планом (картой) на ободок ролика наносят параллельно его оси или перпендикулярно к его плоскости мельчайшие рифельные штрихи на специальном станке. Ободок счетного ролика с рифельными штрихами является самой ответственной частью планиметра. Поэтому прикосновение потных рук к ободку счетного ролика и хранение планиметра в ненадлежащих условиях приводит к разрушению (коррозии) рифельных штрихов и планиметр оказывается непригодным к работе.

При сборке узла планиметра — счетный механизм и обводный рычаг — ось вращения счетного ролика устанавливают параллельно оси обводного рычага — линии, проходящей через точки а и в (рис.4.13) .

Результат обвода (измерения площади) фигуры определяется вращением счетного ролика, который соприкасается с поверхностью плана. Для отсчета результатов обводов на цилиндрической поверхности счетного ролика нанесены деления. Делением планиметра называют 1/1000 окружности ободка счетного ролика (примерно 0,06 мм). Поэтому отсчет по счетному ролику состоит из четырех цифр. Первую цифру (тысячи делений) отсчитывают по циферблату — относительно индекса младшая, вторую цифру (сотни) подписанную на ролике — младшая относительно нуля верньера, третью (десятки) — целое число делений на счетном ролике прошедших ноль верньера, четвертую (единицы), как число десятых долей деления ролика против нуля верньера — по совпадающим штрихам верньера и ролика.

Для работы планиметр собирается, как показано на рис. 4.14.

За прошедший период времени планиметр подвергался различным усовершенствованиям, например наряду с металлическими обводными шпилями стали применять прозрачное стекло с маленьким кружком с точкой посередине (индексом), благодаря чему контур обводимой фигуры постоянно виден, менялось количество и положение счетных устройств на обводном рычаге и др.

У механического планиметра счетный механизм может перемещаться по обводному рычагу и несколько поворачиваться относительно него для расположения рифельных штрихов параллельно оси этого рычага, т. е. линии ав (рис.4.13).

При измерениях фигуры площадью до 400 см2 на плане (карте) полюс планиметра устанавливается неподвижно вне фигуры, а шарнирное соединение в точке а обеспечивает поворот всей системы вокруг полюса О и изменение угла между рычагами. Прибор имеет три опорные перемещающиеся точки: опорный штифт у обводного шпиля, нижняя точка ободка счетного ролика и дополнительное боковое колесо 10 (рис.4.13) или сферический выступ на нижней плоскости счетного механизма.

Полярные планиметры, как правило, являются компенсационными, т.е. позволяющими выполнять измерения площадей фигур при двух положениях полюса: полюс право (ПП) и полюс лево (ПЛ). Положение полюса определяется относительно счетного механизма, если смотреть на счетный механизм со стороны обводного индекса. Если работать при полюсе право и полюсе лево, то ослабляется влияние погрешностей прибора. Измерение площади при одном положении полюса будем называть полуприемом, а при двух — полным приемом.

Полюс О на плане (карте) располагается так, чтобы при обводе шпилем в по контуру угол между рычагами R1 и R оставался в среднем близким к прямому (не менее 30º и не более 150°). На контуре выбирается начальная точка в таком месте, чтобы угол между рычагами был близким 90º, и по счетному механизму производится первый (начальный) отсчет u1. Далее фигура обводится по ходу часовой стрелки так, чтобы обводный индекс располагался над контуром. Завершается обвод возвращением обводного индекса в исходное положение, после чего по счетному механизму берется второй отсчет u2. Тогда разность n1= u2 — u1 выражает количество делений заключенное в обводимой фигуре.

Для контроля измерений производится второй аналогичный обвод, завершающийся отсчетом u3. Снова определяется разность n2= u3 — u2.

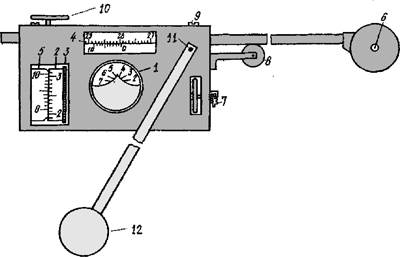
Рис. 4.14. Схема механического планиметра ПП-М: 1 — циферблат; 2 — счетный ролик; 3 — ободок счетного ролика с рифельными штрихами; 4-шкала обводного рычага с верньером; 5-верньер для счетного ролика; 6 -обводная точка (индекс); 7-исправительный винт; 8-колёсико для перемещения счетного механизма; 9-закрепительный винт; 10-опорный ролик; 11-ось шарнирного соединения рычагов; 12-полюс.

Отсчеты по счетному механизму: по циферблату -4; по шкале счетного ролика до нуля верньера -21; по штриху верньера, совпадающему со штрихом счетного ролика -7. Полный отсчет равен 4217.

Для контроля измерений производится второй аналогичный обвод, завершающийся отсчетом u3 и снова определяется разность n2= u3 — u2.

Расхождение ??n?= n1 — n2 между двумя результатами обводов контура не должно превышать трех делений для малых и средних фигур и четырех — для больших. Если ?n недопустимо, осуществляются повтор ные обводы. Значения n, не согласующиеся с другими, вычеркива ются. Из нескольких разностей n, полученных при одном положении полюса за окончательное значение площади принимается среднее.

Аналогичные измерения выполняются и при другом положении полюса. За окончательное значение площади фигуры в делениях планиметра принимается средняя разность из определений при двух положениях полюса.

Если установить цену деления планиметра р, т. е. площадь, приходящуюся на одно его наименьшее деление, то искомая площадь будет равна

к предыдущему разделу

к следующему разделу

4. Задачи, решаемые по планам (картам) при изучении местности.

4.13. Геометрическое значение цены деления планиметра и практический способ её определения.

Теоретически цена деления планиметра выражается формулой

где R — длина обводного рычага, т.е расстояние от обводного индекса до оси шарнирного соединения рычагов; τ — размер одного деления планиметра.

Обычно R≈160 мм. Величина одного деления τ зависит от диаметра счетного ролика d (обычно близок к 20 мм) и может быть определена по формуле

τ = d π /1000 = 20× 3,14 :1000 = 0,06 мм.

Геометрически цена деления планиметра представляет площадь прямоугольника с основанием, равным длине обводного рычага R, и высотой, равной одному делению планиметра τ, т.е.

р = 160мм×0,06мм ≈ 10 мм2 = 0,1 см2.

Такое значение цены деления планиметра, когда р выражается в квадратных сантиметрах или в квадратных миллиметрах на плане, называется абсолютной.

В инженерной практике пользоваться такой ценой деления нецелесообразно, т.к. величина τ очень мала и определить её с большой точностью трудно. При этом погрешность отсчета по счетному ролику на одно деление сразу же скажется на точности площадей, особенно малых размеров. Поэтому при определении площадей земельных участков на планах обычно пользуются относительной, когда цена деления выражается в квадратных метрах или гектарах на местности, т.е. с учетом масштаба плана.

Чтобы выразить относительную цену деления планиметра как площадь на местности, надо величины τ и R тоже представить на местности, а для этого их умножить на знаменатель численного масштаба плана М. Тогда относительная цена деления планиметра выразится формулой

Однако, по этой формуле цена деления планиметра тоже будет получена с большой погрешностью из-за погрешности определения τ. Поэтому относительную цену деления планиметра определяют, руководствуясь формулой (4.3). Для определения нескольких значений n фигуру, площадь которой известна, обводят при положении полюса вне фигуры. Тогда

Чтобы практически определить р, на плане выбирается удобный для обвода планиметром сравнительно большой участок с известной площадью Р. При наличии координатной сетки на плане берется два или три ее квадрата. При этом, если Р выразить в квадратных сантиметрах или миллиметрах на плане, то по формуле (4.4) получится абсолютная цена деления планиметра; если же Р выразить в квадратных метрах или гектарах на местности, то получится относительная цена деления планиметра.

Пример. Если обводились два квадрата размером 10×10 см координатной сетки на плане масштаба 1: 2 000, то их площадь Р равна (200м×400м) = 80000 м2. Среднее значение разностей при ПП получилось nср=2006, а при ПЛ — nср = 2004 делений, и среднее из двух положений полюса nср = 2005. Тогда относительная цена деления будет

р = 80000 : 2005 = 39,90 м2.

к предыдущему разделу

к следующему разделу

4. Задачи, решаемые по планам (картам) при изучении местности.

4.14. Правила работы планиметром.

Наиболее благоприятные условия для обвода площади планиметром будут в случае, когда план (карта) располагаются на горизонтальной ровной поверхности стола.

Обводный индекс следует поместить для начала обвода в конце примерной линии симметрии АВ данного контура (рис.4.15), а полюс — на перпендикуляре, восстановленном из середины М этой линии и притом так, чтобы рычаги R и R1 образовали между собой прямой угол. Тогда при прохождении обводного шпиля в верхней половине фигуры угол между рычагами все время будет тупой, а при прохождении в нижней половине — все время острый, благодаря чему погрешности будут более или менее компенсироваться.

Перед окончательной установкой полюса следует сделать примерный быстрый обвод всего контура, чтобы убедиться, что при обводе не образуется слишком острых (менее 30º) и тупых (более 150º) углов между рычагами планиметра и что ролик все время вращается свободно и не сходит с бумаги. Обвод должен производиться равномерно, не быстро, но и не слишком медленно, причем глаз должен быть расположен по направлению движения индекса (впереди или сзади него), что необходимо для удержания индекса на контуре.

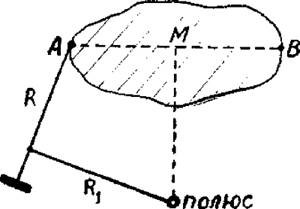
Рис. 4.15. Установка планиметра для обвода.

Рукоятку (поводок) обводного устройства следует держать свободно, без напряжения, чтобы обводный рычаг давил на план только своей тяжестью, потому что иначе под действием прилагаемой силы возможно ослабление давления счетного ролика на бумагу и даже его поднятие, т. е. проскоки в его вращении, приводящие к ошибкам в числе делений.

Полезно также между повторными обводами несколько перемещать полюс планиметра на новое место, чтобы дать возможность ролику катиться по другому пути и тем избавиться от накопления одинаковых погрешностей, зависящих от шероховатости бумаги.

к предыдущему разделу

к следующему разделу

4. Задачи, решаемые по планам (картам) при изучении местности.

4.15. Поверки планиметров.

По точности планиметр в большинстве случаев удовлетворяет требованиям землеустройства и кадастра недвижимости, тем более, что погрешность изображения площади контура на плане, вообще говоря, больше погрешности определения её планиметром. Но по производительности труда он значительно отстает от современных требований и главным образом из-за ручного обвода фигур и отсчитываний по счетному механизму. Этот способ целесообразно применять в тех случаях, когда границы участка сильно изломаны.

При получении планиметра должен производиться его осмотр, в процессе которого устанавливаются комплектность, отсутствие механических повреждений, правильность крепления отдельных частей. После этого выполняют поверки и при необходимости юстировку.

Требования к планиметру:

1) Счетный ролик должен свободно вращаться не менее 3 секунд.

При выполнении первой поверки планиметр удерживают в руках и, касаясь пальцем только пластмассового барабана счетного ролика (не ободка !), его раскручивают. Ролик должен быстро вращаться в течение нескольких секунд без ша таний. Если это условие не выполняется, то производится соответствующая регулировка положения оси счетного ролика исправительным (юстировочным ) винтом.

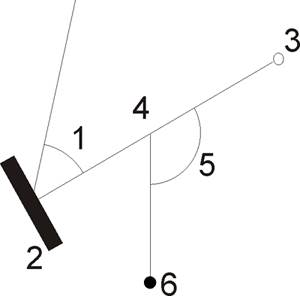
Рис.4.16. Схема планиметра при положении полюс лево (ПЛ): 1 — φ — угол из-за невыполнения основного геометрического условия; 2 — счетный ролик; 3 — обводной индекс; 4 — точка шарнирного соединения; 5 — Ө — угол между полюсным и обводным рычагами; 6 — полюс.

2) Показания счетного ролика должны быть устойчивыми при различных значениях угла Ө(рис.4.16):

— при второй позиции поверку выполнять нецелесообразно, так как не удастся выявить инструментальную погрешность. Поэтому поверку необходимо выполнять при 300

Источник