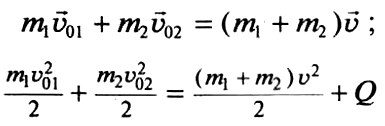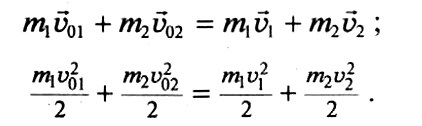Механическая энергия виды способы измерения

Механическая энергия и ее виды

п.1. Два вида механической энергии

Механическое состояние тела характеризуется его координатой в некоторой системе отсчета и скоростью.

Соответственно, энергия, связанная с изменением координаты – падением мяча, подъемом груза, сжатием газа – называется потенциальной энергией. А энергия, связанная с изменением скорости – ускорением, торможением, изменение направления движения – называется кинетической энергией тела.

Потенциальной энергией обладает груз, поднятый над поверхностью Земли. При падении, действующая на груз сила тяжести совершит работу.

Потенциальной энергией также обладает растянутая или сжатая пружина. При возвращении в недеформированное состояние, действующая на пружину сила упругости совершит работу.

Примеры тел, обладающих потенциальной энергией

Падающее тело	Сжатая пружина	Натянутая тетива лука

Кинетической энергией обладает любое движущееся тело.

Чем больше скорость тела, тем больше его кинетическая энергия.

Примеры движения тел, обладающих кинетической энергией

Автомобиль едет	Рыба плывет	Самолет летит

п.2. Единицы измерения энергии

Когда тело совершает работу, его энергия уменьшается на величину, численно равную совершенной работе. Поэтому единица измерения энергии в СИ совпадает с единицей измерения работы.

Существует также множество внесистемных единиц для измерения энергии, например: эрг (1 эрг=10 -7 Дж), калория (1 кал=4,1868 Дж), киловатт-час (1 кВт·ч=3,6·10 5 Дж), электрон-вольт (1 эВ=1,6·10 -19 Дж) и др.

п.3. Теорема о кинетической энергии

Как известно, при равноускоренном движении перемещение s можно выразить формулой $$ s=\frac <2a>$$ (см. Задача 3 §11 данного справочника).

Тогда работа силы, направление которой совпадает с направлением перемещения, равна $$ A=Fs=ma\cdot \frac<2a>=\frac<2>-\frac <2>$$

Введем величину $$ E_k=\frac <2>$$ как выражение для кинетической энергии.

Теорема о кинетической энергии носит общий характер в механике и справедлива:

1) при действии нескольких сил на тело (тогда рассматривается работа равнодействующей всех сил);

2) при действии переменной силы;

3) при действии силы, не совпадающей по направлению с перемещением;

4) для любых по своей природе сил – упругости, трения, тяжести и т.п.

п.4. Понятие консервативных сил

Потенциальная энергия определяется взаимных положением тел (например, высотой над поверхностью Земли). Понятие потенциальной энергии можно ввести только для так называемых консервативных сил.

Работа консервативной силы по перемещению тела из точки K в точку M по любому из трех путей одинакова, т.к. не зависит от пути, а зависит только от координат K и M.

Если под действием консервативной силы тело начинает движение из точки K, перемещается по замкнутой траектории и возвращается в точку K, работа по перемещению тела равна 0

Свойством консервативности обладает сила тяжести и сила упругости. Для них можно ввести понятие потенциальной энергии.

Сила трения не обладает свойством консервативности – она является диссипативной силой (см. дальше §38 данного справочника). Работа силы трения зависит от пройденного пути. Поэтому для силы трения нельзя ввести понятие потенциальной энергии.

п.5. Потенциальная энергия и работа в поле силы тяжести

Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения высоты \(h\)). Физический смысл имеет не сама потенциальная энергия, а её изменение. Если тело падает с высоты \(h_1\) на высоту \(h_2\ (h_1\gt h_2)\), сила тяжести совершает работу: $$ A=mg\Delta h=mg(h_1-h_2)=-mg(h_2-h_1)=-(E_-E_) $$ Работа силы тяжести при падении тела с высоты \(h\) на нулевой уровень \((h_1=h,\ h_2=0):\ A=mgh\). Работа положительна, т.к. направление силы тяжести (вниз) и перемещения (вниз) совпадают.

Работа силы тяжести при подъеме тела с нулевого уровня на высоту \(h\ (h_1=0,\ h_2=h):\ A=-mgh\). Работа отрицательна, т.к. направление силы тяжести (вниз) и перемещения (вверх) противоположны.

п.6. Потенциальная энергия упруго деформированного тела и работа силы упругости

Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения деформации \(x\)). Физический смысл имеет не сама потенциальная энергия, а её изменение.

Если из начального состояния с деформацией \(x_1\), пружина переходит в состояние с деформацией \(x_2\), работа силы упругости по изменению деформации: $$ A_\text<упр>=-(E_-E_)=-\left(\frac<2>-\frac<2>\right) $$ Работа по возвращению пружины в недеформированное состояние: $$ A_\text<упр>=-\frac <2>$$

п.7. Задачи

Задача 1. Как изменится кинетическая энергия автомобиля при увеличении его скорости в три раза?

Задача 2. Как изменится потенциальная энергия человека массой 80 кг при подъеме на воздушном шаре на высоту 300 м? Чему равна работа силы тяжести при подъеме?

Потенциальная энергия на поверхности Земли: \begin E_=0 \end Потенциальная энергия на высоте \(h\): $$ E_=mgh $$ Изменение потенциальной энергии: \begin \Delta E_p=E_-E_=mgh-0=mgh \end Работа силы тяжести: \begin A=-\Delta E_p=-mgh \end Получаем: \begin \Delta E_p=80\cdot 10\cdot 300=240000\ (\text<Дж>)=240\ (\text<кДж>)\\[7pt] A=-\Delta E_p=-240\ (\text<кДж>) \end Ответ: 240 кДж; -240 кДж

Задача 3. Автомобиль массой 1700 кг разгоняется из состояния покоя до скорости 108 км/ч за 6 с. Чему равна полезная мощность двигателя автомобиля, которая затрачивается на увеличение кинетической энергии? Ответ выразите в ваттах, киловаттах и лошадиных силах.

Работа силы тяги равна разности кинетических энергий автомобиля: \begin A=E_k-E_=\frac<2>-\frac<2>=\frac<2>-0=\frac <2>\end Мощность двигателя \begin N=\frac At=\frac <2t>\end Получаем \begin N=\frac<1700\cdot 30^2><2\cdot 6>=127500\ (\text<Вт>)=127,5\ (\text<кВт>)\\[6pt] 127500\ \text<Вт>\ =\frac<127500><735,5>\ \text <л.с.>\approx 173\ \text <л.с.>\end Ответ: 127500 Вт = 127,5 кВт ≈ 173 л.с.

Задача 4. Пуля массой 10 г, движущаяся со скоростью 500 м/с, пробила деревянный щит толщиной 2 см и вылетела со скоростью 300 м/с. Чему равна работа силы сопротивления движению пули в щите и модуль среднего значения силы сопротивления?

Работа силы сопротивления равна разности кинетических энергий пули: \begin A=\frac<2>-\frac<2>=\frac m2(v^2_2-v^2_1)=\frac m2(v_2-v_1)(v_2+v_1) \end С другой стороны, работа равна произведению силы на перемещение: \begin A=F_\text<ср>s\Rightarrow F_\text<ср>=\frac As \end Получаем \begin A=\frac<0,01><2>(300-500)(300+500)=-800\ (\text<Дж>) \end Работа отрицательна, т.к. тормозящая сила сопротивления направлена противоположно перемещению. В результате кинетическая энергия уменьшается. \begin F_\text<ср>=\frac<-800><0,02>=-40000\ (\text<Н>)=-40\ (\text<кН>)\\[6pt] |F_\text<ср>|=40\ \text <кН>\end Ответ: -800 Дж; 40 кН

Задача 5. Медный и алюминиевый шары одинакового объема подняли на одинаковую высоту. Для какого шара изменение потенциальной энергии больше и во сколько раз?

Потенциальная энергия тела на высоте \(h\): \begin E_p=mgh=\rho Vgh \end Потенциальная энергия на нулевом уровне: \begin E_=0 \end Изменение потенциальной энергии при подъеме: \begin \Delta E_p=E_p-E_=\rho Vgh-0=\rho Vgh \end Отношение изменений потенциальных энергий для шаров: $$ \frac<\Delta E_><\Delta E_>=\frac<\rho_1 Vgh><\rho_2 Vgh>=\frac<\rho_1> <\rho_2>$$ Изменение потенциальной энергии больше для более плотного медного шара. \begin \frac<\Delta E_><\Delta E_>=\frac<8930><2700>\approx 3,3\ (\text<раз>) \end Ответ: больше для медного шара в 3,3 раза

Задача 6. Чему равна потенциальная энергия растянутой пружины, если она растянута на 4 см и для удержания её в этом состоянии необходимо прикладывать силу 60 Н?

По закону Гука (см. §21 данного справочника) сила упругости, возникающая в растянутой пружине, равна: \(F_\text<упр>=kx\), где \(k\) — жесткость пружины, \(x\) — величина деформации.
Сила, удерживающая пружину в растянутом состоянии, должна уравновешивать силу упругости, т.е. быть равной ей по величине \(F=F_\text<упр>=kx\). По направлению эти силы противоположны: удерживающая сила растягивает пружину, сила упругости стремится вернуть её в исходное состояние.
Следовательно, жесткость пружины: \begin k=\frac Fx. \end Потенциальная энергия растянутой пружины: \begin E_p=\frac<2>=\frac Fx\cdot \frac<2>\\[6pt] E_p=\frac <2>\end Получаем: \begin E_p=\frac<60\cdot 0,04><2>=1,2\ (\text<Дж>) \end Ответ: 1,2 Дж

Задача 7*. Какую работу необходимо совершить, чтобы поднять на цепи из колодца глубиной 30 м ведро с водой? Масса цепи 8 кг, масса ведра с водой 10 кг. Размерами ведра можно пренебречь.

Установим нулевой уровень \(h=0\) на дне колодца.
При подъеме на высоту \(h\) ведро массу не меняет и приобретает потенциальную энергию \begin E_=Mgh \end Работа силы тяжести при подъеме ведра \(A’_\text<в>=-\Delta E_p=-Mgh\). Работа силы тяжести отрицательна, т.к. направление силы тяжести (вниз) противоположно перемещению (вверх).
Работа сторонних сил (силы тяги) по преодолению силы тяжести \(A_\text<в>=-A’_\text<в>=Mgh\). Работа положительна, т.к. сила тяги направлена вверх.
С цепью немного сложней, т.к. масса цепи меняется при подъеме: в начале подъема она максимальна и равна \(m=8\ \text<кг>\), в конце подъема – минимальна и равна \(m_0=0\ \text<кг>\).
При равномерном подъеме средняя масса \begin m_\text<ср>=\frac<2>=\frac m2=4\ \text<кг>. \end Тогда работа силы тяги по подъему цепи $$ A_\text<ц>=m_\text<ср>gh=\frac m2 gh. $$ Получаем: \begin A=A_\text<в>+A_\text<ц>=Mgh+\frac m2 gh\\[6pt] A=\left(M+\frac m2\right)gh \end Подставляем \begin A=\left(10+\frac 82\right)\cdot 10\cdot 30=4200\ (\text<Дж>)=4,2\ (\text<кДж>) \end Ответ: 4,2 кДж

Источник

Механическая энергия виды способы измерения

Раздел ОГЭ по физике: 1.18. Механическая энергия. Закон сохранения механической энергии. Формула для закона сохранения механической энергии в отсутствие сил трения. Превращение механической энергии при наличии силы трения.

1. Энергия тела – физическая величина, показывающая работу, которую может совершить рассматриваемое тело (за любое, в том числе неограниченное время наблюдения). Тело, совершающее положительную работу, теряет часть своей энергии. Если же положительная работа совершается над телом, энергия тела увеличивается. Для отрицательной работы – наоборот.

• Энергией называют физическую величину, которая характеризует способность тела или системы взаимодействующих тел совершить работу.
• Единица энергии в СИ 1 Джоуль (Дж).

2. Кинетической энергией называется энеpгия движущихся тел. Под движением тела следует понимать не только перемещение в пространстве, но и вращение тела. Кинетическая энергия тем больше, чем больше масса тела и скорость его движения (перемещения в пространстве и/или вращения). Кинетическая энеpгия зависит от тела, по отношению к которому измеряют скорость рассматриваемого тела.

• Кинетическая энергия Е_к тела массой m, движущегося со скоростью v, определяется по формуле Е_к =mv 2 /2

3. Потенциальной энергией называется энергия взаимодействующих тел или частей тела. Различают потенциальную энергию тел, находящихся под действием силы тяжести, силы упругости, архимедовой силы. Любая потенциальная энергия зависит от силы взаимодействия и расстояния между взаимодействующими телами (или частями тела). Потенциальная энергия отсчитывается от условного нулевого уровня.

• Потенциальной энергией обладают, например, груз, поднятый над поверхностью Земли, и сжатая пружина.
• Потенциальная энергия поднятого груза Е_п = mgh .
• Кинетическая энергия может превращаться в потенциальную, и обратно.

4. Механической энергией тела называют сумму его кинетической и потенциальной энергий. Поэтому механическая энеpгия любого тела зависит от выбора тела, по отношению к которому измеряют скорость рассматриваемого тела, а также от выбора условных нулевых уровней для всех разновидностей имеющихся у тела потенциальных энергий.

• Механическая энергия характеризует способность тела или системы тел совершить работу вследствие изменения скорости тела или взаимного положения взаимодействующих тел.

5. Внутренней энергией называется такая энергия тела, за счёт которой может совершаться механическая работа, не вызывая убыли механической энергии этого тела. Внутренняя энеpгия не зависит от механической энергии тела и зависит от строения тела и его состояния.

6. Закон сохранения и превращения энергии гласит, что энеpгия ниоткуда не возникает и никуда не исчезает; она лишь переходит из одного вида в другой или от одного тела к другому.

• Закон сохранения механической энергии: если между телами системы действуют только силы тяготения и силы упругости, то сумма кинетической и потенциальной энергии остается неизменной, то есть механическая энергия сохраняется.

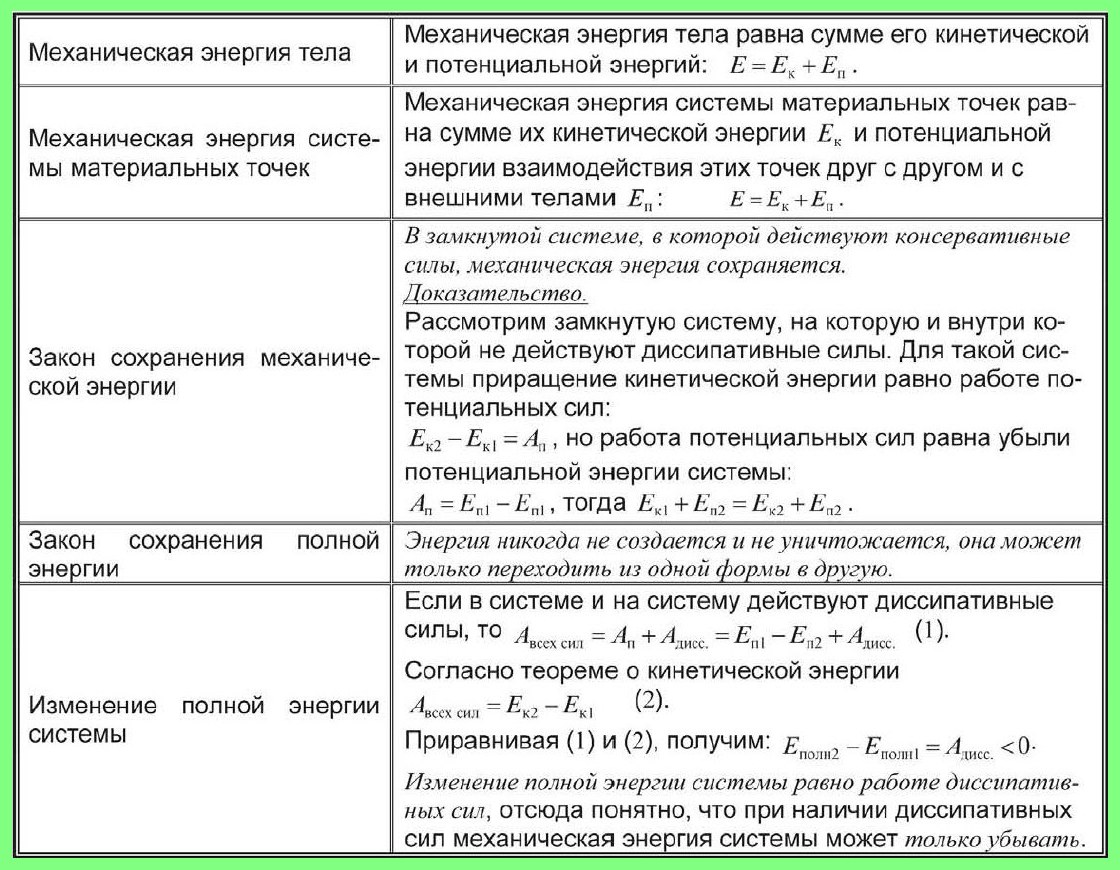
Таблица «Механическая энергия. Закон сохранения энергии».

7. Изменение механической энергии системы тел в общем случае равно сумме работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления: ΔW = А_внешн + А_диссип

Если система тел замкнута (А_внешн = 0), то ΔW = А_диссип, то есть полная механическая энергия системы тел меняется только за счёт работы внутренних диссипативных сил системы (сил трения).

Если система тел консервативна (то есть отсутствуют силы трения и сопротивления А_тр = 0), то ΔW = А_внешн, то есть полная механическая энергия системы тел меняется только за счёт работы внешних по отношению к системе сил.

8. Закон сохранения механической энергии: В замкнутой и консервативной системе тел полная механическая энергия сохраняется: ΔW = 0 или W_п1 + W_к1 = W_п2 + W_к2 . Применим законы сохранения импульса и энергии к основным моделям столкновений тел.

• Абсолютно неупругий удар (удар, при котором тела движутся после столкновения вместе, с одинаковой скоростью). Импульс системы тел сохраняется, а полная механическая энергия не сохраняется:

• Абсолютно упругий удар (удар, при котором сохраняется механическая энергия системы). Сохраняются и импульс системы тел, и полная механическая энергия:

Удар, при котором тела до соударения движутся по прямой, проходящей через их центры масс, называется центральным ударом.

Схема «Механическая энергия.
Закон сохранения энергии. Углубленный уровень«

Конспект урока по физике «Механическая энергия. Закон сохранения энергии». Выберите дальнейшие действия:

Источник