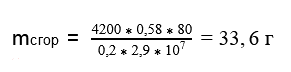- Механическая энергия и ее виды
- п.1. Два вида механической энергии
- п.2. Единицы измерения энергии
- п.3. Теорема о кинетической энергии
- п.4. Понятие консервативных сил
- п.5. Потенциальная энергия и работа в поле силы тяжести
- п.6. Потенциальная энергия упруго деформированного тела и работа силы упругости
- п.7. Задачи
- Закон сохранения механической энергии
- Энергия: что это такое
- Механическая энергия
- Кинетическая энергия
- Потенциальная энергия
- Закон сохранения энергии
- Переход механической энергии во внутреннюю
- Закон сохранения энергии в тепловых процессах
Механическая энергия и ее виды
п.1. Два вида механической энергии
Механическое состояние тела характеризуется его координатой в некоторой системе отсчета и скоростью.
Соответственно, энергия, связанная с изменением координаты – падением мяча, подъемом груза, сжатием газа – называется потенциальной энергией. А энергия, связанная с изменением скорости – ускорением, торможением, изменение направления движения – называется кинетической энергией тела.
Потенциальной энергией обладает груз, поднятый над поверхностью Земли. При падении, действующая на груз сила тяжести совершит работу.
Потенциальной энергией также обладает растянутая или сжатая пружина. При возвращении в недеформированное состояние, действующая на пружину сила упругости совершит работу.
Примеры тел, обладающих потенциальной энергией
| Падающее тело | Сжатая пружина | Натянутая тетива лука |
 |  |  |
Кинетической энергией обладает любое движущееся тело.
Чем больше скорость тела, тем больше его кинетическая энергия.
Примеры движения тел, обладающих кинетической энергией
| Автомобиль едет | Рыба плывет | Самолет летит |
 |  |  |
п.2. Единицы измерения энергии
Когда тело совершает работу, его энергия уменьшается на величину, численно равную совершенной работе. Поэтому единица измерения энергии в СИ совпадает с единицей измерения работы.
Существует также множество внесистемных единиц для измерения энергии, например: эрг (1 эрг=10 -7 Дж), калория (1 кал=4,1868 Дж), киловатт-час (1 кВт·ч=3,6·10 5 Дж), электрон-вольт (1 эВ=1,6·10 -19 Дж) и др.
п.3. Теорема о кинетической энергии
Как известно, при равноускоренном движении перемещение s можно выразить формулой $$ s=\frac
Тогда работа силы, направление которой совпадает с направлением перемещения, равна $$ A=Fs=ma\cdot \frac
Введем величину $$ E_k=\frac
Теорема о кинетической энергии носит общий характер в механике и справедлива:
1) при действии нескольких сил на тело (тогда рассматривается работа равнодействующей всех сил);
2) при действии переменной силы;
3) при действии силы, не совпадающей по направлению с перемещением;
4) для любых по своей природе сил – упругости, трения, тяжести и т.п.
п.4. Понятие консервативных сил
Потенциальная энергия определяется взаимных положением тел (например, высотой над поверхностью Земли). Понятие потенциальной энергии можно ввести только для так называемых консервативных сил.
 Работа консервативной силы по перемещению тела из точки K в точку M по любому из трех путей одинакова, т.к. не зависит от пути, а зависит только от координат K и M. |  Если под действием консервативной силы тело начинает движение из точки K, перемещается по замкнутой траектории и возвращается в точку K, работа по перемещению тела равна 0 |
Свойством консервативности обладает сила тяжести и сила упругости. Для них можно ввести понятие потенциальной энергии.
Сила трения не обладает свойством консервативности – она является диссипативной силой (см. дальше §38 данного справочника). Работа силы трения зависит от пройденного пути. Поэтому для силы трения нельзя ввести понятие потенциальной энергии.
п.5. Потенциальная энергия и работа в поле силы тяжести
 | Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения высоты \(h\)). Физический смысл имеет не сама потенциальная энергия, а её изменение. Если тело падает с высоты \(h_1\) на высоту \(h_2\ (h_1\gt h_2)\), сила тяжести совершает работу: $$ A=mg\Delta h=mg(h_1-h_2)=-mg(h_2-h_1)=-(E_ |
Работа силы тяжести при подъеме тела с нулевого уровня на высоту \(h\ (h_1=0,\ h_2=h):\ A=-mgh\). Работа отрицательна, т.к. направление силы тяжести (вниз) и перемещения (вверх) противоположны.
п.6. Потенциальная энергия упруго деформированного тела и работа силы упругости
 | Потенциальная энергия зависит от выбора системы отсчета и точки отсчета (для определения деформации \(x\)). Физический смысл имеет не сама потенциальная энергия, а её изменение. |
Если из начального состояния с деформацией \(x_1\), пружина переходит в состояние с деформацией \(x_2\), работа силы упругости по изменению деформации: $$ A_\text<упр>=-(E_ Задача 1. Как изменится кинетическая энергия автомобиля при увеличении его скорости в три раза? Задача 2. Как изменится потенциальная энергия человека массой 80 кг при подъеме на воздушном шаре на высоту 300 м? Чему равна работа силы тяжести при подъеме? Потенциальная энергия на поверхности Земли: \begin Задача 3. Автомобиль массой 1700 кг разгоняется из состояния покоя до скорости 108 км/ч за 6 с. Чему равна полезная мощность двигателя автомобиля, которая затрачивается на увеличение кинетической энергии? Ответ выразите в ваттах, киловаттах и лошадиных силах. Работа силы тяги равна разности кинетических энергий автомобиля: \begin Задача 4. Пуля массой 10 г, движущаяся со скоростью 500 м/с, пробила деревянный щит толщиной 2 см и вылетела со скоростью 300 м/с. Чему равна работа силы сопротивления движению пули в щите и модуль среднего значения силы сопротивления? Работа силы сопротивления равна разности кинетических энергий пули: \begin Задача 5. Медный и алюминиевый шары одинакового объема подняли на одинаковую высоту. Для какого шара изменение потенциальной энергии больше и во сколько раз? Потенциальная энергия тела на высоте \(h\): \begin Задача 6. Чему равна потенциальная энергия растянутой пружины, если она растянута на 4 см и для удержания её в этом состоянии необходимо прикладывать силу 60 Н? По закону Гука (см. §21 данного справочника) сила упругости, возникающая в растянутой пружине, равна: \(F_\text<упр>=kx\), где \(k\) — жесткость пружины, \(x\) — величина деформации. Задача 7*. Какую работу необходимо совершить, чтобы поднять на цепи из колодца глубиной 30 м ведро с водой? Масса цепи 8 кг, масса ведра с водой 10 кг. Размерами ведра можно пренебречь. Установим нулевой уровень \(h=0\) на дне колодца. Источник О чем эта статья: Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно. Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы. Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу. Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия. Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической. Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия. Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость. Кинетическая энергия Ек = (m*v^2)/2 Ек — кинетическая энергия [Дж] m — масса тела [кг] Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия. Задачка раз Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с. Решение: Формула кинетической энергии Ек = (m*v^2)/2 Ек = (10*2^2)/2 = 20 Дж Ответ: кинетическая энергия пёсы равна 20 Дж. Задачка два Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж Решение: Формула кинетической энергии Ек = (m*v^2)/2 Ответ: гном бежал со скоростью 2 м/с. В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия. Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия. Потенциальная энергия деформированной пружины Еп — потенциальная энергия [Дж] k — жесткость [Н/м] x — удлинение пружины [м] Потенциальная энергия Еп = mgh Еп — потенциальная энергия [Дж] m — масса тела [кг] g — ускорение свободного падения [м/с^2] На планете Земля g ≃ 9,8 м/с^2 Задачка раз Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2. Решение: Формула потенциальной энергии Еп = mgh Eп = 0,1 * 9,8 * 2500=2450 Дж Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж. Задачка два Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2. Решение: Формула потенциальной энергии Еп = mgh Переведем 637 кДж в Джоули. 637 кДж = 637000 Дж h = 637 000/(65 * 9,8) = 1000 м Ответ: высота горы равна 1000 метров. Задачка три Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола. Решение: Потенциальная энергия вычисляется по формуле: E = mgh По условию задачи Таким образом, получим, что E1 = m*g*2h = 2 mgh, Ответ: E1 = E2. В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии. Закон сохранения энергии Полная механическая энергия замкнутой системы остается постоянной. Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так: Закон сохранения энергии Еполн.мех. = Еп + Eк = const Еполн.мех. — полная механическая энергия системы [Дж] Еп — потенциальная энергия [Дж] Ек — кинетическая энергия [Дж] const — постоянная величина Задачка раз Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза? Решение: Должен выполняться закон сохранения энергии: В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна. В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты. Это можно описать соотношением: Еп1 + Ек1 = Еп2 + Ек2 Разделим на массу левую и правую часть Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза. Ответ: высота увеличится в 4 раза Задачка два Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h? Решение По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0. Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0. Ответ: Емех = mgh0. Задачка три Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь. Решение: Переведем массу из граммов в килограммы: m = 100 г = 0,1 кг У поверхности земли полная механическая энергия мяча равна его кинетической энергии: Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии: mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж h = E/mg = 1,6/0,1*10 = 1,6 м Ответ: мяч имел скорость 2 м/с на высоте 1,6 м Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров. Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться. Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю. Задачка Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце? Решение: В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек. В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2 Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр Емех = Емех/2 + Евнутр Ответ: во внутреннюю перейдет половина начальной кинетической энергии Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую. Вот что сформулировал Фурье: При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия. Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы. Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры. Закон сохранения энергии в тепловых процессах При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом. Математически его можно описать так: Уравнение теплового баланса Q отд = Q пол Qотд — отданное системой количество теплоты [Дж] Q пол — полученное системой количество теплоты [Дж] Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом: Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен. Задачка раз Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии. Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С). Решение: При нагревании тело получает количество теплоты где c — удельная теплоемкость вещества При сгорании тела выделяется энергия где q — удельная теплота сгорания топлива По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии. cmΔt =0,2 * qmсгор mсгор = cmΔt / 0,2 q Ответ: масса сгоревшего топливаа равна 33,6 г. Задачка два Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг. Решение: Для нагревания льда до температуры плавления необходимо: Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж Для превращения льда в воду: Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла. Источникп.7. Задачи
Сила, удерживающая пружину в растянутом состоянии, должна уравновешивать силу упругости, т.е. быть равной ей по величине \(F=F_\text<упр>=kx\). По направлению эти силы противоположны: удерживающая сила растягивает пружину, сила упругости стремится вернуть её в исходное состояние.
Следовательно, жесткость пружины: \begin
При подъеме на высоту \(h\) ведро массу не меняет и приобретает потенциальную энергию \begin
Работа сторонних сил (силы тяги) по преодолению силы тяжести \(A_\text<в>=-A’_\text<в>=Mgh\). Работа положительна, т.к. сила тяги направлена вверх.
С цепью немного сложней, т.к. масса цепи меняется при подъеме: в начале подъема она максимальна и равна \(m=8\ \text<кг>\), в конце подъема – минимальна и равна \(m_0=0\ \text<кг>\).
При равномерном подъеме средняя масса \begin Закон сохранения механической энергии
Энергия: что это такое
Механическая энергия
Кинетическая энергия
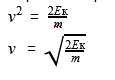
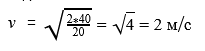
Потенциальная энергия

Закон сохранения энергии
Переход механической энергии во внутреннюю
Закон сохранения энергии в тепловых процессах